Thermomechanische Analyse: Unterschied zwischen den Versionen
| (20 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | < | + | {{PSM_Infobox}} |
| − | + | <span style="font-size:1.2em;font-weight:bold;">Thermomechanische Analyse (TMA)</span> | |
| − | Mit zunehmender Beanspruchungstemperatur erfahren | + | __FORCETOC__ |
| − | Der Wärmeausdehnungskoeffizient <math>\alpha</math>, auch als Wärmedehnzahl bezeichnet, beschreibt die Längenänderung L<sub>1</sub> bzw. Volumenänderung V<sub>1</sub> eines Körpers bei 1 K Temperaturerhöhung und wird in K<sup>-1</sup> angegeben [1]. | + | ==Grundlagen der Wärmeausdehnung== |
| + | Mit zunehmender Beanspruchungstemperatur erfahren [[polymer]]e Werkstoffe eine Längenausdehnung. Die Messung der Wärmeausdehnung liefert Informationen über den mittleren linearen (<math>\alpha</math>) bzw. den kubischen (<math>\beta</math>) Wärmeausdehnungskoeffizienten des jeweiligen [[Kunststoffe]]s sowie über wichtige Umwandlungserscheinungen beim Erwärmen.<br> | ||
| + | Der [[Thermischer Ausdehnungskoeffizient|Wärmeausdehnungskoeffizient]] <math>\alpha</math>, auch als Wärmedehnzahl bezeichnet, beschreibt die Längenänderung L<sub>1</sub> bzw. Volumenänderung V<sub>1</sub> eines Körpers bei 1 K Temperaturerhöhung und wird in K<sup>-1</sup> angegeben [1]. | ||
In einem begrenzten Temperaturintervall ergibt sich für die lineare Längenausdehnung | In einem begrenzten Temperaturintervall ergibt sich für die lineare Längenausdehnung | ||
{| | {| | ||
| − | |||
| − | |||
|- | |- | ||
| + | |width="20px"| | ||
| + | |width="500px" | <math>L_1\,=\,L_0\,+\,\alpha\,L_0\,\left(T_1\,-\,T_0\right)</math> | ||
| + | |(1) | ||
|} | |} | ||
| + | |||
und für die räumliche Volumenausdehnung | und für die räumliche Volumenausdehnung | ||
{| | {| | ||
| − | |||
| − | |||
|- | |- | ||
| + | |width="20px"| | ||
| + | |width="500px" | <math>V_1\,=\,V_0\,+\,\beta\,V_0\,\left(T_1\,-\,T_0\right)</math> | ||
| + | |(2) | ||
|} | |} | ||
wobei für den isotropen Körper die Beziehung | wobei für den isotropen Körper die Beziehung | ||
{| | {| | ||
| − | |||
| − | |||
|- | |- | ||
| + | |width="20px"| | ||
| + | |width="500px" | <math>\beta\,=\,3\,\alpha</math> | ||
| + | |(3) | ||
|} | |} | ||
| Zeile 26: | Zeile 32: | ||
Auf Grund der Temperaturabhängigkeit des Koeffizienten <math>\alpha</math> bzw. <math>\beta</math> ist jedoch mit nichtlinearen Abhängigkeiten zu rechnen und es gilt | Auf Grund der Temperaturabhängigkeit des Koeffizienten <math>\alpha</math> bzw. <math>\beta</math> ist jedoch mit nichtlinearen Abhängigkeiten zu rechnen und es gilt | ||
{| | {| | ||
| − | |||
| − | |||
|- | |- | ||
| + | |width="20px"| | ||
| + | |width="500px" | <math>\alpha\,=\,\frac{1}{L_0}\,\left( \frac{\delta\,L}{\delta\,T}\right)_p</math> bzw. <math>\beta\,=\,\frac{1}{V_0}\,\left( \frac{\delta\,V}{\delta\,T}\right)_p</math> | ||
| + | |(4) | ||
|} | |} | ||
| − | Die Nichtlinearität ist eine Folge der mit steigender Temperatur einsetzenden lokalen Bewegung kleiner Molekülgruppen (Nebenrelaxation) und der danach einsetzenden kooperativen Bewegungen ganzer Molekülteile (Hauptrelaxationen). In Umwandlungsgebieten ändern sich die Ausdehnungskoeffizienten sprunghaft. | + | Die Nichtlinearität ist eine Folge der mit steigender Temperatur einsetzenden lokalen Bewegung kleiner Molekülgruppen (Nebenrelaxation) und der danach einsetzenden kooperativen Bewegungen ganzer Molekülteile (Hauptrelaxationen). In den Umwandlungsgebieten ändern sich die Ausdehnungskoeffizienten sprunghaft. |
| − | Die Bestimmung der Ausdehnungskoeffizienten ist auf Temperaturbereiche beschränkt, in denen die Wärmeausdehnung nahezu temperaturunabhängig ist. Daraus ergibt sich eine hohe Anforderung an die Empfindlichkeit der Längenmesstechnik. Exakte Kennwerte ergeben sich dabei nur im festen Zustand des zu charakterisierenden | + | |
| − | + | ==Verfahren der Längenmesstechnik== | |
| + | |||
| + | Die Bestimmung der [[Thermischer Ausdehnungskoeffizient|Ausdehnungskoeffizienten]] ist auf Temperaturbereiche beschränkt, in denen die Wärmeausdehnung nahezu temperaturunabhängig ist. Daraus ergibt sich eine hohe Anforderung an die Empfindlichkeit der [[Zugversuch#Zugversuch, Wegmesstechnik|Längenmesstechnik]]. Exakte [[Werkstoffkennwert|Kennwerte]] ergeben sich dabei nur im festen Zustand des zu charakterisierenden [[Kunststoffe]]s, da bei der Ermittlung das Ergebnis durch eine Reihe von wesentlichen Faktoren beeinflusst wird. [[Polymer]]werkstoffe sind mehr oder weniger hygroskopisch oder enthalten flüchtige Bestandteile, die bei äußerer Wärmezuführung zu [[Schwindung]] und Austrocknung neigen und der Wärmedehnung entgegenwirken. Deshalb sollten Verfahren angewendet werden, die Nebeneinflüsse ausschalten, jedoch den Bedingungen des praktischen Einsatzes entsprechen. Bei optischen Ausdehnungsmessgeräten erfolgt die Ausdehnungsmessung visuell durch ein Messmikroskop. Als Messmarkierung klebt man auf den Prüfköper Blattzinnstreifen auf. Die Erwärmung der [[Prüfkörper]] erfolgt in heißer Luft mittels geeigneten Heiztischs. Über einen speziellen Regelkreis sind die Thermosensoren bzw. störenden Sollwertpendlungen zu kontrollieren und zu unterdrücken. Der Temperaturanstieg sollte in der Größenordnung von 5 K h<sup>-1</sup> liegen. Geringste Krümmungen oder [[Schrumpfversuch|Schrumpfungen]] des Prüfkörpers bei Annäherung an den Erweichungsbereich können das Ergebnis verfälschen. Bei Messungen mit dem Quarzrohrdilatometer wird die Längenänderung nach einer Temperatur T über eine Messuhr oder einen induktiven Wegaufnehmer erfasst. Damit tritt eine Verformungsbehinderung auf, die gegen die Ausdehnung wirkt. Die Erwärmung kann in Luft oder im Flüssigkeitsbad erfolgen, wobei eine [[Messgenauigkeit|Genauigkeit]] von 0,2 K für die einzelnen Stufen anzustreben ist. Verdrängungsdilatometer stellen im Prinzip Pyknometer dar, in denen die Änderung der Standhöhe der Flüssigkeit durch Erwärmen eines Messraumes, in dem sich der Prüfkörper befindet, an einer kalibrierten Kapillare abgelesen wird. Als Messflüssigkeiten haben sich Quecksilber und Methanol bewährt. Die Erwärmung des Messraumes erfolgt im Flüssigkeitsbad, wobei ebenfalls eine [[Messgenauigkeit|Genauigkeit]] von 0,2 K vorliegt. Diese Methode ist geeignet, die Volumenausdehnung direkt, ohne Unterbrechung bis in den Flüssigkeitsbereich zu messen. Der interessierende Temperaturbereich wird in kleinen Schritten durchfahren. | ||
| + | |||
| + | ==Experimentelle Durchführung der TMA== | ||
| + | Für Kunststoffe hat sich zur Messung des linearen [[Thermischer Ausdehnungskoeffizient|thermischen Ausdehnungskoeffizienten]] die Thermomechanische Analyse (TMA) bewährt. Im Gegensatz zum kraftfreien Dilatometerverfahren wird bei der TMA mit einer konstanten, geringen Auflast gemessen. Zum Einsatz kommen zylindrische oder quaderförmige Prüfkörper mit planparallelen Messflächen. Über einen Quarzstempel erfolgt die Aufbringung der geringen Last (0,1 bis 5 g) und gleichzeitig über ein induktives Messsystem die Messung der Wärmeausdehnung. Der Versuchsaufbau befindet sich in einem Ofen, der mit geringer Heizrate aufgeheizt wird. Auf der Grundlage der DIN 53752 [2] bzw. ISO 11359 [3] können ein mittlerer (Gl. 5) oder ein differentieller thermischer Längenausdehnungskoeffizient (Gl. 6) ermittelt werden. | ||
{| | {| | ||
| − | |||
| − | |||
|- | |- | ||
| + | |width="20px"| | ||
| + | |width="500px" | <math>\bar \alpha\left(T\right)\,=\,\frac{1}{L_0}\,\cdot\, \frac{L_2\,-\,L_1}{T_2\,-\,T_1}\,=\, \frac{1}{L_0}\,\cdot\, \frac{\Delta L}{\Delta T}</math> | ||
| + | |(5) | ||
|} | |} | ||
{| | {| | ||
| − | |||
| − | |||
|- | |- | ||
| + | |width="20px"| | ||
| + | |width="500px" | <math>\alpha\left(T\right)\,=\,\frac{1}{L_0}\,\cdot\, \frac{dL}{dT}</math> | ||
| + | |(6) | ||
|} | |} | ||
| − | Der differentielle thermische Längenausdehungskoeffizient wird durch den Anstieg der Tangente an die Abhängigkeit | + | Der differentielle thermische Längenausdehungskoeffizient wird durch den Anstieg der Tangente an die Abhängigkeit <math>\Delta</math>L/L<sub>0</sub> bestimmt. Er ist zu Beginn des Versuches immer „0“. Ebenso wie bei der [[Differential Scanning Calorimetry]] (DSC) liefert die erste Heizlauf einer TMA immer Informationen zur thermischen und mechanischen Vorgeschichte. Durch die Erwärmung können nicht nur flüchtige Bestandteile entweichen, es kann auch zum Abbau von [[Zugversuch Eigenspannungen Orientierungen|Orientierungen und Eigenspannung]] kommen und es können Nachkristallisationsprozesse einsetzen. Alle diese Prozesse sind mit einer [[Schrumpfung]] verbunden und wirken der Wärmeausdehnung entgegen. In [[Duroplaste|Duromeren]] bewirken Nachhärtungsprozesse den gleichen Effekt. Außerdem sind in Spritzguss- und Extrusionsteilen [[Anisotropie]]effekte zu berücksichtigen. Dies gilt auch für [[Teilchengefüllte Kunststoffe|gefüllte]] und [[Faserverstärkte Kunststoffe|verstärkte Kunststoffe]].<br> |
| − | erste Heizlauf einer TMA immer Informationen zur thermischen und mechanischen Vorgeschichte. Durch die Erwärmung können nicht nur flüchtige Bestandteile entweichen, es kann auch zum Abbau von Orientierungen und Eigenspannung kommen und es können Nachkristallisationsprozesse einsetzen. Alle diese Prozesse sind mit einer Schrumpfung verbunden und wirken der Wärmeausdehnung entgegen. In Duromeren bewirken Nachhärtungsprozesse den gleichen Effekt. Außerdem sind in Spritzguss- und Extrusionsteilen | + | Bei teilkristallinen [[Polymer]]en tritt beim Erwärmen eine mehr oder weniger ausgeprägte Kontraktion auf, der lineare [[Thermischer Ausdehnungskoeffizient|Ausdehnungskoeffizient]] in Kettenrichtung kann negative Werte annehmen. Die Ursache liegt in der ungestörten [[Gummielastizität|gummielastischen]] Rückstellung der tie-Moleküle [4] in den amorphen Bereichen. Da eine Volumenmessung positive Werte liefert, muss senkrecht zur Orientierungsrichtung ein entsprechend stärkerer Anstieg des Ausdehnungskoeffizienten vorliegen. Für Polyethylen ([[Kurzzeichen]]: PE) wurde bei Raumtemperatur für <math>\alpha</math><sub>||</sub>= - 2,4•10<sup>-5</sup> K<sup>-1</sup> und <math>\alpha</math><sub>⊥</sub> = 19•10<sup>-5</sup> K<sup>-1</sup> gefunden. Umgekehrt sollte es demzufolge möglich sein, durch Messung der Richtungsabhängigkeit des linearen Ausdehnungskoeffizienten Aussagen über den Orientierungszustand zu erhalten [5].<br> |
| − | Bei teilkristallinen | + | Analog zu den teilkristallinen Polymeren hängt die Wärmedehnzahl bei den amorphen mehrphasigen Systemen erwartungsgemäß vom Anteil der Komponenten und der Verträglichkeit der Phasen ab. Oberhalb der [[Glastemperatur]] beider Komponenten folgt der Ausdehnungskoeffizient meist einem einfachen Additivgesetz. Im Bereich zwischen den Glasumwandlungstemperaturen der beteiligten [[Polymer]]e gilt dies nur noch teilweise. Darüber hinaus kann das unterschiedliche Ausdehnungsverhalten der Phasen zur Ausbildung von thermisch induzierten Spannungen ([[Zugversuch_Eigenspannungen_Orientierungen#Eigenspannung|Eigenspannungen]]) führen, welche die Makroeigenschaften des [[Polymer]]blends negativ beeinflussen. |
| − | Analog zu den teilkristallinen Polymeren hängt die Wärmedehnzahl bei den | ||
| − | Bereich zwischen den Glasumwandlungstemperaturen der beteiligten | ||
| − | |||
| − | + | ==Anwendungsbeispiel== | |
| − | |||
| + | Verbundsysteme von Kunststoffen mit anorganischen Füllstoffen zeigen in Abhängigkeit vom Füllstoffanteil, der Partikelform und dem herstellungsbedingten Ordnungszustand i. Allg. eine geringere Wärmeausdehnung, da sich der Matrixwerkstoff stärker ausdehnt als die Füllstoffe. Infolgedessen sind auch die zu erwartenden inneren Spannungen, insbesondere an den [[Phasengrenzfläche|Grenzflächen]] Polymer/Füllstoff ausgeprägter. Der Anwendung der Mischungsregel zur analytischen Bewertung des Ausdehnungskoeffizienten eines Verbundes sind Grenzen gesetzt. Solange die Bestimmungsgleichungen die Wechselwirkung Matrix-Füllstoffoberfläche, Veränderungen des freien Volumens, Perkolationseffekte und Teilchengröße nicht erfassen, können nur Richtwerte angegeben werden. | ||
| + | [[Datei:Thermomechanische Analyse.JPG]] | ||
| + | {| | ||
| + | |- valign="top" | ||
| + | |width="50px"|'''Bild 1''': | ||
| + | |width="600px" |Wärmeausdehnungsverhalten einer faserverstärkten Polyphenylensulfid ([[Kurzzeichen]]: PPS)-Platte in Radial-, Tangential und Dickenrichtung | ||
| + | |} | ||
| − | Der Einfluss einer Faserverstärkung auf das Wärmeausdehnungsverhalten einer kreisrunden Platte zeigt das Bild. Während sich in Radial- und Tangentialrichtung nur geringe Unterscheide im Wärmeausdehnungsverhalten ergeben, ist in | + | Der Einfluss einer [[Faserverstärkte Kunststoffe#Arten von Verstärkungsfasern|Faserverstärkung]] auf das Wärmeausdehnungsverhalten einer kreisrunden Platte zeigt das '''Bild 1'''. Während sich in Radial- und Tangentialrichtung nur geringe Unterscheide im Wärmeausdehnungsverhalten ergeben, ist in Dickenrichtung eine deutlich stärkere Wärmeausdehnung nachweisbar, die wesentlich durch das Wärmeausdehnungsverhalten der unverstärkten Matrix bestimmt wird. Aus der [[Anisotropie]] des Wärmeausdehnungsverhaltens können Schlussfolgerungen zur [[Faserorientierung]] abgeleitet werden.<br> |
| − | Ein wesentlicher Beitrag der Entstehung von inneren Spannungen resultiert aus dem Wärmeausdehnungsverhalten. Des Weiteren ist in diesem Zusammenhang zu | + | Ein wesentlicher Beitrag der Entstehung von inneren Spannungen resultiert aus dem Wärmeausdehnungsverhalten. Des Weiteren ist in diesem Zusammenhang zu berücksichtigen, dass der Wärmeausdehnungskoeffizient (siehe: [[Thermischer Ausdehnungskoeffizient]]) mit zunehmendem [[Elastizitätsmodul|E-Modul]] abnimmt. Eine Behinderung der thermischen Ausdehnung führt zu einem Spannungsaufbau im Werkstoff, zu so genannten Wärmespannungen. Dies gilt sowohl für den Fall der kraftschlüssigen Kombination von Werkstoffen unterschiedlicher thermischer und elastischer Eigenschaften als auch für den Fall unterschiedlicher Temperaturen in einem Erzeugnis. Im Werkstoff bzw. Werkstoffbereichen mit dem geringeren Wärmeausdehnungskoeffizienten bauen sich Zugspannungen, in den anderen Druckspannungen auf. Entfallen die Ursachen der Wärmespannungen, verschwinden die inneren Spannungen unter der Voraussetzung dass keine [[Deformation#Plastische Deformation|plastischen Deformationen]] auftreten vollständig. Andernfalls kommt es zur Entstehung von [[Zugversuch Eigenspannungen Orientierungen|Eigenspannungen]]. |
| − | berücksichtigen, dass Wärmeausdehnungskoeffizient mit zunehmendem E-Modul abnimmt. Eine Behinderung der thermischen Ausdehnung führt zu einem | ||
| − | thermischer und elastischer Eigenschaften als auch für den Fall unterschiedlicher Temperaturen in einem Erzeugnis. Im Werkstoff bzw. Werkstoffbereichen mit dem geringeren Wärmeausdehnungskoeffizienten bauen sich Zugspannungen, in den anderen Druckspannungen auf. Entfallen die Ursachen der Wärmespannungen, | ||
| − | verschwinden die inneren Spannungen unter der Voraussetzung dass keine | ||
| + | '''Literaturhinweise''' | ||
| + | {| | ||
| + | |-valign="top" | ||
| + | |[1] | ||
| + | |[[Grellmann,_Wolfgang|Grellmann, W.]], [[Seidler,_Sabine|Seidler, S.]] (Hrsg.): Kunststoffprüfung. Carl Hanser Verlag, München (2015) 3. Auflage, S. 319 ff, (ISBN 978-3-446-44350-1; siehe [[AMK-Büchersammlung]] unter A 18) | ||
| + | |-valign="top" | ||
| + | |[2] | ||
| + | |DIN 53752 (1980-12): Prüfung von Kunststoffen – Bestimmung des thermischen Längenausdehnungskoeffizienten (zurückgezogen; ersetzt durch ISO 11359) | ||
| + | |-valign="top" | ||
| + | |[3] | ||
| + | |ISO 11359: Kunststoffe – Thermomechanische Analyse (TMA) | ||
| + | |- | ||
| + | | | ||
| + | |Teil 1 (2023-02): Allgemeine Grundlagen | ||
| + | |- | ||
| + | | | ||
| + | |Teil 2 (2021-11): Bestimmung des linearen thermischen Ausdehnungskoeffizienten und der Glasübergangstemperatur | ||
| + | |- | ||
| + | | | ||
| + | |-valign="top" | ||
| + | |[4] | ||
| + | |[[Michler,_Goerg_Hannes|Michler, G. H.]]: Kunststoff-Mikromechanik – Morphologie, Deformations- und Bruchmechanismen. Carl Hanser Verlag, München Wien (1992), (ISBN 3-446-17068-5; siehe [[AMK-Büchersammlung]] unter F 4) | ||
| + | |-valign="top" | ||
| + | |[5] | ||
| + | |Schmiedel, H. (Hrsg.): Handbuch der Kunststoffprüfung. Carl Hanser Verlag, München Wien (1992), (ISBN 3-446-16336-0; siehe [[AMK-Büchersammlung]] unter A 3) | ||
| + | |} | ||
| − | + | [[Kategorie:Thermoanalytische Methoden]] | |
| − | |||
| − | [ | ||
| − | |||
| − | [ | ||
| − | |||
| − | |||
| − | |||
| − | |||
Aktuelle Version vom 4. August 2023, 12:14 Uhr
| Ein Service der |
|---|

|
| Polymer Service GmbH Merseburg |
| Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de |
| Unser Weiterbildungsangebot: https://www.psm-merseburg.de/weiterbildung |
| PSM bei Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg |
Thermomechanische Analyse (TMA)
Grundlagen der Wärmeausdehnung
Mit zunehmender Beanspruchungstemperatur erfahren polymere Werkstoffe eine Längenausdehnung. Die Messung der Wärmeausdehnung liefert Informationen über den mittleren linearen () bzw. den kubischen () Wärmeausdehnungskoeffizienten des jeweiligen Kunststoffes sowie über wichtige Umwandlungserscheinungen beim Erwärmen.
Der Wärmeausdehnungskoeffizient , auch als Wärmedehnzahl bezeichnet, beschreibt die Längenänderung L1 bzw. Volumenänderung V1 eines Körpers bei 1 K Temperaturerhöhung und wird in K-1 angegeben [1].
In einem begrenzten Temperaturintervall ergibt sich für die lineare Längenausdehnung
| (1) |
und für die räumliche Volumenausdehnung
| (2) |
wobei für den isotropen Körper die Beziehung
| (3) |
gilt.
Auf Grund der Temperaturabhängigkeit des Koeffizienten bzw. ist jedoch mit nichtlinearen Abhängigkeiten zu rechnen und es gilt
| bzw. | (4) |
Die Nichtlinearität ist eine Folge der mit steigender Temperatur einsetzenden lokalen Bewegung kleiner Molekülgruppen (Nebenrelaxation) und der danach einsetzenden kooperativen Bewegungen ganzer Molekülteile (Hauptrelaxationen). In den Umwandlungsgebieten ändern sich die Ausdehnungskoeffizienten sprunghaft.
Verfahren der Längenmesstechnik
Die Bestimmung der Ausdehnungskoeffizienten ist auf Temperaturbereiche beschränkt, in denen die Wärmeausdehnung nahezu temperaturunabhängig ist. Daraus ergibt sich eine hohe Anforderung an die Empfindlichkeit der Längenmesstechnik. Exakte Kennwerte ergeben sich dabei nur im festen Zustand des zu charakterisierenden Kunststoffes, da bei der Ermittlung das Ergebnis durch eine Reihe von wesentlichen Faktoren beeinflusst wird. Polymerwerkstoffe sind mehr oder weniger hygroskopisch oder enthalten flüchtige Bestandteile, die bei äußerer Wärmezuführung zu Schwindung und Austrocknung neigen und der Wärmedehnung entgegenwirken. Deshalb sollten Verfahren angewendet werden, die Nebeneinflüsse ausschalten, jedoch den Bedingungen des praktischen Einsatzes entsprechen. Bei optischen Ausdehnungsmessgeräten erfolgt die Ausdehnungsmessung visuell durch ein Messmikroskop. Als Messmarkierung klebt man auf den Prüfköper Blattzinnstreifen auf. Die Erwärmung der Prüfkörper erfolgt in heißer Luft mittels geeigneten Heiztischs. Über einen speziellen Regelkreis sind die Thermosensoren bzw. störenden Sollwertpendlungen zu kontrollieren und zu unterdrücken. Der Temperaturanstieg sollte in der Größenordnung von 5 K h-1 liegen. Geringste Krümmungen oder Schrumpfungen des Prüfkörpers bei Annäherung an den Erweichungsbereich können das Ergebnis verfälschen. Bei Messungen mit dem Quarzrohrdilatometer wird die Längenänderung nach einer Temperatur T über eine Messuhr oder einen induktiven Wegaufnehmer erfasst. Damit tritt eine Verformungsbehinderung auf, die gegen die Ausdehnung wirkt. Die Erwärmung kann in Luft oder im Flüssigkeitsbad erfolgen, wobei eine Genauigkeit von 0,2 K für die einzelnen Stufen anzustreben ist. Verdrängungsdilatometer stellen im Prinzip Pyknometer dar, in denen die Änderung der Standhöhe der Flüssigkeit durch Erwärmen eines Messraumes, in dem sich der Prüfkörper befindet, an einer kalibrierten Kapillare abgelesen wird. Als Messflüssigkeiten haben sich Quecksilber und Methanol bewährt. Die Erwärmung des Messraumes erfolgt im Flüssigkeitsbad, wobei ebenfalls eine Genauigkeit von 0,2 K vorliegt. Diese Methode ist geeignet, die Volumenausdehnung direkt, ohne Unterbrechung bis in den Flüssigkeitsbereich zu messen. Der interessierende Temperaturbereich wird in kleinen Schritten durchfahren.
Experimentelle Durchführung der TMA
Für Kunststoffe hat sich zur Messung des linearen thermischen Ausdehnungskoeffizienten die Thermomechanische Analyse (TMA) bewährt. Im Gegensatz zum kraftfreien Dilatometerverfahren wird bei der TMA mit einer konstanten, geringen Auflast gemessen. Zum Einsatz kommen zylindrische oder quaderförmige Prüfkörper mit planparallelen Messflächen. Über einen Quarzstempel erfolgt die Aufbringung der geringen Last (0,1 bis 5 g) und gleichzeitig über ein induktives Messsystem die Messung der Wärmeausdehnung. Der Versuchsaufbau befindet sich in einem Ofen, der mit geringer Heizrate aufgeheizt wird. Auf der Grundlage der DIN 53752 [2] bzw. ISO 11359 [3] können ein mittlerer (Gl. 5) oder ein differentieller thermischer Längenausdehnungskoeffizient (Gl. 6) ermittelt werden.
| (5) |
| (6) |
Der differentielle thermische Längenausdehungskoeffizient wird durch den Anstieg der Tangente an die Abhängigkeit L/L0 bestimmt. Er ist zu Beginn des Versuches immer „0“. Ebenso wie bei der Differential Scanning Calorimetry (DSC) liefert die erste Heizlauf einer TMA immer Informationen zur thermischen und mechanischen Vorgeschichte. Durch die Erwärmung können nicht nur flüchtige Bestandteile entweichen, es kann auch zum Abbau von Orientierungen und Eigenspannung kommen und es können Nachkristallisationsprozesse einsetzen. Alle diese Prozesse sind mit einer Schrumpfung verbunden und wirken der Wärmeausdehnung entgegen. In Duromeren bewirken Nachhärtungsprozesse den gleichen Effekt. Außerdem sind in Spritzguss- und Extrusionsteilen Anisotropieeffekte zu berücksichtigen. Dies gilt auch für gefüllte und verstärkte Kunststoffe.
Bei teilkristallinen Polymeren tritt beim Erwärmen eine mehr oder weniger ausgeprägte Kontraktion auf, der lineare Ausdehnungskoeffizient in Kettenrichtung kann negative Werte annehmen. Die Ursache liegt in der ungestörten gummielastischen Rückstellung der tie-Moleküle [4] in den amorphen Bereichen. Da eine Volumenmessung positive Werte liefert, muss senkrecht zur Orientierungsrichtung ein entsprechend stärkerer Anstieg des Ausdehnungskoeffizienten vorliegen. Für Polyethylen (Kurzzeichen: PE) wurde bei Raumtemperatur für ||= - 2,4•10-5 K-1 und ⊥ = 19•10-5 K-1 gefunden. Umgekehrt sollte es demzufolge möglich sein, durch Messung der Richtungsabhängigkeit des linearen Ausdehnungskoeffizienten Aussagen über den Orientierungszustand zu erhalten [5].
Analog zu den teilkristallinen Polymeren hängt die Wärmedehnzahl bei den amorphen mehrphasigen Systemen erwartungsgemäß vom Anteil der Komponenten und der Verträglichkeit der Phasen ab. Oberhalb der Glastemperatur beider Komponenten folgt der Ausdehnungskoeffizient meist einem einfachen Additivgesetz. Im Bereich zwischen den Glasumwandlungstemperaturen der beteiligten Polymere gilt dies nur noch teilweise. Darüber hinaus kann das unterschiedliche Ausdehnungsverhalten der Phasen zur Ausbildung von thermisch induzierten Spannungen (Eigenspannungen) führen, welche die Makroeigenschaften des Polymerblends negativ beeinflussen.
Anwendungsbeispiel
Verbundsysteme von Kunststoffen mit anorganischen Füllstoffen zeigen in Abhängigkeit vom Füllstoffanteil, der Partikelform und dem herstellungsbedingten Ordnungszustand i. Allg. eine geringere Wärmeausdehnung, da sich der Matrixwerkstoff stärker ausdehnt als die Füllstoffe. Infolgedessen sind auch die zu erwartenden inneren Spannungen, insbesondere an den Grenzflächen Polymer/Füllstoff ausgeprägter. Der Anwendung der Mischungsregel zur analytischen Bewertung des Ausdehnungskoeffizienten eines Verbundes sind Grenzen gesetzt. Solange die Bestimmungsgleichungen die Wechselwirkung Matrix-Füllstoffoberfläche, Veränderungen des freien Volumens, Perkolationseffekte und Teilchengröße nicht erfassen, können nur Richtwerte angegeben werden.
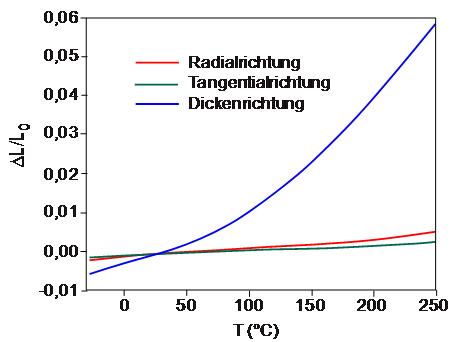
| Bild 1: | Wärmeausdehnungsverhalten einer faserverstärkten Polyphenylensulfid (Kurzzeichen: PPS)-Platte in Radial-, Tangential und Dickenrichtung |
Der Einfluss einer Faserverstärkung auf das Wärmeausdehnungsverhalten einer kreisrunden Platte zeigt das Bild 1. Während sich in Radial- und Tangentialrichtung nur geringe Unterscheide im Wärmeausdehnungsverhalten ergeben, ist in Dickenrichtung eine deutlich stärkere Wärmeausdehnung nachweisbar, die wesentlich durch das Wärmeausdehnungsverhalten der unverstärkten Matrix bestimmt wird. Aus der Anisotropie des Wärmeausdehnungsverhaltens können Schlussfolgerungen zur Faserorientierung abgeleitet werden.
Ein wesentlicher Beitrag der Entstehung von inneren Spannungen resultiert aus dem Wärmeausdehnungsverhalten. Des Weiteren ist in diesem Zusammenhang zu berücksichtigen, dass der Wärmeausdehnungskoeffizient (siehe: Thermischer Ausdehnungskoeffizient) mit zunehmendem E-Modul abnimmt. Eine Behinderung der thermischen Ausdehnung führt zu einem Spannungsaufbau im Werkstoff, zu so genannten Wärmespannungen. Dies gilt sowohl für den Fall der kraftschlüssigen Kombination von Werkstoffen unterschiedlicher thermischer und elastischer Eigenschaften als auch für den Fall unterschiedlicher Temperaturen in einem Erzeugnis. Im Werkstoff bzw. Werkstoffbereichen mit dem geringeren Wärmeausdehnungskoeffizienten bauen sich Zugspannungen, in den anderen Druckspannungen auf. Entfallen die Ursachen der Wärmespannungen, verschwinden die inneren Spannungen unter der Voraussetzung dass keine plastischen Deformationen auftreten vollständig. Andernfalls kommt es zur Entstehung von Eigenspannungen.
Literaturhinweise
| [1] | Grellmann, W., Seidler, S. (Hrsg.): Kunststoffprüfung. Carl Hanser Verlag, München (2015) 3. Auflage, S. 319 ff, (ISBN 978-3-446-44350-1; siehe AMK-Büchersammlung unter A 18) |
| [2] | DIN 53752 (1980-12): Prüfung von Kunststoffen – Bestimmung des thermischen Längenausdehnungskoeffizienten (zurückgezogen; ersetzt durch ISO 11359) |
| [3] | ISO 11359: Kunststoffe – Thermomechanische Analyse (TMA) |
| Teil 1 (2023-02): Allgemeine Grundlagen | |
| Teil 2 (2021-11): Bestimmung des linearen thermischen Ausdehnungskoeffizienten und der Glasübergangstemperatur | |
| [4] | Michler, G. H.: Kunststoff-Mikromechanik – Morphologie, Deformations- und Bruchmechanismen. Carl Hanser Verlag, München Wien (1992), (ISBN 3-446-17068-5; siehe AMK-Büchersammlung unter F 4) |
| [5] | Schmiedel, H. (Hrsg.): Handbuch der Kunststoffprüfung. Carl Hanser Verlag, München Wien (1992), (ISBN 3-446-16336-0; siehe AMK-Büchersammlung unter A 3) |