TABOR-Beziehung: Unterschied zwischen den Versionen
Die Seite wurde neu angelegt: „{{PSM_Infobox}} <span style="font-size:1.2em;font-weight:bold;">TABOR-Beziehung</span> __FORCETOC__ ==Grundlagen der TABOR-Beziehung== Die Kenntnis des Zusammenha…“ |
Keine Bearbeitungszusammenfassung |
||
| (4 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
__FORCETOC__ | __FORCETOC__ | ||
==Grundlagen der TABOR-Beziehung== | ==Grundlagen der TABOR-Beziehung== | ||
Die Kenntnis des Zusammenhanges zwischen [[Härte]] und anderen mechanischen [[Kenngröße]]n, z. B. [[Festigkeit]], [[Elastizitätsmodul|E-Modul]] und [[Zähigkeit]], ist sowohl aus prüftechnischer Sicht als auch für das Verständnis des makroskopischen Werkstoffverhaltens von außerordentlich praktischem Interesse. Auf experimenteller Basis gefundene empirische Zusammenhänge ermöglichen eine zeit- und kostensparende Qualitätsüberwachung von Werkstoffen und Bauteilen. Dabei ist jedoch zu beachten, dass diese empirischen Korrelationen nur innerhalb bestimmter Werkstoffklassen gültig sind. Aus der [[Härte]]prüfung metallischer Werkstoffe ist eine Abschätzung der [[Streckspannung|Fließspannung]] bzw. [[Streckspannung|Streckgrenze]] aus der Härte über die TABOR-Beziehung bekannt. Für ideal plastisches Werkstoffverhalten gilt lineare Proportionalität in der Form: | Die Kenntnis des Zusammenhanges zwischen [[Härte]] und anderen mechanischen [[Kenngröße]]n, z. B. [[Festigkeit]], [[Elastizitätsmodul|E-Modul]] und [[Zähigkeit]], ist sowohl aus prüftechnischer Sicht als auch für das Verständnis des makroskopischen Werkstoffverhaltens von außerordentlich praktischem Interesse. Auf experimenteller Basis gefundene empirische Zusammenhänge ermöglichen eine zeit- und kostensparende Qualitätsüberwachung von Werkstoffen und [[Bauteilprüfung|Bauteilen]]. Dabei ist jedoch zu beachten, dass diese empirischen Korrelationen nur innerhalb bestimmter Werkstoffklassen gültig sind. Aus der [[Härte]]prüfung metallischer Werkstoffe ist eine Abschätzung der [[Streckspannung|Fließspannung]] bzw. [[Streckspannung|Streckgrenze]] aus der Härte über die TABOR-Beziehung bekannt. Für ideal plastisches Werkstoffverhalten gilt lineare Proportionalität in der Form: | ||
{| | {| | ||
|- | |- | ||
| Zeile 33: | Zeile 33: | ||
Der Rückgriff auf solche Faustformeln sollte, wenn er überhaupt erfolgt, nach Möglichkeit von einigen Vor- oder Stichversuchen im konkreten Anwendungsfall begleitet werden. Durch Umwerten (siehe auch [[Härte|Härteumwertung]]) gewonnene [[Werkstoffkenngröße|Kenngrößen]] sind grundsätzlich als solche zu kennzeichnen. | Der Rückgriff auf solche Faustformeln sollte, wenn er überhaupt erfolgt, nach Möglichkeit von einigen Vor- oder Stichversuchen im konkreten Anwendungsfall begleitet werden. Durch Umwerten (siehe auch [[Härte|Härteumwertung]]) gewonnene [[Werkstoffkenngröße|Kenngrößen]] sind grundsätzlich als solche zu kennzeichnen. | ||
==Vickers-Härte/Streckspannung-Korrelation ausgewählter Kunststoffe== | ==Vickers-Härte/Streckspannung-Korrelation ausgewählter [[Kunststoffe]]== | ||
Die TABOR-Gleichung ist die grundlegende Beziehung für die Darstellung des Zusammenhanges zwischen [[Härte]] und [[Streckspannung|Streckgrenze]]. Von WEILER wurde für eine Vielzahl von [[Thermoplaste]]n der empirische Zusammenhang zwischen getrennt ermittelter [[Vickers-Härte]] und [[Streckspannung]] bei Zugbeanspruchung ermittelt ('''Bild 1'''). Für die im Bild angegebene Werkstoffpalette wird die Beziehung HV ≈ 2,33 σ<sub>y</sub> abgeleitet. | Die TABOR-Gleichung ist die grundlegende Beziehung für die Darstellung des Zusammenhanges zwischen [[Härte]] und [[Streckspannung|Streckgrenze]]. Von WEILER wurde für eine Vielzahl von [[Thermoplaste]]n der empirische Zusammenhang zwischen getrennt ermittelter [[Vickers-Härte]] und [[Streckspannung]] bei Zugbeanspruchung ermittelt ('''Bild 1'''). Für die im Bild angegebene Werkstoffpalette wird die Beziehung HV ≈ 2,33 σ<sub>y</sub> abgeleitet. | ||
| Zeile 44: | Zeile 44: | ||
|} | |} | ||
Bei der Betrachtung solcher Zusammenhänge müssen grundsätzlich methodische und werkstoffliche Aspekte berücksichtigt werden. Die Gleichung definiert den Zusammenhang zwischen Druckfließspannung (siehe [[Druckversuch]]) und [[Härte]], d. h. Korrelationen zwischen [[Streckspannung]]en aus dem [[Zugversuch]] und Härtewerten müssen zu Abweichungen von C = 3 führen, da durch das Auftreten einer hydrostatischen Komponente bei Druckbeanspruchung ein unterschiedliches [[Deformation]]sverhalten auftritt. Dies wird am Beispiel von Spannungs-Dehnungs- und Druckspannungs-Stauchungs-Kurven von Ethylen/Propylen ([[Kurzzeichen]]: E/P)-Copolymeren in '''Bild 2''' dargestellt. Die entsprechenden Streckspannungs- und Druckfließspannungswerte sind in '''Bild | Bei der Betrachtung solcher Zusammenhänge müssen grundsätzlich methodische und werkstoffliche Aspekte berücksichtigt werden. Die Gleichung definiert den Zusammenhang zwischen Druckfließspannung (siehe [[Druckversuch]]) und [[Härte]], d. h. Korrelationen zwischen [[Streckspannung]]en aus dem [[Zugversuch]] und Härtewerten müssen zu Abweichungen von C = 3 führen, da durch das Auftreten einer hydrostatischen Komponente bei Druckbeanspruchung ein unterschiedliches [[Deformation]]sverhalten auftritt. Dies wird am Beispiel von Spannungs-Dehnungs- und Druckspannungs-Stauchungs-Kurven von Ethylen/Propylen ([[Kurzzeichen]]: E/P)-Copolymeren in '''Bild 2''' dargestellt. Die entsprechenden Streckspannungs- und Druckfließspannungswerte sind in '''Bild 2c''' in Korrelation zur Eindringhärte dargestellt. Aus den funktionellen Zusammenhängen werden deutliche Unterschiede zwischen Zugbeanspruchung (H<sub>IT</sub> = 3,05 σ<sub>y</sub>) und Druckbeanspruchung (H<sub>IT</sub> = 1,75 σ<sub>y</sub>) ersichtlich, die in der Literatur auch für Polyethylen ([[Kurzzeichen]]: PE)-Werkstoffe gefunden werden. | ||
[[Datei:tabor_bild1.jpg|500px]] | [[Datei:tabor_bild1.jpg|500px]] | ||
| Zeile 95: | Zeile 95: | ||
'''Literaturhinweise''' | '''Literaturhinweise''' | ||
* Weiler, W. W.: Härteprüfung an Metallen und Kunststoffen. Expert Verlag, Renningen ( | * Weiler, W. W., Leeb, D., Müller, K., Rupp, D. M.: Härteprüfung an Metallen und Kunststoffen. Expert Verlag, Renningen (1985) (ISBN 3-8169-0013-5; siehe [[AMK-Büchersammlung]] unter M 25) | ||
* Baltá-Calleja, F. J., Fakirov, S.: Microhardness of Polymers. Cambridge University Press (2000) | * Baltá-Calleja, F. J., Fakirov, S.: Microhardness of Polymers. Cambridge University Press (2000) (ISBN 978-0-5216-4218-7) | ||
* Koch, T.: Morphologie und Mikrohärte von Polypropylen-Werkstoffen. Dissertation, Technische Universität Wien (2003), Mensch & Buchverlag (2005), (ISBN 3-89820-854-0; siehe [[AMK-Büchersammlung]] unter C 30) | * Koch, T.: Morphologie und Mikrohärte von Polypropylen-Werkstoffen. Dissertation, Technische Universität Wien (2003), Mensch & Buchverlag (2005), (ISBN 3-89820-854-0; siehe [[AMK-Büchersammlung]] unter C 30) | ||
* Tabor, D.: The Hardness of Metals. Oxford, Clarendon Press (1951) | * Tabor, D.: The Hardness of Metals. Oxford, Clarendon Press (1951) (ISBN 978-0-1985-0776-5) | ||
* Studman, C. J., Moore, M. A., Jones, S. E.: On the Correlation of Indentation Experiments. J. Phys. D: Appl. Phys. 10 (1977) 949–956 | * Studman, C. J., Moore, M. A., Jones, S. E.: On the Correlation of Indentation Experiments. J. Phys. D: Appl. Phys. 10 (1977) 949–956 | ||
* Johnson, K. L.: The Correlation of Indentation Experiments. J. Mech. Phys. Solids 18 (1970) 115–126 | * Johnson, K. L.: The Correlation of Indentation Experiments. J. Mech. Phys. Solids 18 (1970) 115–126 | ||
* May, M., Fröhlich, F., Grau, P., Grellmann, W.: Anwendung der Methode der registrierenden Mikrohärteprüfung für die Ermittlung von mechanischen Materialkennwerten an Polymerwerkstoffen. Plaste Kautschuk 30 (1983) 149–153 | * May, M., Fröhlich, F., Grau, P., [[Grellmann,_Wolfgang|Grellmann, W.]]: Anwendung der Methode der registrierenden Mikrohärteprüfung für die Ermittlung von mechanischen Materialkennwerten an Polymerwerkstoffen. Plaste Kautschuk 30 (1983) 149–153 [https://www.polymerservice-merseburg.de/fileadmin/inhalte/psm/veroeffentlichungen/May_Anwendung_der_registrierenden_Mikrohaertepruefung.pdf Download als pdf] | ||
[[Kategorie:Härte]] | [[Kategorie:Härte]] | ||
[[Kategorie:Instrumentierter Kerbschlagbiegeversuch]] | [[Kategorie:Instrumentierter Kerbschlagbiegeversuch]] | ||
Aktuelle Version vom 10. Juli 2024, 09:27 Uhr
| Ein Service der |
|---|

|
| Polymer Service GmbH Merseburg |
| Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de |
| Unser Weiterbildungsangebot: https://www.psm-merseburg.de/weiterbildung |
| PSM bei Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg |
TABOR-Beziehung
Grundlagen der TABOR-Beziehung
Die Kenntnis des Zusammenhanges zwischen Härte und anderen mechanischen Kenngrößen, z. B. Festigkeit, E-Modul und Zähigkeit, ist sowohl aus prüftechnischer Sicht als auch für das Verständnis des makroskopischen Werkstoffverhaltens von außerordentlich praktischem Interesse. Auf experimenteller Basis gefundene empirische Zusammenhänge ermöglichen eine zeit- und kostensparende Qualitätsüberwachung von Werkstoffen und Bauteilen. Dabei ist jedoch zu beachten, dass diese empirischen Korrelationen nur innerhalb bestimmter Werkstoffklassen gültig sind. Aus der Härteprüfung metallischer Werkstoffe ist eine Abschätzung der Fließspannung bzw. Streckgrenze aus der Härte über die TABOR-Beziehung bekannt. Für ideal plastisches Werkstoffverhalten gilt lineare Proportionalität in der Form:
mit
| pm | senkrecht zur Kontaktfläche Indenter / Prüfkörper wirkender Plastizitätsdruck (pm = 1,08 VH für die Vickerspyramide); | |
| c | Proportionalitätsfaktor |
Härteumwertung
Als Faustformel für die Abschätzung der Zugfestigkeit eines Werkstoffes wird für den Faktor c häufig der Wert ≈ 3 angegeben. Nach einer Zusammenstellung von H. Blumenauer werden im Schrifttum für unterschiedliche metallische Werkstoffe folgende Werte für den Faktor c vorgeschlagen:
c ≈ 3,5 für Stahl (krz-Fe-Matrix)
c ≈ 5,5 für Cu und Cu-Legierungen geglüht
c ≈ 4,0 für Cu und Cu-Legierungen kaltverformt
c ≈ 3,7 für Al und Al-Legierungen.
Der Rückgriff auf solche Faustformeln sollte, wenn er überhaupt erfolgt, nach Möglichkeit von einigen Vor- oder Stichversuchen im konkreten Anwendungsfall begleitet werden. Durch Umwerten (siehe auch Härteumwertung) gewonnene Kenngrößen sind grundsätzlich als solche zu kennzeichnen.
Vickers-Härte/Streckspannung-Korrelation ausgewählter Kunststoffe
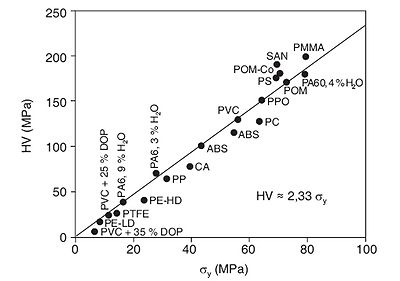
Die TABOR-Gleichung ist die grundlegende Beziehung für die Darstellung des Zusammenhanges zwischen Härte und Streckgrenze. Von WEILER wurde für eine Vielzahl von Thermoplasten der empirische Zusammenhang zwischen getrennt ermittelter Vickers-Härte und Streckspannung bei Zugbeanspruchung ermittelt (Bild 1). Für die im Bild angegebene Werkstoffpalette wird die Beziehung HV ≈ 2,33 σy abgeleitet.
| Bild 1: | Relation zwischen konventioneller Vickershärte (Prüfkraft 2 N) und der Streckspannung aus dem Zugversuch |
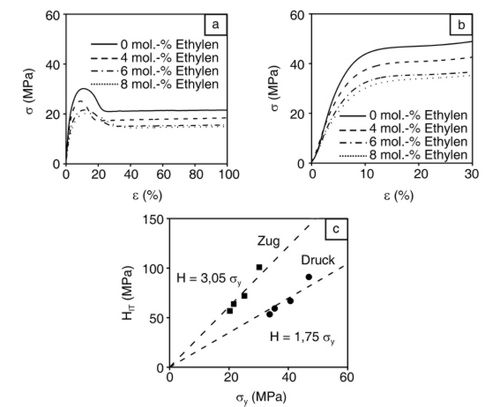
Bei der Betrachtung solcher Zusammenhänge müssen grundsätzlich methodische und werkstoffliche Aspekte berücksichtigt werden. Die Gleichung definiert den Zusammenhang zwischen Druckfließspannung (siehe Druckversuch) und Härte, d. h. Korrelationen zwischen Streckspannungen aus dem Zugversuch und Härtewerten müssen zu Abweichungen von C = 3 führen, da durch das Auftreten einer hydrostatischen Komponente bei Druckbeanspruchung ein unterschiedliches Deformationsverhalten auftritt. Dies wird am Beispiel von Spannungs-Dehnungs- und Druckspannungs-Stauchungs-Kurven von Ethylen/Propylen (Kurzzeichen: E/P)-Copolymeren in Bild 2 dargestellt. Die entsprechenden Streckspannungs- und Druckfließspannungswerte sind in Bild 2c in Korrelation zur Eindringhärte dargestellt. Aus den funktionellen Zusammenhängen werden deutliche Unterschiede zwischen Zugbeanspruchung (HIT = 3,05 σy) und Druckbeanspruchung (HIT = 1,75 σy) ersichtlich, die in der Literatur auch für Polyethylen (Kurzzeichen: PE)-Werkstoffe gefunden werden.
| Bild 2: | Zugspannungs-Dehnungs- (a) und Druckspannungs-Stauchungs-Diagramme (b) für E/P-Copolymere mit unterschiedlichen Ethylengehalten; Korrelation zwischen Eindringhärte HIT und Streckspannung bzw. Druckfließspannung σy (c) |
Abschätzung der Fließspannung
Bei elastisch-plastischem Werkstoffverhalten muss zusätzlich zur Korrelation zwischen Härte und Streckgrenze die Beziehung zum E-Modul Berücksichtigung finden.
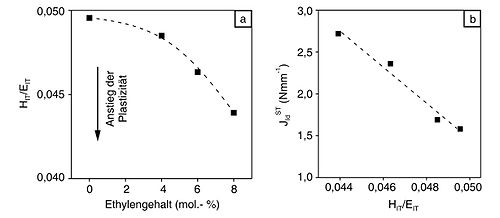
Allgemein gilt, dass kleinere Werte von H/E eine höhere Plastizität bedeuten, die mit höheren Zähigkeitswerten verbunden ist. In Auswertung der in Bild 2 dargestellten Ergebnisse wird in Bild 3a gezeigt, dass der Quotient HIT /EIT von statistischen E/P-Copolymeren mit zunehmendem Ethylengehalt kleiner wird. Für die im instrumentierten Kerbschlagbiegeversuch bei schlagartiger Beanspruchung (siehe: Schlagbeanspruchung Kunststoffe) ermittelten JIdST-Werte wird mit zunehmendem Ethylengehalt eine Erhöhung der Zähigkeit festgestellt. Daraus ergibt sich in Zusammenhang mit Bild 3a je kleiner HIT /EIT, desto größer der Widerstand gegenüber instabiler Rissausbreitung (Bild 3b). Von STUDMAN wurde auf der Basis eines Modells von JOHNSON eine Beziehung vorgeschlagen, die es ermöglicht, mit Hilfe der experimentell ermittelten Härte und des E-Moduls bei Druckbeanspruchung, Fließspannungswerte abzuschätzen.
mit
| β | Kontaktwinkel zwischen Prüfkörper und Indenter (β = 19,7° für die Vickers-Pyramide) |
Dieses Verfahren ist immer dann vorteilhaft anwendbar, wenn aus der Druckspannungs-Stauchungs-Kurve keine Druckfließspannungswerte entnommen werden können oder diese experimentell nicht zugänglich sind. Aus der Gleichung ist ersichtlich, dass die Fließspannung im Wesentlichen durch den Härtekennwert bestimmt ist, der E-Modul wird nur als Korrekturgröße im logarithmischen Term wirksam.
| Bild 3: | Abhängigkeit des Quotienten HIT/EIT vom Ethylengehalt (a) und Zusammenhang zwischen dem Widerstand gegenüber instabiler Rissausbreitung JIdST und dem Quotienten HIT/EIT (b) für E/P-Copolymere |
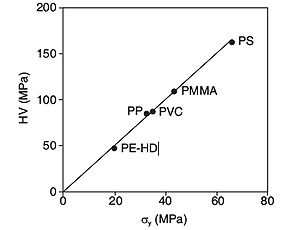
In Bild 4 wird für ausgewählte Thermoplaste der Zusammenhang zwischen Härte unter Last aus der instrumentierten Härteprüfung und Fließspannung dargestellt. Das Verhältnis von Härte und Fließspannung wird unabhängig vom Werkstoff durch die Relation HV/σy = 2,5 beschrieben. Auf Grund des viskoelastisch-plastischen Materialverhaltens, das bei konventionell ermittelten Härtewerten zu größeren Streuungen führen kann, sind zur Berechnung von Fließspannungswerten die physikalisch relevanten Kennwerte der instrumentierten Härteprüfung gegenüber konventionell ermittelten vorzuziehen.
| Bild 4: | Abhängigkeit der Vickers-Härte unter Last HV von der Fließspannung σy |
Literaturhinweise
- Weiler, W. W., Leeb, D., Müller, K., Rupp, D. M.: Härteprüfung an Metallen und Kunststoffen. Expert Verlag, Renningen (1985) (ISBN 3-8169-0013-5; siehe AMK-Büchersammlung unter M 25)
- Baltá-Calleja, F. J., Fakirov, S.: Microhardness of Polymers. Cambridge University Press (2000) (ISBN 978-0-5216-4218-7)
- Koch, T.: Morphologie und Mikrohärte von Polypropylen-Werkstoffen. Dissertation, Technische Universität Wien (2003), Mensch & Buchverlag (2005), (ISBN 3-89820-854-0; siehe AMK-Büchersammlung unter C 30)
- Tabor, D.: The Hardness of Metals. Oxford, Clarendon Press (1951) (ISBN 978-0-1985-0776-5)
- Studman, C. J., Moore, M. A., Jones, S. E.: On the Correlation of Indentation Experiments. J. Phys. D: Appl. Phys. 10 (1977) 949–956
- Johnson, K. L.: The Correlation of Indentation Experiments. J. Mech. Phys. Solids 18 (1970) 115–126
- May, M., Fröhlich, F., Grau, P., Grellmann, W.: Anwendung der Methode der registrierenden Mikrohärteprüfung für die Ermittlung von mechanischen Materialkennwerten an Polymerwerkstoffen. Plaste Kautschuk 30 (1983) 149–153 Download als pdf


![{\displaystyle {\frac {p_{m}}{\sigma _{y}}}\,=\,0{,}5+{\frac {2}{3}}\left[1+\ln \left({\frac {E\tan \beta }{3\sigma _{y}}}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/69df0fe5a974e55919992c572f4038fe3a50e9c9)