Eindringmodul: Unterschied zwischen den Versionen
Die Seite wurde neu angelegt: „{{PSM_Infobox}} <span style="font-size:1.2em;font-weight:bold;">Eindringmodul</span> Der Eindringmodul E<sub>IT</sub> (in MPa) wird im Mikro- und Mikrolastbereic…“ |
Keine Bearbeitungszusammenfassung |
||
| Zeile 32: | Zeile 32: | ||
Die zur Berechnung von E<sub>IT</sub> benötigte [[Querkontraktion]]szahl (Poisson-Zahl) ist für die meisten Werkstoffe bekannt und relativ temperaturunabhängig. Der Wert 8,73 x 10<sup>-13</sup> Pa<sup>-1</sup> ist die effektive Nachgiebigkeit von Diamant. | Die zur Berechnung von E<sub>IT</sub> benötigte [[Querkontraktion]]szahl (Poisson-Zahl) ist für die meisten Werkstoffe bekannt und relativ temperaturunabhängig. Der Wert 8,73 x 10<sup>-13</sup> Pa<sup>-1</sup> ist die effektive Nachgiebigkeit von Diamant. | ||
Bei der Anwendung des Eindringmodul E<sub>IT</sub> ist unbedingt zu beachten, dass E<sub>IT</sub> zwar grundsätzlich die Bedeutung eines [[Elastizitätsmodul]]s hat, dieser jedoch das | Bei der Anwendung des Eindringmodul E<sub>IT</sub> ist unbedingt zu beachten, dass E<sub>IT</sub> zwar grundsätzlich die Bedeutung eines [[Elastizitätsmodul]]s hat, dieser jedoch das [[Steifigkeit]]­sverhalten nur sehr lokal und unter [[Mehrachsiger Spannungszustand|dreiachsiger]] Beanspruchung beschreibt. Hierdurch entsteht ein auch wertmäßiger Unterschied zu den [[Kennwert]]en des [[Elastizitätsmodul]]s, welche mittels konventioneller Verfahren der [[Kunststoffprüfung]], wie dem [[Einachsiger Spannungszustand|einachsigen]] [[Zugversuch|Zug-]] oder [[Druckversuch]] oder dem [[Biegeversuch#Die_Methode_der_Dreipunktbiegepr.C3.BCfung|Drei]]- bzw. [[Biegeversuch#Die_Methode_der_Vierpunktbiegepr.C3.BCfung|Vierpunktbiegeversuch]], ermittelt wurden. Der Eindringmodul kann demnach nicht zu Dimensionierungszwecken herangezogen werden. | ||
Version vom 16. Februar 2018, 14:50 Uhr
| Ein Service der |
|---|

|
| Polymer Service GmbH Merseburg |
| Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de |
| Unser Weiterbildungsangebot: https://www.psm-merseburg.de/weiterbildung |
| PSM bei Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg |
Eindringmodul
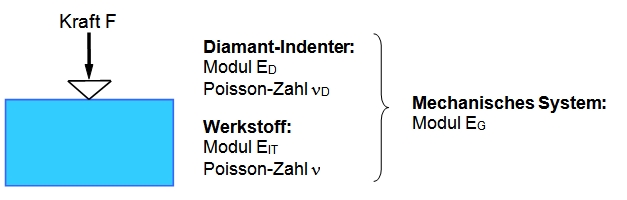
Der Eindringmodul EIT (in MPa) wird im Mikro- und Mikrolastbereich der Härteprüfung mittels eines in DIN EN ISO 14577 ausführlich beschriebenen Verfahrens [1] aus dem Anfangsanstieg der Entlastungskurve des Kraft(F)-Eindringtiefe(h)-Diagramms (siehe Instrumentierte Härteprüfung) bei der Maximalkraft Fmax (dF/dh|Fmax) ermittelt. Im Nanolastbereich der Härteprüfung wird zumeist das Verfahren nach Oliver und Pharr angewandt [2]. Nach DIN EN ISO 14577 wird dabei berücksichtigt, dass eine Parallelschaltung der mechanischen Widerstände von Prüfkörper und Diamant-Eindringkörper vorliegt (siehe Bild und Gleichung 1):
| (1) |
Somit ergibt sich EIT zu:
| (2) |
woraus unter Anwendung von in DIN EN ISO 14577 ausführlich dargestellten Zusammenhänge der folgende Ausdruck abgeleitet werden kann:
| (3) |
Die zur Berechnung von EIT benötigte Querkontraktionszahl (Poisson-Zahl) ist für die meisten Werkstoffe bekannt und relativ temperaturunabhängig. Der Wert 8,73 x 10-13 Pa-1 ist die effektive Nachgiebigkeit von Diamant.
Bei der Anwendung des Eindringmodul EIT ist unbedingt zu beachten, dass EIT zwar grundsätzlich die Bedeutung eines Elastizitätsmoduls hat, dieser jedoch das Steifigkeitsverhalten nur sehr lokal und unter dreiachsiger Beanspruchung beschreibt. Hierdurch entsteht ein auch wertmäßiger Unterschied zu den Kennwerten des Elastizitätsmoduls, welche mittels konventioneller Verfahren der Kunststoffprüfung, wie dem einachsigen Zug- oder Druckversuch oder dem Drei- bzw. Vierpunktbiegeversuch, ermittelt wurden. Der Eindringmodul kann demnach nicht zu Dimensionierungszwecken herangezogen werden.
Literaturhinweise
| [1] | DIN EN ISO 14577: Metallische Werkstoffe – Instrumentierte Eindringprüfung zur Bestimmung der Härte und anderer Werkstoffparameter
|
| [2] | Oliver, W. C., Pharr, G. M.: An Improved Technique for Determining Hardness and Elastic Modulus using Load and Displacement Sensing Indentation. J. of Materials Research 7 (1992) 1564–1583 |