|
|
| Zeile 1: |
Zeile 1: |
| {{PSM_Infobox}} | | {{PSM_Infobox}} |
| <span style="font-size:1.2em;font-weight:bold;">Elastizitätsmodul</span> | | <span style="font-size:1.2em;font-weight:bold;">Elastizität Kunststoffe</span> |
| __FORCETOC__
| |
| ==Einleitung==
| |
| Der Elastizitätsmodul E ist auch bei [[Kunststoffe]]n neben der [[Poissonzahl]] eine wesentliche [[Kenngröße]] zur Beschreibung der energieelastischen Eigenschaften. Die in [[Quasistatische Prüfverfahren|quasistatischen Prüfungen]] wie dem [[Zugversuch|Zug]]-, [[Biegeversuch|Biege]]- oder [[Druckversuch]] ermittelten Kurzzeitmoduli E<sub>t</sub>, E<sub>f</sub> und E<sub>c</sub> sind für die Qualitätssicherung, die Werkstoffentwicklung und -optimierung als auch einfache Dimensionierungsaufgaben (siehe: [[Kunststoffbauteil|Kunststoffbauteil, Dimensionierung]]) geeignet, aber nicht für anspruchsvolle konstruktive Anwendungen nutzbar. In diesem Fall muss z. B. der Kriechmodul aus Langzeitexperimenten auch in Abhängigkeit von der Prüftemperatur verwendet werden.<br>
| |
| Die strukturelle Ursache des [[Energieelastizität|energieelastischen Verhaltens]] von Kunststoffen ist die Veränderung (Dehnung, Stauchung) der mittleren Atomabstände und Bindungswinkel bei Einwirkung mechanischer [[Beanspruchung]]en. Die dabei geleistete mechanische Arbeit wird in Form potentieller Energie gespeichert (Zunahme der inneren Energie) und bei Aufhebung der [[Beanspruchung]] vollständig zurückgewonnen (1. Hauptsatz der Thermodynamik). Infolge seiner strukturellen Ursachen ist das energieelastisches Verhalten auf den Bereich kleiner Verformungen beschränkt. Es besteht eine völlige Reversibilität der [[Deformation]], wobei der Zusammenhang zwischen Beanspruchung und Deformation linear oder nichtlinear sein kann. Die Be- und Entlastungkurve ist in jedem Fall identisch, wodurch keine Hysterese entsteht. Wird ein linearer Zusammenhang zwischen Spannung (Kraft) und Dehnung (siehe auch: [[Deformation]]) beobachtet, dann kann der Zusammenhang im Fall einer [[Einachsiger Spannungszustand|uniaxialen]] Zug- oder Druckbelastung in Analogie zu einer Feder- oder Proportionalitätskonstante durch das [[HOOKE´sche Gesetz]] (Gl. 1) eindeutig beschrieben werden ('''Bild 1''').
| |
|
| |
|
| [[Datei:Elastizitaetsmodul-1.JPG|500px]] | | Die meisten Werkstoffe, oder besser gesagt die Formkörper daraus, zeigen unter bestimmten Voraussetzungen ein elastisches Verhalten, das heißt bei Belastung dehnen sie sich aus, bei Entlastung geht die Dehnung wieder zurück. |
| | |
| | [[Datei:elastizitaet_l.jpg]] |
| {| | | {| |
| |- valign="top" | | |- valign="top" |
| |width="50px"|'''Bild 1''': | | |width="50px"|'''Bild 1''': |
| |width="600px"|Elastische Deformation des Federmodells und des Festkörpers nach HOOKE | | |width="600px" |Deformationsverhalten von Kunstoffen: a) elastisch, b) linear-viskoelastisch und c) nichtlinear-viskoelastisch |
| |}
| |
| | |
| Die [[Energieelastizität]] dominiert das Verhalten von [[Polymer]]werkstoffen insbesondere bei kleinen Verformungen und bei tiefen Temperaturen sowie bei hohen [[Verformungsgeschwindigkeit]]en (siehe auch: [[Dehnrate Grundlagen]]), wobei die klassische Energieelastizitätstheorie hier wesentlich zum Verständnis des [[Deformation]]sverhaltens der Kunststoffe beiträgt. Darüber hinaus liefert sie in diesem Bereich brauchbare Näherungslösungen für die quantitative Beschreibung des Spannungs-Dehnungs-Zusammenhanges (siehe auch: [[Zugversuch#Zugversuch.2C_Spannung-Dehnung-Diagramm|wahres Spannungs-Dehnungs-Diagramm]]) zumindest bei uniaxialer Normalbeanspruchung [1].<br>
| |
| In der prüftechnischen Praxis werden im Wesentlichen drei Methoden zur Ermittlung des Elastizitätsmoduls angewandt. Dies sind die [[Quasistatische Prüfverfahren|quasistatischen]] Versuche der [[Kunststoffprüfung]], die dynamisch-mechanische Analyse und die [[Ultraschallprüfung]], wobei die mechanischen Kurzzeitversuche (siehe: [[Zugversuch]]) die höchste Praxisrelevanz besitzen.
| |
| | |
| ==Prüfmethoden zur Ermittlung des Elastizitätsmoduls==
| |
| ===Quasistatische Kurzzeitversuche===
| |
| | |
| Zur Ermittlung des Elastizitätsmoduls E werden in der quasistatischen Kunststoffprüfung der [[Zugversuch|Zug]]-, [[Biegeversuch|Biege]]- und [[Druckversuch]] unter Nutzung einer [[Materialprüfmaschine|Universalprüfmaschine]] angewandt. Im Gegensatz zur Prüfung metallischer Werkstoffe (siehe auch: [[Werkstoffprüfung]]), wo der E-Modul als Tangentenmodul im Ursprung des Spannungs-Dehnungs-Diagramm ermittelt wird, wird bei normenkonformer [[Kunststoffprüfung|Prüfung von Kunststoffen]] der Sekantenmodul bestimmt. Die Begründung liegt in dem vergleichsweise geringen elastischen [[Deformation]]sbereich von < 0,1 % Dehnung und in dem [[linear-viskoelastisches Verhalten|linear-viskoelastischen Verhalten]], welches bis etwa 0,3 % registriert wird. Dem, wenn auch zeitabhängigen, reversiblen Dehnungsbereich bis 0,3 % folgt dann der Bereich der nichtlinearen Viskoelastizität, indem erste irreversible [[Mikroschädigungsgrenze|Mikroschädigungen]] und -deformationen auftreten. Aus diesem Grund wurden die Dehngrenzen in den drei angegebenen Prüfmethoden [2–4] mit 0,05 und 0,25 % angegeben und die korrespondierenden Spannungswerte werden im Versuch ermittelt ('''Bild 2'''). Zur Vermeidung von Anlaufeffekten im z. B. [[Zugversuch]] wird ein Offset von 0,05 % eingestellt oder eine Vorkraft angegeben, die diesen Dehnungswert hervorruft. Der Versuch, der mit einer [[Dehnrate Grundlagen|Dehnrate]] von näherungsweise 1 %/min durchgeführt wird, wird oberhalb 0,3 % abgebrochen oder wird mit der [[Prüfgeschwindigkeit]] von z. B. 50 mm/min als Zugversuch bis zum Versagen des Prüfkörpers fortgeführt [6]. Die Elastizitätsmoduli E<sub>t</sub>, E<sub>f</sub> oder E<sub>c</sub> werden einheitlich nach der Gl. (1) berechnet, wobei die Dehnung im [[Zugversuch]] ε, die [[Randfaserdehnung]] im [[Biegeversuch]] ε<sub>f</sub> oder die Stauchung im [[Druckversuch]] ε<sub>c</sub> als Vorgabewerte benutzt werden.
| |
| | |
| [[Datei:Elastizitaetsmodul-2.JPG|500px]]
| |
| {|
| |
| |- valign="top"
| |
| |width="50px"|'''Bild 2''':
| |
| |width="600px"|Ermittlung des Tangentenmoduls an Metallen (a) und des Sekantenmoduls bei Kunststoffen (b)
| |
| |}
| |
| | |
| {|
| |
| |-
| |
| |width="20px"|
| |
| |width="500px"|<math>E=\frac{\sigma_{2}-\sigma_{1}}{\epsilon_{2}-\epsilon_{1}}=\frac{\sigma_{2}-\sigma_{1}}{0,0025 - 0,0005}=\frac{\Delta\sigma}{0,002}</math>
| |
| |(1)
| |
| |}
| |
| | |
| Bei Bedarf können diese Versuche auch in einer Temperierkammer durchgeführt werden, wodurch der E-Modul als Funktion der Temperatur darstellbar ist.
| |
| | |
| ===Dynamisch-Mechanische Analyse (DMA)===
| |
| | |
| Bei der dynamisch-mechanischen Analyse oder Spektroskopie wird der Prüfkörper einer periodisch wechselnden, zumeist sinusförmigen Beanspruchung, ausgesetzt. Der Vorteil dieser Methode ist bei Verwendung einer Temperierkammer (dynamisch-mechanisch thermische Analyse – DMTA), dass die dynamisch-mechanischen Kennwerte als Funktion der Temperatur vorliegen ('''Bild 3'''). Durch die Variation der Frequenz ist zusätzlich die Charakterisierung der Zeitabhängigkeit des Werkstoffverhaltens möglich. Die dynamisch-mechanische Analyse kann dabei mit freien gedämpften Schwingungen (Pendelschwingungen) oder im erzwungenen Schwingungs- sowie Resonanzmodus durchgeführt werden. Üblicherweise werden dabei die [[Beanspruchung]]sarten Torsion, Biegung und Zug genutzt. Gemeinsam ist allen Verfahren, dass die [[Deformation]] des [[Prüfkörper]]s sehr klein ist und den [[linear-viskoelastisches Verhalten|linear-viskoelastischen]] Bereich nicht überschreiten sollte. Infolge dieser kleinen Verformungen sind mit der DMA oder DMTA im Temperaturintervall von ca. –180 °C bis 400 °C hohe Prüffrequenzen bei mechanischer Anregung bis 200 Hz realisierbar [1, 7].
| |
| | |
| [[Datei:Elastizitaetsmodul-3.JPG|300px]]
| |
| {|
| |
| |- valign="top"
| |
| |width="50px"|'''Bild 3''':
| |
| |width="600px"|DMTA-System Eplexor der Fa. NETSCH Instruments GmbH, Ahlen
| |
| |}
| |
| | |
| Für die [[Kunststoffprüfung]] mittels [[Dynamisch-Mechanische Analyse (DMA) – Zugbeanspruchung|DMA oder DMTA unter Zugbeanspruchung]] [8] werden zur Erzeugung sinusförmiger Dehnungen oder Spannungen vorwiegend hydraulische, pneumatische oder elektrodynamische Kleinprüfmaschinen sowie DMTA-Systeme mit Zusatzeinrichtungen wie Dehnungssensoren und Temperierkammern ('''Bild 3''') verwendet. Von dem Prüfsystem wird dann eine konstante sinusförmige Dehnungs- oder Spannungsamplitude mit einer definierten und konstanten Frequenz auf den Prüfkörper aufgebracht, wobei in der Kunststoffprüfung aufgrund der [[Prüfkörper]]geometrie bevorzugt im Zugschwellbereich gearbeitet wird. Die Amplitude der Spannung oder Dehnung sowie die Mittelspannung oder -dehnung als auch die Temperatur werden per PID-Regelung auf konstantem Niveau gehalten, um [[Kriechen Kunststoffe|Kriech]]- oder [[Relaxation Kunststoffe|Relaxationseffekte]] während des Versuchs zu kompensieren. Bei [[linear-viskoelastisches Verhalten|linear-viskoelastischem Werkstoffverhalten]] und einem Normalspannungszustand weisen die zeitlichen Änderungen von Spannung und [[Deformation]] im eingeschwungenen Zustand die gleiche Frequenz aber unterschiedliche Phasenlagen (Gln. 2 und 3) auf ('''Bild 4'''), wobei δ der Phasenwinkel ist, der Werte zwischen 0 und π/2 annehmen kann.
| |
| | |
| {|
| |
| |-
| |
| |width="20px"|
| |
| |width="500px"|<math>\epsilon(t)=\epsilon_{0}\cdot \sin (\omega t)</math>
| |
| |(2)
| |
| |}
| |
| | |
| {|
| |
| |-
| |
| |width="20px"|
| |
| |width="500px"|<math>\sigma(t)=\sigma_{0}\cdot \sin (\omega t - \delta)</math>
| |
| |(3)
| |
| |}
| |
| | |
| Für den Zusammenhang zwischen der Beanspruchungszeit t und Frequenz f bzw. Kreisfrequenz ω gilt Gl. (4):
| |
| | |
| {|
| |
| |-
| |
| |width="20px"|
| |
| |width="500px"|<math>t=\frac{1}{2\pi f}=\frac{1}{\omega}</math>
| |
| |(4)
| |
| |}
| |
| | |
| [[Datei:Elastizitaetsmodul-4.JPG|500px]]
| |
| {|
| |
| |- valign="top"
| |
| |width="50px"|'''Bild 4''':
| |
| |width="600px"|Schematischer Aufbau des Prüfsystems und zeitliche Änderung von Spannung und Dehnung bei der DMA mittels erzwungener Schwingungen
| |
| |}
| |
| | |
| Aufgrund der Phasenverschiebung δ zwischen Spannung σ und Dehnung ε wird zur Beschreibung des Spannungs-Dehnungs-Zusammenhanges der E-Modul als komplexe Kenngröße E* eingeführt. Der komplexe Modul kann dabei als Vektor in der komplexen Zahlenebene betrachtet werden ('''Bild 5'''), dessen Richtung durch den Phasenwinkel δ und dessen Betrag durch das Verhältnis der Amplitudenwerte von Spannung und Dehnung bestimmt ist (Gl. 5):
| |
| | |
| {|
| |
| |-
| |
| |width="20px"|
| |
| |width="500px"|<math>\left | E^{*} \right |=\frac{\sigma_{0}}{\epsilon_{0}}</math>
| |
| |(5)
| |
| |}
| |
| | |
| [[Datei:Elastizitaetsmodul-5.JPG|300px]]
| |
| {|
| |
| |- valign="top"
| |
| |width="50px"|'''Bild 5''':
| |
| |width="600px"|Darstellung des komplexen Zug-E-Modul aus der DMTA
| |
| |}
| |
| | |
| Unter Nutzung einfacher trigonometrischer Beziehungen kann eine Aufspaltung in einen Realteil E‘ (Speichermodul) und den Imaginärteil E‘‘ (Verlustmodul) nach den Gln. (6) und (7) vorgenommen werden, wobei ingenieurtechnisch der Speichermodul von speziellem Interesse ist.
| |
| | |
| {|
| |
| |-
| |
| |width="20px"|
| |
| |width="500px"|<math>E^{\prime}=E\text{*}\cdot\cos\delta=\frac{\sigma_{0}}{\epsilon_{0}}\cdot\cos\delta </math>
| |
| |(6)
| |
| |} | | |} |
|
| |
|
| {|
| | Handelt es sich um eine momentan reversible Verformung, so spricht man von idealer Elastizität. Sind Spannung und Dehnung proportional, so liegt eine HOOKE´sche Elastizität (siehe [[HOOKE´sche Gesetz]]) vor, der Sonderfall des ideal elastischen Verhaltens. |
| |-
| |
| |width="20px"|
| |
| |width="500px"|<math>E^{\prime\prime}=E\text{*}\cdot\sin\delta=\frac{\sigma_{0}}{\epsilon_{0}}\cdot\sin\delta </math>
| |
| |(7)
| |
| |}
| |
| | |
| Aus dem Verhältnis von Verlust- und Speichermodul ergibt sich der Verlustfaktor tan δ, der das Dämpfungsverhalten des Werkstoffs charakterisiert (Gl. 8).
| |
| | |
| {|
| |
| |-
| |
| |width="20px"|
| |
| |width="500px"|<math>\tan\delta=\frac{E^{\prime\prime}}{E^{\prime}} </math>
| |
| |(8)
| |
| |}
| |
|
| |
|
| Im Regelfall ist der dynamische Speichermodul aufgrund der [[Beanspruchung|schwingenden Beanspruchung]] etwas höher als der E-Modul aus den [[Quasistatische Prüfverfahren|quasistatischen Versuchen]]. Das Verfahren der erzwungenen Schwingungen ist auf Frequenzen unterhalb der Resonanzfrequenz des Prüfkörpers beschränkt. Die Regelung der Messung kann sowohl dehnungs- als auch spannungsgeregelt (siehe: [[Zugversuch Regelung]]) erfolgen, was die Bestimmung des komplexen Moduls E* und der komplexen [[Probennachgiebigkeit|Prüfkörpernachgiebigkeit]] C* ermöglicht.<br>
| | Die ideale Elastizität beruht auf einer reversiblen Änderung der Lagen von Atomen und Atomgruppen. Dieses elastische Verhalten ist charakteristisch für Keramik und viele Metalle sowie für [[Thermoplaste|thermoplastische Kunststoffe]] unterhalb der [[Glastemperatur|Glasübergangstemperatur]] bei geringer Dehnung. |
| Auf Grund ihrer großen Anwendungsbreite (Torsion, Zug, Biegung und Scherung) haben Verfahren mit erzwungenen Schwingungen heute eine dominierende Rolle bei der [[Dynamisch-Mechanische Analyse (DMA) – Grundlagen|dynamisch-mechanischen Analyse]] polymerer Werkstoffe.<br>
| |
| Eine näherungsweise Ermittlung des E-Moduls ist auch bei Verwendung des Torsionsschwingversuchs aus dem [[Schubmodul|Schubmodul G]] möglich, falls die [[Poissonzahl]] µ im entsprechenden Temperaturintervall bekannt ist (Gl. 9).
| |
|
| |
|
| {|
| | Der Zyklus von Belastung und Entlastung bei HOOKE'scher elastischer Verformung erfolgt ohne Austausch von Arbeit und Wärme (∑A = O und ∑Q = O) sowie reversibel. Theoretisch sind diese bildlich dargestellten Zyklen ('''Bild 1a''') deshalb unendlich wiederholbar, ohne dass eine Änderung des [[Elastizitätsmodul]]s auftritt. |
| |-
| |
| |width="20px"|
| |
| |width="500px"|<math>E^{\prime}=2G^{\prime}\cdot(1+\mu)</math>
| |
| |(9)
| |
| |}
| |
|
| |
|
| ===[[Ultraschallprüfung]]===
| | [[Kunststoffe]] verhalten sich im Allgemeinen jedoch viskoelastisch. Die [[viskoelastisches Werkstoffverhalten|Viskoelastizität]] ist eine verzögerte Elastizität. Sie beruht auf Relaxationsvorgängen (siehe: [[Relaxation Kunststoffe]]), d. h. auf Rückstellvorgängen der Molekülketten, die mehr oder weniger Zeit beanspruchen. |
|
| |
|
| Im Bereich hoher Frequenzen kann der dynamische E-Modul auch mit einem dielektrischen Messplatz ermittelt werden oder es wird die Ausbreitung von Schall- und Ultraschallwellen zur Kennwertermittlung verwendet [9, 10].<br>
| | [[Viskoelastisches Werkstoffverhalten|Viskoelastische Vorgänge]] sind hinsichtlich der Verformung, jedoch nicht hinsichtlich des Verformungsweges meist vollständig reversibel ('''Bild 1b'''). Je nach [[Kunststoffe|Kunststoff]] und Belastung kann das vollständige Erreichen der Ausgangslänge nach Entlastung jedoch durch irreversible Vorgänge partiell behindert sein. Der Zyklus von viskoelastischer Belastung und Entlastung erfolgt unter irreversibler Umwandlung von Arbeit (∑A > 0) in Wärme (∑Q < 0) ('''Bild 1c'''). |
| Oberhalb der Resonanzfrequenz wird die Wellenlänge λ der schwingenden mechanischen [[Beanspruchung]] klein im Vergleich zu den Prüfkörperabmessungen. Dadurch ist es möglich, die Charakteristik der Wellenausbreitung im Werkstoff zur Bestimmung der [[viskoelastisches Werkstoffverhalten|viskoelastischen Eigenschaften]] zu nutzen. Die Messungen werden üblicherweise mittels Ultraschall (f > 20 kHz) im [[Ultraschall-Impuls-Echo-Technik|Impuls-Echo-]] oder [[Ultraschall-Durchschallungs-Technik|Durchschallungsverfahren]] durchgeführt [1]. Dabei werden die [[Schallgeschwindigkeit]]en c (Gl. 10) und der Schallabsorptionskoeffizient α (Gl. 11) aus der akustischen Weglänge d und der zugehörigen Impulslaufzeit t sowie den Amplituden A<sub>1</sub> und A<sub>2</sub> bei unterschiedlichen Weglängen d<sub>1</sub> und d<sub>2</sub> ermittelt.
| |
|
| |
|
| {|
| | Gummielastisches Verhalten zeigen weitmaschig vernetzte [[Polymer]]e, so genannte [[Elastomere]], oberhalb der [[Glastemperatur|Glasübergangstemperatur]], [[Thermoplaste|thermoplastische Kunststoffe]] im quasi-gummielastischen Bereich und teilweise auch die Schmelzen von thermoplastischen Kunststoffen. Die [[Gummielastizität]] beruht auf dem Bestreben der Kettenmoleküle, die statistisch wahrscheinlichste verknäuelte Form anzunehmen, die dem entropisch günstigstem Zustand entspricht (siehe auch: [[Entropieelastizität]]). |
| |- | |
| |width="20px"|
| |
| |width="500px"|<math>c=\frac{d}{t}</math>
| |
| |(10)
| |
| |}
| |
|
| |
|
| {|
| |
| |-
| |
| |width="20px"|
| |
| |width="500px"|<math>\alpha=\frac{1}{d_{2}-d_{1}}\quad In\quad \frac{A_{1}}{A_{2}}</math>
| |
| |(11)
| |
| |}
| |
|
| |
|
| Unter Verwendung von Longitudinalwellen (c<sub>L</sub>, α<sub>L</sub>) und Transversalwellen (c<sub>T</sub>, α<sub>T</sub>) können bei Kenntnis der [[Dichte]] ρ des Werkstoffs der Longitudinalwellenmodul L und der [[Schubmodul|Schermodul]] G bestimmt werden. Bei geringer Dämpfung (αλ/2π << 1) gelten dann näherungsweise die Gln. (12) und (13).
| | '''Literaturhinweis''' |
|
| |
|
| {|
| | * Fonds der Chemischen Industrie: Folienserie "Neue Werkstoffe". Oehms Druck GmbH, Frankfurt/Main (1992) Folie 27 (ISBN 0174-366X) |
| |-
| |
| |width="20px"|
| |
| |width="500px"|<math>L^{\prime}= \rho\cdot c_{L}^{2} \quad und\quad L^{\prime\prime}=\frac{2\rho\cdot\alpha_{L}\cdot c_{L}^{3}}{\omega}</math>
| |
| |(12)
| |
| |}
| |
| | |
| {|
| |
| |-
| |
| |width="20px"|
| |
| |width="500px"|<math>G^{\prime}= \rho\cdot c_{T}^{2}\quad und \quad G^{\prime\prime}=\frac{2\rho\cdot\alpha_{T}\cdot c_{T}^{3}}{\omega}</math>
| |
| |(13)
| |
| |}
| |
| | |
| Aus dem Longitudinalwellen- und Schermodul kann entsprechend der Elastizitätstheorie der Elastizitätsmodul E‘ (Gl. 14) berechnet werden, der vom Verhältnis der Ausbreitungsgeschwindigkeiten von Transversal- und Longitudinalwellen abhängig ist.
| |
| | |
| | |
| {|
| |
| |-
| |
| |width="20px"|
| |
| |width="500px"|<math>E^{\prime}=\frac{(3L^{\prime}-4G^{\prime})\cdot(G^{\prime}-1)}{L^{\prime}}=4\rho\cdot c_{T}^{2}\left ( \frac{0,75-\left ( \frac{c_{T}}{c_{L}} \right )^{2}}{1-\left ( \frac{c_{T}}{c_{L}} \right )^{2}} \right )</math>
| |
| |(14)
| |
| |}
| |
| | |
| Ultraschallmessungen finden üblicherweise bei Frequenzen zwischen 100 kHz und 100 MHz statt. Das obere Ende des Frequenzbereiches ist dabei durch die starke Zunahme der Dämpfung gegeben. Für die Arbeit in diesem weiten Frequenzbereich ist die Verwendung unterschiedlicher Schwingungssensoren erforderlich. Relativ große Frequenzbereiche können nach einer breitbandigen Anregung mit Hilfe der [[Frequenzanalyse|Fourier- oder Wavelet-Analyse]] erfasst werden.
| |
| | |
| Eine relativ einfache Methode zur Bestimmung des Elastizitätsmoduls mit Ultraschall ist bei Verwendung von plattenförmigen Prüfkörpern bekannter Dicke d und Dichte ρ gegeben ('''Bild 6''').
| |
| | |
| [[Datei:Elastizitaetsmodul-6.JPG|500px]]
| |
| {|
| |
| |- valign="top"
| |
| |width="50px"|'''Bild 6''':
| |
| |width="600px"|Schematische Darstellung der Durchschallungstechnik mit [[Ultraschall-Normal-Prüfköpfe|Normal-Prüfköpfen]] (a) und [[Ultraschall-Winkel-Prüfköpfe|Winkel-Prüfköpfen]] (b) sowie die [[Ultraschall-Impuls-Echo-Technik|Impuls-Echo-Technik]] (c)
| |
| |}
| |
| | |
| Bei Verwendung von [[Ultraschall-Normal-Prüfköpfe|Normal-Prüfköpfen]] ('''Bild 6a und c''') werden Longitudinalwellen zur Messung genutzt, wobei zu beachten ist, dass bei der [[Ultraschall-Impuls-Echo-Technik|Impuls-Echo-Technik]] die Laufzeit des Ultraschalls doppelt so groß ist wie bei der [[Ultraschall-Durchschallungs-Technik|Durchschallungsmethode]]. Aus dem [[A-Bild-Technik|A-Bild]] kann dann die Laufzeit Δt in Direktankopplung oder [[Ultraschall-Tauchbad-Technik|Tauchbadtechnik]] bei bekannter Dicke und Einschallwinkel γ nach Gl. (15) (Durchschallung) oder (16) (Impuls-Echo-Technik) gemessen und die Longitudinalwellengeschwindigkeit c<sub>L</sub> berechnet werden. Die Traversalwellengeschwindigkeit c<sub>T</sub> wird mit [[Ultraschall-Winkel-Prüfköpfe|Winkel-Prüfköpfen]] nach Gl. (17) ermittelt.
| |
| | |
| {|
| |
| |-
| |
| |width="20px"|
| |
| |width="500px"|<math>c_{L}=\frac{d}{\Delta t}</math>
| |
| |(15)
| |
| |}
| |
| | |
| {|
| |
| |-
| |
| |width="20px"|
| |
| |width="500px"|<math>c_{L}=\frac{2d}{\Delta t}</math>
| |
| |(16)
| |
| |}
| |
| | |
| {|
| |
| |-
| |
| |width="20px"|
| |
| |width="500px"|<math>c_{L}=\frac{2d}{\Delta t \cdot \cos \gamma}</math>
| |
| |(17)
| |
| |}
| |
| | |
| Unter Voraussetzung, dass die [[Poissonzahl]] µ für die Prüftemperatur T bekannt ist, kann dann nach Gl. (18) der Elastizitätsmodul E und nach Gl. (19) der Schubmodul G berechnet werden, wobei zu beachten ist, dass diese Kennwerte frequenzabhängig sind.
| |
| | |
| {|
| |
| |-
| |
| |width="20px"|
| |
| |width="500px"|<math>E=c_{L}^{2}\cdot\rho\frac{(1+\mu)\cdot(1-2\mu)}{(1-\mu)}</math>
| |
| |(18)
| |
| |}
| |
| | |
| {|
| |
| |-
| |
| |width="20px"|
| |
| |width="500px"|<math>G=c_{T}^{2}\cdot\rho</math>
| |
| |(19)
| |
| |}
| |
| | |
| | |
| '''Literaturhinweise'''
| |
| {|
| |
| |-valign="top"
| |
| |[1]
| |
| |Lüpke, T.: Grundlagen mechanischen Verhaltens. In: [[Grellmann,_Wolfgang|Grellmann, W.]], [[Seidler,_Sabine|Seidler, S.]] (Hrsg.): Kunststoffprüfung. Carl Hanser Verlag, München (2015) 3. Auflage S. 91/92, (ISBN 978-3-446-44350-1; siehe [[AMK-Büchersammlung]] unter A 18)
| |
| |-valign="top"
| |
| |[2]
| |
| |DIN EN ISO 527-1 (2019-12): Kunststoffe – Bestimmung der Zugeigenschaften – Teil 1: Allgemeine Grundsätze
| |
| |-valign="top"
| |
| |[3]
| |
| |DIN EN ISO 527-2 (2012-06): Kunststoffe – Bestimmung der Zugeigenschaften – Teil 2: Prüfbedingen für Form- und Extrusionsmassen
| |
| |-valign="top"
| |
| |[4]
| |
| |DIN EN ISO 178 (2019-08): Kunststoffe – Bestimmung der Biegeeigenschaften
| |
| |-valign="top"
| |
| |[5]
| |
| |DIN EN ISO 604 (2003-12): Kunststoffe – Bestimmung von Druckeigenschaften
| |
| |-valign="top"
| |
| |[6]
| |
| |[[Bierögel,_Christian|Bierögel, C.]]: Biegeversuch an Kunststoffen. In: Grellmann, W., Seidler, S. (Hrsg.): Kunststoffprüfung. Carl Hanser Verlag, München (2015) 3. Auflage, S. 147–158 (ISBN 978-3-446-44350-1; siehe [[AMK-Büchersammlung]] unter A 18)
| |
| |-valign="top"
| |
| |[7]
| |
| |DIN EN ISO 6721-1 (2019-09): Kunststoffe – Bestimmung dynamisch-mechanischer Eigenschaften – Teil 1: Allgemeine Grundlagen
| |
| |-valign="top"
| |
| |[8]
| |
| |ISO 6721-4 (2019-05): Kunststoffe – Bestimmung dynamisch-mechanischer Eigenschaften – Teil 4: Zugschwingung – Erzwungene Schwingungen
| |
| |-valign="top"
| |
| |[9]
| |
| |ISO 6721-8 (2019-04): Kunststoffe – Bestimmung dynamisch-mechanischer Eigenschaften – Teil 8: Längs- und Scherschwingung – Wellenausbreitungs-Verfahren
| |
| |-valign="top"
| |
| |[10]
| |
| |ISO 6721-9 (2019-04): Kunststoffe – Bestimmung dynamisch-mechanischer Eigenschaften – Teil 9: Zugschwingung – Schallausbreitungsverfahren
| |
| |-valign="top"
| |
| |[11]
| |
| |Matthies, K. u. a.: Dickenmessung mit Ultraschall. DVS-Verlag GmbH, Berlin, 2. Auflage (1998) (ISBN 3-87155-940-7; siehe [[AMK-Büchersammlung]] unter M 44)
| |
| |}
| |
|
| |
|
| [[Kategorie:Deformation]] | | [[Kategorie:Deformation]] |
| [[Kategorie:Zugversuch]]
| |
Elastizität Kunststoffe
Die meisten Werkstoffe, oder besser gesagt die Formkörper daraus, zeigen unter bestimmten Voraussetzungen ein elastisches Verhalten, das heißt bei Belastung dehnen sie sich aus, bei Entlastung geht die Dehnung wieder zurück.
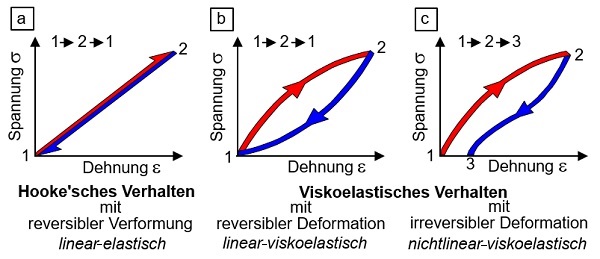
| Bild 1:
|
Deformationsverhalten von Kunstoffen: a) elastisch, b) linear-viskoelastisch und c) nichtlinear-viskoelastisch
|
Handelt es sich um eine momentan reversible Verformung, so spricht man von idealer Elastizität. Sind Spannung und Dehnung proportional, so liegt eine HOOKE´sche Elastizität (siehe HOOKE´sche Gesetz) vor, der Sonderfall des ideal elastischen Verhaltens.
Die ideale Elastizität beruht auf einer reversiblen Änderung der Lagen von Atomen und Atomgruppen. Dieses elastische Verhalten ist charakteristisch für Keramik und viele Metalle sowie für thermoplastische Kunststoffe unterhalb der Glasübergangstemperatur bei geringer Dehnung.
Der Zyklus von Belastung und Entlastung bei HOOKE'scher elastischer Verformung erfolgt ohne Austausch von Arbeit und Wärme (∑A = O und ∑Q = O) sowie reversibel. Theoretisch sind diese bildlich dargestellten Zyklen (Bild 1a) deshalb unendlich wiederholbar, ohne dass eine Änderung des Elastizitätsmoduls auftritt.
Kunststoffe verhalten sich im Allgemeinen jedoch viskoelastisch. Die Viskoelastizität ist eine verzögerte Elastizität. Sie beruht auf Relaxationsvorgängen (siehe: Relaxation Kunststoffe), d. h. auf Rückstellvorgängen der Molekülketten, die mehr oder weniger Zeit beanspruchen.
Viskoelastische Vorgänge sind hinsichtlich der Verformung, jedoch nicht hinsichtlich des Verformungsweges meist vollständig reversibel (Bild 1b). Je nach Kunststoff und Belastung kann das vollständige Erreichen der Ausgangslänge nach Entlastung jedoch durch irreversible Vorgänge partiell behindert sein. Der Zyklus von viskoelastischer Belastung und Entlastung erfolgt unter irreversibler Umwandlung von Arbeit (∑A > 0) in Wärme (∑Q < 0) (Bild 1c).
Gummielastisches Verhalten zeigen weitmaschig vernetzte Polymere, so genannte Elastomere, oberhalb der Glasübergangstemperatur, thermoplastische Kunststoffe im quasi-gummielastischen Bereich und teilweise auch die Schmelzen von thermoplastischen Kunststoffen. Die Gummielastizität beruht auf dem Bestreben der Kettenmoleküle, die statistisch wahrscheinlichste verknäuelte Form anzunehmen, die dem entropisch günstigstem Zustand entspricht (siehe auch: Entropieelastizität).
Literaturhinweis
- Fonds der Chemischen Industrie: Folienserie "Neue Werkstoffe". Oehms Druck GmbH, Frankfurt/Main (1992) Folie 27 (ISBN 0174-366X)


