Ermüdungsrissausbreitung Elastomere: Unterschied zwischen den Versionen
Posch (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 80: | Zeile 80: | ||
|-valign="top" | |-valign="top" | ||
|[9] | |[9] | ||
|[ | |[https://www.coesfeld.com/produkte/d/elastomerpruefung/dynamisch.html https://www.coesfeld.com/produkte/d/elastomerpruefung/dynamisch.html]; (Zugriff am 22.01.2023) | ||
|-valign="top" | |-valign="top" | ||
|[10] | |[10] | ||
| Zeile 89: | Zeile 89: | ||
|-valign="top" | |-valign="top" | ||
|[12] | |[12] | ||
|Eisele, U.: Introduction to Polymer Physics. Springer, Berlin Heidelberg (1990) | |Eisele, U.: Introduction to Polymer Physics. Springer, Berlin Heidelberg (1990) (ISBN 978-3-642-74436-5) | ||
|-valign="top" | |-valign="top" | ||
|[13] | |[13] | ||
Version vom 23. März 2023, 11:48 Uhr
| Ein Service der |
|---|

|
| Polymer Service GmbH Merseburg |
| Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de |
| Unser Weiterbildungsangebot: https://www.psm-merseburg.de/weiterbildung |
| PSM bei Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg |
Ermüdungsrissausbreitung Elastomere
Mess- und Prüftechnische Voraussetzungen
Die Entwicklung und der Einsatz zyklischer (dynamischer) Untersuchungsmethoden von Elastomeren ist eng mit der Entwicklung des „Tear and Fatigue Analyser (TFA) durch die Fa. Bayer in Zusammenarbeit mit der Fa. Coesfeld im Jahr 1992 verbunden [1, 2].
Die Durchführung bruchmechanischer Untersuchungen unter zyklischer Belastung setzt das Vorhandensein der entsprechenden Prüftechnik und auch spezieller Erfahrungen voraus, da die experimentellen Parameter Prüfkörperform und -größe, Vorspannung, Mittelspannung sowie Beanspruchungsfrequenz und -amplitude in weiten Bereichen variiert werden kann. Der Einfluss der Prüfparameter auf die ermittelten Risswachstumskurven wurde z. B. in den Arbeiten [3‒8] dargestellt.
Mit dem Einsatz eines servohydraulischen TFA-Messsystems ist es möglich, praxisnahe Beanspruchungen aufzubringen, z. B. kann die Reifenbeanspruchung, die durch Pulse gekennzeichnet ist, gut simuliert werden. Aus diesem Grund setzt sich die zyklische Prüfung mit TFA-Gerätesystemen immer weiter durch, was auch aus der zunehmenden Anzahl an TFA-Geräten im deutschsprachigen Raum abgeleitet werden kann. Der TFA erlaubt die gleichzeitige Prüfung von bis zu 10 Einzelprüfkörpern, wobei für jeden Prüfkörper separat jeder Be- und Entlastungszyklus aufgezeichnet wird und über den gesamten Zeitraum der Prüfung eine automatische Risslängenerfassung über die Ermittlung der Risskonturlänge mittels einer CCD-Kamera (Bild 1) [9] realisiert wird.
| Bild 1: | TFA-System der Fa. Coesfeld |
Prüfregime
Die Prüfkörper können periodisch zwischen einer maximalen und einer minimalen Spannung (spannungsgeregelt) oder Dehnung (dehnungsgeregelt) belastet werden (siehe Zugversuch Regelung). Während des Experimentes werden verschiedene Daten wie Temperatur, Ozonkonzentration, Zeit, Zyklenzahl und Regelstrecken registriert, wobei die Speicherintervalle frei wählbar sind. Für jeden einzelnen Messplatz werden die Kraft F, die elastische und dissipierte Energiedichte W0 und Wdiss, die Verformung l, die Risskonturlänge aeff und die Regelstrecke der Verstelleinheit separat erfasst. Somit besteht mit einer TFA-Untersuchung eine relativ ökonomische Möglichkeit, Messdaten zur Erzeugung von Risswachstumskurven zu generieren. Zusätzlich kann die Temperatur in der Prüfkammer zwischen –50 °C und 150 °C und optional auch das Klima in der Prüfkammer variiert werden. Es ist beispielsweise eine Prüfung unter Ozoneinfluss möglich, was insbesondere für Elastomere mit ungesättigten Doppelbindungen in der Kette wie z. B. NR, NBR oder SBR von höchster praktischer Relevanz ist. Ursprünglich wurde der TFA für die Untersuchung von SENT-Prüfkörpern ausgelegt, in der jüngeren Vergangenheit haben aber Arbeiten [5, 8] gezeigt, dass der Einsatz von Pure Shear-Prüfkörpern zu bevorzugen ist.
Risswachstumskurve der Bruchmechanik
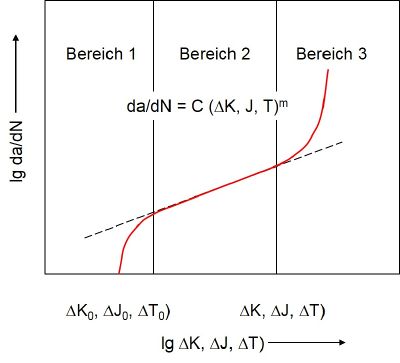
Eine schematische Darstellung einer aus einem zyklischen Bruchmechanikversuch resultierenden Risswachstumskurve ist in Bild 2 gezeigt. Eine Risswachstumskurve zeigt die doppeltlogarithmische Darstellung der Abhängigkeit der Risswachstumsgeschwindigkeit von einer bruchmechanischen Zähigkeitskenngröße wie K, J oder im Fall der Elastomerprüfung T. Die Risswachstumsgeschwindigkeit entspricht der Änderung der Risslänge Δa in Abhängigkeit von der Zykluszahl N und wird meist in differentieller Form da/dN angegeben. Wie aus Bild 2 hervorgeht, können aus einer solchen Risswachstumskurve zwei bruchmechanische Kennwerte abgeleitet werden: ein Schwellwert und ein kritischer Wert der jeweiligen bruchmechanischen Kenngröße. Im Bereich 1 besteht ähnlich wie im Bereich 3 ein großer Einfluss der Mikrostruktur, der Mittelspannung und von möglichen Umgebungsmedien. Letzteres bedeutet für Elastomere, dass unterhalb der Schwellreißenergie T0 die Rissausbreitung nur in Anwesenheit von Ozon stattfindet [10].
| Bild 2: | Risswachstumskurve in Anlehnung an [10, 11] |
Der Bereich 2 ist bei doppeltlogarithmischer Auftragung durch einen nahezu linearen Zusammenhang zwischen der bruchmechanischen Kenngröße und der Risswachstumsgeschwindigkeit gekennzeichnet, welcher mit der Paris-Erdogan-Beziehung nach Gl. (1) beschrieben werden kann [11, 12]:
| (1) |
mit:
C, m – werkstoffspezifische Konstanten
Bei einem Anstieg der Belastungsgröße über einen kritischen Wert geht der Bereich 2 in den Bereich 3 über, wobei ein starker Anstieg der Rissausbreitungsgeschwindigkeit da/dN zu verzeichnen ist, d. h., hier findet ein Übergang von stabiler Rissausbreitung in die beschleunigte stabile oder in die instabile Rissausbreitung statt.
Risswachstumsverhalten der Elastomere
In zahlreichen Untersuchungen [12‒15] wurde nachgewiesen, dass eine große Anzahl der untersuchten Elastomerwerkstoffe den in Bild 2 dargestellten theoretischen Kurvenverlauf der Risswachstumskurve zeigen. Der Aufbau der Elastomere und demnach auch deren Struktur haben neben vielen physikalischen Eigenschaften auch einen Einfluss auf das Risswachstumsverhalten. Es finden sich in der Literatur zahlreiche Studien, die sich mit der Bewertung des Ermüdungsrissverhaltens in Bezug auf die Werkstoffzusammensetzung beschäftigen. Papadopoulos et al. [16] untersuchten beispielsweise für SBR- und NR-Vulkanisate den Einfluss des Rußgehaltes auf das dynamische Risswachstumsverhalten unter Verwendung von Pure Shear-Prüfkörpern. Der Vergleich der Risswachstumskurven zeigte dabei, dass für die NR-Vulkanisate unter den gewählten experimentellen Bedingungen eine wesentlich kleinere Rissausbreitungsgeschwindigkeit bei vergleichbarer Reißenergie T gegeben war als für die SBR-Vulkanisate. Die Füllstoffzugabe resultierte ebenfalls in einer Verringerung der Rissausbreitungsgeschwindigkeit.
Rußverstärkte NR- und HNBR-Vulkanisate wurden auch von Kim et al. [17] untersucht. Sie verwendeten ebenfalls Pure Shear-Prüfkörper für die zyklischen Bruchmechanikversuche an rußverstärkten NR- und HNBR-Werkstoffen. Die Prüfkörper wurden mit unterschiedlichen Amplituden zwischen 25 und 200 % mit einer Frequenz von 1 Hz beansprucht. Die Zyklenzahl war mit 10.000 festgelegt und die Bestimmung der Rissgröße erfolgte nach dem Versuch. Aus diesen Daten wurde die Risswachstumsgeschwindigkeit ermittelt. Als Füllstoffe kamen Ruße mit unterschiedlichen Aktivitäten zur Anwendung. Die Ergebnisse der bruchmechanischen Untersuchungen der NR-Vulkanisate zeigten dabei, dass die Mischungszusammensetzung insbesondere hinsichtlich des Füllstoffanteils einen wesentlichen Einfluss auf Risswachstumsgeschwindigkeit bei vergleichbarer Größe der Energiefreisetzungsrate hat. Der Füllstofftyp hat sich unter den gewählten Untersuchungsbedingungen nicht sehr stark auf die Risswachstumskurven der NR-Werkstoffe ausgewirkt.
Ebenfalls zyklische Bruchmechanikversuche führten Yuanbo Liu et al. [18] durch. Das Ziel war die Bewertung des Einflusses des Füllstoffes bzw. Füllstoffsystems basierend auf Ruß und organisch modifiziertem Montmorillonit auf die mechanischen und bruchmechanischen Eigenschaften. Für die zyklischen Bruchmechanikversuche wurden metallklingengekerbte SENT-Prüfkörper verwendet und es wurden maximale Dehnungen von 30 % aufgebracht. Die Beanspruchung war sinusförmig und erfolgte mit einer Frequenz von 3 Hz. Im Ergebnis der Untersuchungen wurde gezeigt, je geringer der Anstieg m der Risswachstumskurve im Bereich 2 ist, desto größer ist vergleichsweise der Widerstand gegen Ermüdungsrissausbreitung. Mit den Untersuchungen haben die Autoren u. a. gezeigt, dass sich eine Füllstoffkombination aus Ruß und OMMT positiv auf den Anstieg m auswirken kann, d. h. der Ermüdungsrisswiderstand wird größer, obwohl es gleichzeitig zu einer Erhöhung der Risswachstumsgeschwindigkeit bei vergleichbarer Reißenergie kommt. Als Ursache werden zusätzliche energiedissipierende Prozesse durch das Vorhandensein der OMMT-Schichten diskutiert.
Literaturhinweise
| [1] | Reincke, K.: Elastomere Werkstoffe – Zusammenhang zwischen Mischungsrezeptur, Struktur und mechanischen Eigenschaften sowie dem Deformations- und Bruchverhalten, Habilitation, Martin-Luther-Universität Halle-Wittenberg, Shaker Verlag (2016) (ISBN 978-3-8440-4637-3; siehe AMK-Büchersammlung unter B 2-2) |
| [2] | Eisele, U., Kelbch, S., Engels, H.‐W.: The Tear Analyzer – A New Tool for Quantitative Measurements of the Dynamic Crack Growth of Elastomers. Kautsch. Gummi Kunstst. 45 (1992) 1064–1069 |
| [3] | Krause, K.‐H., Mennig, G.: Ermüdungsprüfung an Gummi. Tagungsband TECHNOMER 99, Chemnitz (1999) (ISBN 3-00-004710-7) |
| [4] | Stoček, R., Gehde, M., Heinrich, G.: Analyse des dynamischen Risswachstums von Elastomeren−Simultaner Zug‐(Tensile‐) und Pure‐Shear‐Prüfmodus bei optimierter Risserfassung. Kautsch. Gummi Kunstst. 62 (2009) 170–176 |
| [5] | Stoček, R., Heinrich, G., Gehde, M.: The Influence of the Test Properties on Dynamic Crack Propagation in Filled Rubbers by Simultaneous Tensile‐ and Pure‐Shear‐Mode Testing. In: Heinrich, G., Kaliske, M., Lion, A., Reese, S., (Eds.): Constitutive Models for Rubber VI, CRC Press (2009) 345–352 |
| [6] | Krause, K.‐H.: Gepulste Risswachstums‐Prüfungen an Gummiwerkstoffen. TECHNOMER 97, Chemnitz (1997) (ISBN 3-00-001942-1) |
| [7] | Ziegler, C., Baaser, H., Häusler, O.: Fatigue and Crack Growth Behavior of Rubber Products. In: Boukamel, A., Laiarinandrasana, L., Méo, S., Verron, E. (Eds.): Constitutive Models for Rubber V, Taylor & Francis Group London (2008) 197–202 |
| [8] | Stoček, R.: Dynamische Rissausbreitung in Elastomerwerkstoffen. Dissertation, Technische Universität Chemnitz (2012) |
| [9] | https://www.coesfeld.com/produkte/d/elastomerpruefung/dynamisch.html; (Zugriff am 22.01.2023) |
| [10] | Clamroth, R., Eisele, U.: Untersuchungen zur Weiterreißfestigkeit und Beständigkeit gegen Rissbildung. Kautsch. Gummi Kunstst. 28 (1975) 433–440 |
| [11] | Blumenauer, H.: Werkstoffprüfung. 6. Auflage, Deutscher Verlag für Grundstoffindustrie, Leipzig (1994) (ISBN 3-342-00547-5; siehe AMK-Büchersammlung unter M 3) |
| [12] | Eisele, U.: Introduction to Polymer Physics. Springer, Berlin Heidelberg (1990) (ISBN 978-3-642-74436-5) |
| [13] | Stevenson, A.: Fatigue and Fracture of Rubber in Engineering Applications. Paper for Educational Symposium. 145th Technical Meeting of the Rubber Division, ACS, Chicago April 19–22, 1994 |
| [14] | Aglan, H., Moet, A.: The Resistance of Rubber Compounds to Brittle Crack Propagation. Rubber Chem. Technol. 62 (1989) 98–106 |
| [15] | Young, D. G., Danik, J. A.: Effects of Temperature on Fatigue and Fracture. Rubber Chem. Technol. 67 (1994) 137–147 |
| [16] | Papadopoulos, I. C., Thomas, A. G., Busfield, J. J. C.: Rate Transitions in the Fatigue Crack Growth of Elastomers. J. Appl. Polym. Sci. 109 (2008) 1900–1910 |
| [17] | Wonho Kim, Minyoung Kim, Young‐Wook Chang, Jung‐Eun Shin, Jong‐Woo Bae: Fatigue Crack Growth Behavior of NR and HNBR Based Vulcanizates with Potential Application to Track Pad for Heavy Weight Vehicles. Macromol. Res. 11 (2003) 73–79 |
| [18] | Yuanbo Liu, Li Li, Qi Wang, Xin Zhang: Fracture Properties of Natural Rubber Filled with Hybrid Carbon Black/Nanoclay. J. Polym. Res. 18 (2011) 859–867 |