Ultraschalldoppelbrechung
| Ein Service der |
|---|

|
| Polymer Service GmbH Merseburg |
| Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de |
| Unser Weiterbildungsangebot: https://www.psm-merseburg.de/weiterbildung |
| PSM bei Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg |
Ultraschalldoppelbrechung
Allgemeines
Brechung und Doppelbrechung sind optische oder akustische Phänomene, die bei Ausbreitung von elektromagnetischen Wellen an äußeren oder inneren Grenzflächen anisotroper Werkstoffe auftreten und in engem Zusammenhang mit der Ausbreitungsgeschwindigkeit, der Strahlenoptik oder -akustik und dem Polarisationszustand zu sehen sind.
Brechung
Brechung (Refraktion) tritt bei Wellen (Licht, Schall- oder akustische Wellen, Wasserwellen oder seismischen Wellen) auf, die sich mehrdimensional in isotropen Medien oder Werkstoffen ausbreiten und deren Wellenlänge klein im Vergleich zum Ausbreitungsmedium ist. Durch die Brechung entsteht eine Änderung der Ausbreitungsrichtung infolge der räumlichen Veränderung der Ausbreitungsgeschwindigkeit (Phasengeschwindigkeit von monochromatischen Wellen), die durch die Brechzahl (auch Brechungsindex genannt) n speziell bei Lichtwellen beschrieben werden kann [1, 2].
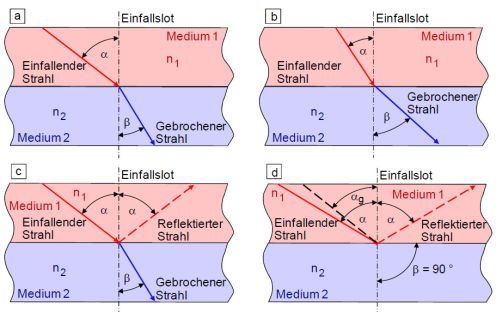
| Bild 1: | Brechung zum Lot vom optisch dünneren zum dichteren Medium a), vom Lot bei optisch dichteren zu dünnerem Medium b), Brechung und Reflexion c) und Totalreflexion an der Grenzfläche d) |
Bei den Brechungsindizes n1 < n2 tritt Brechung zum Einfallslot auf und es gilt, dass sin α > sin β und c1 > c2 sind (Bild 1a), während bei n1 > n2 Brechung weg vom Einfallslot auftritt und damit sin α < sin β und c1 < c2 sind (Bild 1b). In Abhängigkeit von den Eigenschaften der Grenzfläche tritt neben der Brechung auch Reflexion auf, so dass ein Teil des einfallenden Strahls reflektiert als auch transmittiert wird (Bild 1c). Die Brechungswinkel hängen nach dem SNELLIUS'schen Brechungsgesetz vom Verhältnis der Brechungsindizes ab (Gl.1).
| Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{n_{1}}{n_{2}}=\frac{sin \alpha }{sin \beta}} | (1) |
Infolge dieses Zusammenhangs kann die Richtungsänderung von Strahlen beim Übergang in ein Medium mit anderer Dichte bzw. Phasengeschwindigkeit begründet werden, woraus aber kein Transmissions- bzw. Reflexionsfaktor abgeleitet werden kann. Wird der Einfallswinkel größer als der Grenzwinkel der Totalreflexion (gestrichelte schwarze Linie in Bild 1d), dann erfolgt keine Brechung, da der Brechungswinkel ein Maximum von 90 ° besitzt. In diesem Fall hat der reflektierte Strahl die gleiche Intensität wie der einfallende Strahl und der Reflexionsfaktor ist 1. In der Optik nutzt man diese Eigenschaft zu Richtungsänderungen im Strahlengang (Umlenkprismen) und in der Akustik bzw. Ultraschallprüfung beruhen die Winkel-Prüfköpfe zur Prüfung mit Transversalwellen auf diesem Effekt. Unter dem Reflexions- und Transmissionsfaktor versteht man vereinfacht in der Akustik das Amplitudenverhältnis von reflektierter zu einfallender Welle bzw. transmittierter zu einfallender Welle, wobei eine Abhängigkeit vom Typ der Welle (Longitudinal oder Transversal) und dem Einfallswinkel besteht. In der Optik beschreiben die FRESNEL'schen Formeln ebenfalls den von der Polarisation abhängigen Transmission- und Reflexionsfaktor und man erhält durch Quadrieren des SNELLIUS'schen Brechungsgesetzes den Transmissions- (T) und Reflexionsgrad (R), welche das Intensitäts- oder Energieverhältnis der beiden Wellen I/I0 darstellen [2−4].
In der Ultraschallprüfung mit Normalprüfköpfen werden zumeist Longitudinalwellen genutzt, bei der die Schallwellen senkrecht auf eine Grenzfläche auftreffen (Bild 2).
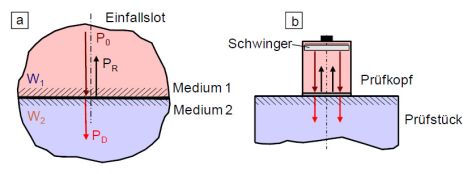
| Bild 2: | Schallausbreitung durch eine Grenzfläche bei Nutzung von Longitudinalwellen a), und bei Verwendung eines Normalprüfkopfs b) |
Trifft eine Schallwelle mit dem Schalldruck P0 aus einem Medium mit der Schallkennimpedanz W1 auf eine Grenzfläche mit der Impedanz W2, dann wird ein Teil der Schallwelle reflektiert und ein Part wird durchgelassen. Die Schallkennimpedanz ergibt sich nach Gl. (2) aus dem Produkt der Dichte ρ und der Schallgeschwindigkeit c des jeweiligen Mediums. Die reflektierte Schallwelle weist den Schalldruck PR und
| Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle W = \rho \ c \!} | (2) |
die transmittierte Welle hat den Schalldruck PD. Aus den Schallkennimpedanzen ergibt sich dann der Reflexionsfaktor R (Gl. 3) und der Transmissions- oder Durchlässigkeitsfaktor T nach der Gl. (4).
| Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle R=\frac{W_{2}-W_{1}}{W_{2}+W_{1}}} | (3) |
| Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle T=\frac{2W_{2}}{W_{2}+W_{1}}} | (4) |
Bei senkrechtem Auffall von Schallwellen auf ebene Grenzflächen tritt also keine Wellenumwandlung auf und bei identischen Medien (W1 = W2) wird R = 0 und T =1, d. h. es existiert ein ungehinderter Schalldurchtritt.
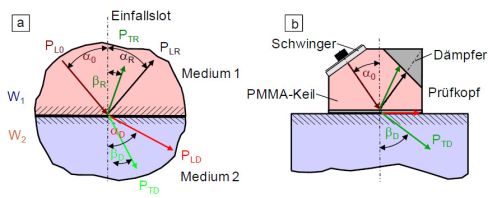
Bei schrägem Eintritt von Longitudinalschallwellen auf ebene Grenzflächen zwischen zwei festen Medien tritt eine Wellenumwandlung infolge Reflexion, Brechung und Aufspaltung der Welle auf (Bild 3) [5, 6]. Die Brechungswinkel der Longitudinalwelle und der Transversallwellen im Medium 1 und 2 berechnen sich entsprechend des SNELLIUS'schen Brechungsgesetzes (Bild 3a), wobei die Amplituden entstehenden Wellenarten winkelabhängig sind. Wird abhängig von den Eigenschaften der Medien der Winkel α0 so groß gewählt, dass der Brechungswinkel der Longitudinalwelle größer als 1 ist, dann existiert im Medium 2 nur noch die abgespaltene Transversalwelle. Diese Eigenschaft wird bei den Winkel-Prüfköpfen technisch z. B. bei der Schweißnahtprüfung genutzt (Bild 3b).
| Bild 3: | Schallausbreitung an schrägen Grenzflächen und Entstehung von Transversalwellen a), und Anwendung bei Winkelprüfköpfen b) |
Doppelbrechung
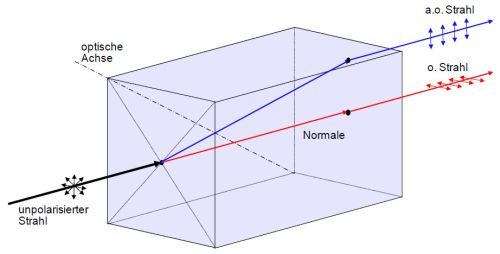
Bei anisotropen Materialien, wie Kristallen, tritt Doppelbrechung oder Birefringenz auf. Das bedeutet, dass die Anteile einer optischen oder akustischen Welle in Abhängigkeit von ihrer Polarisation mit unterschiedlichen Winkeln gebrochen werden, wodurch zwei senkrecht zueinander polarisierte Teilwellen entstehen. Diese Teilwellen weisen unterschiedliche Brechungsindizes no und nao, der ordentlichen und außerordentlichen Welle auf, wobei der Brechungsindex der ordentlichen Welle oder des optischen Strahls unabhängig von der Ausbreitungsrichtung ist (Bild 4) [2]. Bei der außerordentlichen Welle hängt der Brechungsindex von der Ausbreitungsrichtung ab.
Das heißt, dass für den ordentlichen Strahl oder die Welle das SNELLIUS'sche Brechungsgesetz der isotropen Materialien gilt, aber für den außerordentlichen Strahl nicht, der selbst bei senkrechtem Einfall in ein doppelbrechendes Material gebrochen wird. Damit haben die Wellenfronten dieser beiden Strahlen auch differierende Ausbreitungsgeschwindigkeiten. Die Differenz Δn = nao – no ist das Maß der Doppelbrechung, wobei das Vorzeichen von Δn die optische Orientierung darstellt und das Verhältnis der Ausbreitungsgeschwindigkeiten des ordentlichen und außerordentlichen Strahls beschreibt.
| Bild 4: | Aufspaltung in einen ordentlichen und außerordentlichen Strahl bei Doppelbrechung |
In der Optik nutzt man doppelbrechende Prismen zur linearen Polarisation von Licht, wodurch die Nutzung von variablen Strahlteilern ermöglicht wird.
Andererseits kann Doppelbrechung auch bei isotropen Materialien auftreten, wenn elektrische oder magnetische Felder einwirken oder mechanische Spannungen bei Werkstoffen die sogenannte Spannungsdoppelbrechung hervorrufen (Spannungsoptik oder Polarisationsmikroskopie für Last- oder Eigenspannungen). Wird bei der Polarisationsmikroskopie oder der Spannungsoptik an Kunststoffbauteilen eine Drehung der Probe zwischen gekreuzten Polarisationsfiltern durchgeführt, dann verändert sich die Helligkeit oder die Farbe des doppelbrechenden und mit Eigenspannung behafteten Teils, während optisch isotrope Materialien (z. B. getemperte Kunststoffe) keine Veränderungen im Bild aufweisen.
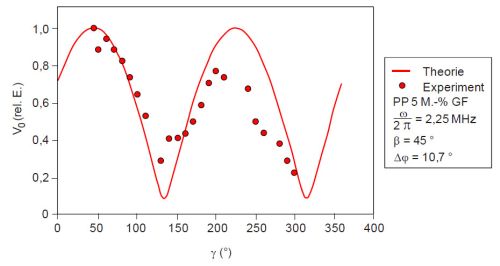
Akustische Transversalwellen breiten sich im isotropen Festkörper unabhängig von der Ausbreitungs- und Polarisationsrichtung aus, d. h. eine ebene akustische Transversalwelle ist nur dann linear polarisiert, wenn ihre Polarisationsrichtung mit einer Hauptrichtung identisch ist. In Analogie zur optischen Doppelbrechung bezeichnet man diesen Effekt als akustische Doppelbrechung, d. h. beim Auftreten eines Spannungsfelds im Werkstoff ist die Ausbreitung der Transversalwelle nicht mehr von der Ausbreitungs- und Polarisationsrichtung unabhängig [7], wodurch die Analyse der Ausbreitungsgeschwindigkeiten für die Bewertung des Spannungs- oder Anisotropiezustandes an metallischen [8, 9] und polymeren [10, 11] Verbundwerkstoffen genutzt werden kann. Bei faserverstärkten Kunststoffen kann die auftretende akustische Anisotropie zur Detektion der Vorzugs- oder Hauptorientierungsrichtung verwendet werden [12]. Wird die Richtungsabhängigkeit der Tangentialwellen in Abhängigkeit vom Drehwinkel des Empfängers aufgetragen, dann kann man die Faserorientierung der Kurzglasfasern zerstörungsfrei nachweisen (Bild 5).
| Bild 5: | Akustische Anisotropie einer 4 mm dicken spritzgegossenen Polypropylen Platte mit 5 M.-% Kurzglasfasern (Kurzzeichen: PP): Ultraschallamplitude V0 als Funktion des Empfängerwinkels [12] |
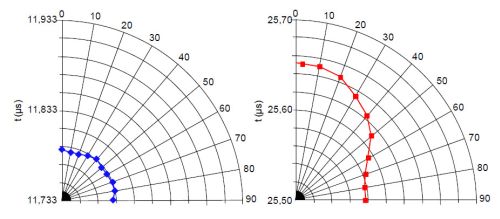
Mit diesem Verfahren lassen sich auch Texturen an metallischen Werkstoffen, die durch die Herstellung (Walzen, Tiefziehen) entstanden sind, untersuchen. Werden z. B. Rohre aus gewalzten Stahlblechen hergestellt, dann ergeben sich deutliche Eigenschaftsunterschiede in Walz- und Querrichtung, die durch das orientierte Gefüge hervorgerufen werden. Diese Effekte werden anhand der Unterschiede der Ultraschall-Laufzeiten von Longitudinal- und Transversalwellen an einem spannungsarm geglühten Rohrwerkstoff ersichtlich (Bild 6) [13].
| Bild 6: | Richtungsabhängigkeit der Laufzeiten von Longitudinalwellen (links) und Transversalwellen (rechts) nach [13] |
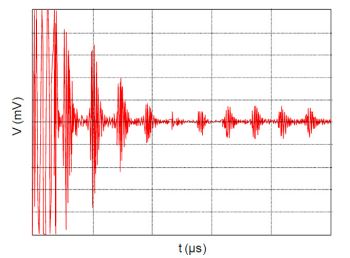
Bei starken Walztexturen tritt akustische Doppelbrechung von Transversalwellen auf, welche in speziellen Ausbreitungsrichtungen durch Interferenz der unterschiedlich polarisierten Ultraschallwellen das in Bild 7 dargestellte typische Signalbild hervorruft [13].
| Bild 7: | HF-Bild bei Doppelbrechung von Transversalwellen nach [13] |
Literaturhinweise
| [1] | Recknagel, A.: Physik – Schwingungen und Wellen, Wärmelehre. Huss-Medien Verlag, Berlin, 16. Auflage (1990), (ISBN 978-3341009826) |
| [2] | Eichler, J., Eichler, H. J.: Laser – Bauformen, Strahlführung, Anwendungen. Springer Verlag, Berlin, 5. Auflage (2003), (ISBN 3-540-00376-2) |
| [3] | Demtröder, W.: Experimentalphysik – Band 2: Elektrizität und Optik. Springer Verlag, Berlin, 3. Auflage (2004), (ISBN 3-540-20210-2) |
| [4] | Demtröder, W.: Laserspektroskopie – Band 1: Grundlagen. Springer Verlag, Berlin, 6. Auflage (2014), (ISBN 978-3-642-21305-2) |
| [5] | Deutsch, V., Platte, M., Vogt, M.: Ultraschallprüfung – Grundlagen und industrielle Anwendungen. Springer Verlag, Berlin, (1997), (ISBN 3-540-62072-9) |
| [6] | Matthies, K.: Dickenmessung mit Ultraschall. DVS-Verlag GmbH, Berlin, 2. Auflage (1998), (ISBN 3-87155-940-7) |
| [7] | Längler, F.: Wissensbasierte Automatisierung und kontinuumsmechanische Erweiterung der Ultraschall-Eigenspannungsanalyse zur Beschreibung des Spannungszustands im gesamten Bauteil. Dissertation (2007), Universität des Saarlands |
| [8] | Allen, D. R., Sayers, C. M.: The Measurement of Residual Stress in Textured Steel using an Ultrasonic Velocity Combinations Technique. Ultrasonics 22, (1984) 179–188 |
| [9] | Schneider, E.: Ultrasonic Birefringence Effect – Its Application for Materials Characterizations. Optics and Lasers in Engineering 22 (1995) 305–323 |
| [10] | Rheinfurth, M., Döring, D., Solodov, I., Busse, G.: Zweierlei Ultraschallverfahren zur zerstörungsfreien Messung der elastischen Anisotropie in faserverstärkten Polymerwerkstoffen. DGZfP-Jahrestagung, Erfurt 2010 |
| [11] | Weikert, M., Niese, F., Szielasko, K.: Neue Ansätze zur Charakterisierung hochfester Stähle mittels geführter Ultraschallwellen. DGZfP-Jahrestagung, Potsdam 2014 |
| [12] | Busse, G.: Zerstörungsfreie Kunststoffprüfung. In: Grellmann, W., Seidler, S. (Hrsg.): Kunststoffprüfung. Carl Hanser Verlag, München (2015) 3. Auflage, S. 461–528 (ISBN 978-3-446-44350-1; siehe AMK-Büchersammlung unter A 18) |
| [13] | Pohl, J., Hildebrand, J., Diemar, A., Großmann, A.: Spannungsmessung an druckbeanspruchten Stahlrohren mittels Ultraschall- und röntgenografischen Verfahren. DGZfP-Jahrestagung, Graz 2012 |