VOIGT-KELVIN-Modell
| Ein Service der |
|---|

|
| Polymer Service GmbH Merseburg |
| Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de |
| Unser Weiterbildungsangebot: https://www.psm-merseburg.de/weiterbildung |
| PSM bei Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg |
VOIGT-KELVIN-Modell
Analogiemodelle
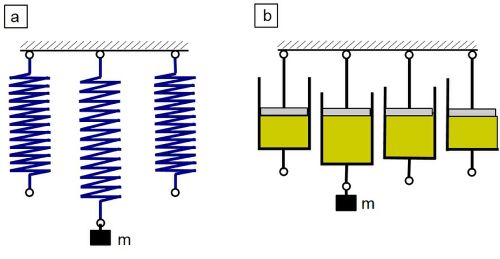
Das linear-viskoelastisches Verhalten von Kunststoffen ist näherungsweise im Modell durch die mathematische Kombination von linear-elastischen und linear-viskosen Prozessen darstellbar (siehe auch: Deformation). In der Mechanik verwendet man zur besseren Beschreibung mechanische oder elektrische Analogiemodelle. Dabei wird für das elastische Verhalten eine Feder und für das viskose Verhalten ein Dämpfer verwendet (Bild 1).
Die lineare Viskoelastizität ist allerdings exakt nur für den Bereich infinitesimal kleiner Beanspruchungen definiert. Die Werkstoffeigenschaften sind dann nur von der Zeit, nicht jedoch von der Höhe der mechanischen Belastung abhängig.
Der elastische Anteil (HOOKE’sche Feder: Bild 1a) bewirkt eine spontane, begrenzte, reversible Verformung (siehe auch: HOOKE’sches Gesetz), während der viskose Anteil (NEWTON’scher Dämpfer: Bild 1b) grundsätzlich eine zeitabhängige, unbegrenzte, irreversible Deformation hervorruft. Der viskose und elastische Anteil ist bei verschiedenen viskoelastischen Kunststoffen jeweils unterschiedlich stark ausgeprägt und die Art des Zusammenwirkens der beiden Anteile differiert. Das viskoelastisches Verhalten kann also durch die Kombination zweier oder mehrerer dieser Elemente modelliert werden [1].
| Bild 1: | Federmodell (a) und Dämpfermodell (b) der linearen Viskoelastizität |
Bei Belastung der Feder entsteht spontan eine Verlängerung, die sich bei Entlastung verzögerungsfrei auf die Ausgangslänge zurückstellt. Bei linearem energieelastischem Verhalten zwischen Federkraft und Verlängerung bzw. Spannung und Dehnung ist eine vollständige Beschreibung durch das HOOKE’sche Gesetz (Gl.1) möglich.
| (1) |
Der Dämpfer für NEWTON’sche Flüssigkeiten beschreibt das rein viskose Verhalten, welches wesentlich von der Viskosität η abhängig ist (Gl. 2). Die entstehende Spannung am Dämpfer wird bei konstanter Viskosität nur von der Deformationsgeschwindigkeit bzw. der Dehnrate dε/dt bestimmt.
| (2) |
Die Parallelschaltung der beiden Elemente (Feder und Dämpfer) ergibt das MAXWELL-Modell (Bild 2). Bei einer Belastung verformt sich die Feder unverzüglich, bei gleichzeitiger zeitabhängiger und unbegrenzter viskoser Verformung, die von der Viskosität abhängig ist. Bei einer Belastung durch die Masse m wird die Verformung durch den Dämpfer gebremst. Nach Entlastung bewegt sich die Feder zurück und der verbleibende viskose Spannungsanteil stellt sich in Abhängigkeit von der Zeit zurück. Es liegt demzufolge auch hier eine zeitabhängige, unbegrenzte, irreversible Verformung wie bei einer Flüssigkeit vor, allerdings gibt es auch einen zeitunabhängigen und reversiblen spontanelastischen Anteil wie bei einem Festkörper.
VOIGT-KELVIN-Modell
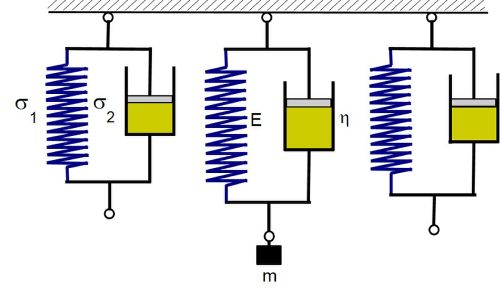
Das VOIGT-KELVIN-Modell stellt den einfachsten Modellansatz zur Beschreibung des Retardations- oder Kriechverhalten von Kunststoffen dar [2], der auf der Parallelschaltung von elastischen und viskosen Deformationsanteilen und der Summation der Spannungsanteile σ1 und σ2 beruht (Gl. 3).
| Bild 2: | Deformationsverhalten des VOIGT-KELVIN-Modells (Retardationsverhalten) |
| (3) |
Setzt man die die Gl. (1) sowie Gl. (2) in die Gl. (3) ein, dann erhält man die mathematische Beschreibung für den VOIGT-KELVIN-Körper (Gl. 4).
| (4) |
Für die Retardation gilt σ = σ0 = konst., so dass dσ/dt = 0 wird und die Dehnung ε nur von der Zeit abhängt.
Kriechverhalten Kunststoffe
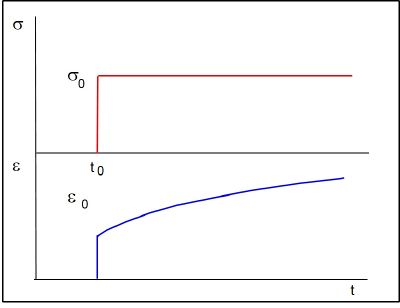
Aus Gl. (4) ergibt sich eine inhomogene lineare Differentialgleichung (Gl. 5), deren Lösung die Gl. (6) ist und eine einfache Beschreibung des Kriechverhaltens von Kunststoffen erlaubt (Bild 3).
| (5) |
| (6) |
Der Quotient η/E entspricht der Zeitkonstante bzw. Retardationszeit τret, die angibt nach welcher Zeit die Dehnung ε um den e-ten Teil der Ausgangdehnung ε0 zugenommen hat.
| Bild 3: | Zeitverhalten des VOIGT-KELVIN-Modells (Retardationsverhalten) |
Mit einer einzigen Retardationszeit ist das VOIGT-KELVIN-Modell allerdings nur unzureichend in der Lage, das komplexe Kriechverhalten realer Kunststoffe zu beschreiben.
Literaturhinweise
| [1] | Lüpke, T.: Grundlagen mechanischen Verhaltens. In: Grellmann, W., Seidler, S. (Hrsg.): Kunststoffprüfung. Carl Hanser Verlag, München (2015) 3. Auflage S. 91/92, (ISBN 978-3-446-44350-1; siehe AMK-Büchersammlung unter A 18) |
| [2] | Bierögel, C.: Biegeversuch an Kunststoffen. In: Grellmann, W., Seidler, S. (Hrsg.): Kunststoffprüfung. Carl Hanser Verlag, München (2015) 3. Auflage, S. 147–158 (ISBN 978-3-446-44350-1; siehe AMK-Büchersammlung unter A 18) |