Klebverbindungen – Kennwertermittlung

Ein Service der

Polymer Service GmbH Merseburg
Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de
Unser Weiterbildungsangebot: https://www.psm-merseburg.de/weiterbildung
PSM bei Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg

Klebverbindungen – Kennwertermittlung (Autor: Prof. Dr.-Ing. Stephan Marzi)

Ermittlung von bruchmechanischen Kennwerten an DCB-Prüfkörpern für Klebverbindungen

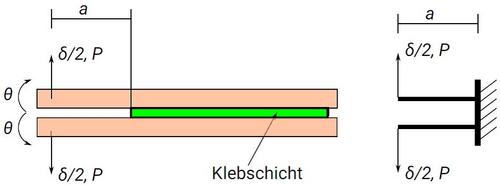
Der DCB-Prüfkörper wird ‒ wie in Bild 1 skizziert ‒ bevorzugt zur Bestimmung der (kritischen) Energiefreisetzungsrate G_Ic im Mode I eingesetzt. Es finden sich jedoch auch Arbeiten, bei denen DCB-Prüfkörper im Mode III [1] oder im Mixed-Mode I+III [2, 3] genutzt werden.

Der DCB-Prüfkörper besteht aus zwei balkenförmigen Fügeteilen (o. a. Substraten), die sich während des Versuchs nur linear-elastisch deformieren dürfen und mit dem zu untersuchenden Klebstoff gefügt werden. Im Gegensatz zu den zuvor genannten Auswerteverfahren, die auf singulären Spannungsfeldern an der Rissspitze und dem dazugehörigen Konzept der Spannungsintensitätsfaktoren beruhen, werden im Falle von Klebverbindungen üblicherweise Verfahren nach der Balkentheorie herangezogen. Näheres hierzu ist normativ in ISO 25217 [4] geregelt.

Bild 1:

Skizze und Nomenklatur eines DCB-Versuchs an Klebverbindungen (links) und Ersatzmodell (rechts)

Die Verfahren zur Balkentheorie basieren auf der Irwin-Kies-Gleichung,

G_{Ic}={\frac {P^{2}}{2B}}{\frac {dC}{da}}

(1)

mit der Probennachgiebigkeit C ≡ δ/P und der aktuellen Risslänge a, und beruhen somit auf der linear-elastischen Bernoullischen Balkentheorie. Insbesondere impliziert die Irwin-Kies-Gleichung ferner, dass

die Kraft-Weg (P-δ)-Kurve im Falle einer Entlastung linear und durch den Ursprung verläuft,
der Klebstoff sich unendlich steif und ideal-spröde verhält,
die Risslänge a groß genug ist (a/h > 10) um das Ersatzmodell zweier Kragträger der Länge a verwenden zu können, und
die beiden Kragträger an der aktuellen Rissposition als fest eingespannt betrachtet werden können.

Einfache Balkentheorie / Simple Beam Theory (SBT)

Die einfache Balkentheorie (engl. Simple Beam Theory, SBT) geht davon aus, dass die oben genannten Voraussetzungen zutreffen. In diesem Falle reduziert sich die Irwin-Kies-Gleichung auf

G_{Ic}={\frac {4P^{2}}{E_{S}H^{2}}}\left({\frac {3a^{2}}{h^{3}}}+{\frac {1}{h}}\right)

(2)

Hierin sind B, h und E_S die Breite, die Höhe und der Elastizitätsmodul eines Fügeteils. In der Realität sind Klebstoffe verglichen zu den Fügeteilen (Substraten) deutlich weicher und nachgiebiger und können somit nicht als unendlich steif betrachtet werden. Folglich liegt meist keine feste Einspannung an der Position der Rissspitze vor und Gl. (2) unterschätzt die Energiefreisetzungsrate.

Korrigierte Balkentheorie / Corrected Beam Theory (CBT)

Zur Bestimmung korrekter Energiefreisetzungsraten empfiehlt ISO 25217 [4] die Verwendung einer modifizierten Form von Gl. (2), bei der die Risslänge a um eine Einspannungs-Korrekturlänge Δ korrigiert wird,

G_{Ic}={\frac {4P^{2}}{E_{S}H^{2}}}\left({\frac {3(a+\Delta )^{2}}{h^{3}}}+{\frac {1}{h}}\right)

(3)

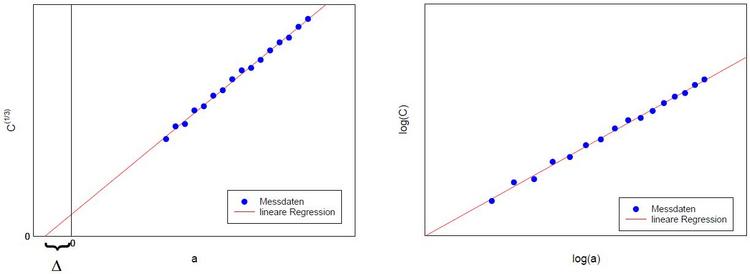
um der Nachgiebigkeit der Einspannung im Ersatzmodell Rechnung zu tragen. Die Korrekturlänge Δ lässt sich dabei experimentell über eine Nachgiebigkeitskalibrierung bestimmen und folgt direkt aus einer linearen Regression zwischen C^1/3 und a, wie Bild 2 (links) verdeutlicht.

Bild 2:

Nachgiebigkeitskalibrierung: CBT (links) und ECM (rechts)

Experimentelle Nachgiebigkeitsmethode / Experimental Compliance Method (ECM)

Alternativ zur korrigierten Balkentheorie (CBT) kann auch die experimentelle Nachgiebigkeitsmethode (engl. Experimental Compliance Method (ECM)) verwendet werden, die 1963 von Berry [5] vorgeschlagen wurde und auch unter dem Namen Berry’s Method geläufig ist. Während die CBT das Balkenmodell durch eine Anpassung der Kraglänge kalibriert und somit physikalisch anschaulich bleibt, stützt sich die ECM auf eine Kalibrierung der Ordnung n, mit der die Nachgiebigkeit C von der Risslänge a abhängt, C ∝ aⁿ. Die Irwin-Kies-Gleichung nimmt dann die Form

G_{Ic}={\frac {nP\delta }{2Ba}}

(4)

an. Der Exponent n lässt sich in ähnlicher Weise wie die Korrekturlänge Δ (CBT) über eine Nachgiebigkeitskalibrierung bestimmen und ergibt sich aus der Steigung einer linearen Regression zwischen log(a) und log(C), wie Bild 2 (rechts) illustriert.

Auswertung über Rotationsmessung (J-Integral)

Die Auswertung der Energiefreisetzungsrate G_Ic auf Basis der Gln. (2), (3) und (4) erfordert im Experiment eine Bestimmung der aktuellen Anrisslänge. Diese erfordert im Regelfall einen erhöhten Aufwand im Messaufbau und unterliegt oftmals auch einer subjektiven Bewertungen und Ungenauigkeiten (z. B. bei der visuellen Analyse von Bildaufnahmen). Wählt man die Rotation θ = 3δ/4a des Krafteinleitungspunktes als Maß für die Deformation des Prüfkörpers, dann vereinfacht sich die Irwin-Kies-Gleichung zu

G_{Ic}={\frac {2P\theta }{B}}

(5)

und hängt nur noch von der Kraft P und der Rotation θ der Krafteinleitungspunkte ab. Dieses Vorgehen erfordert zwar weitere Sensorik zur Rotationsmessung, allerdings ist keine Nachgiebigkeitskalibrierung mehr erforderlich und die Energiefreisetzungsrate lässt sich direkt aus den Messgrößen P und Θ berechnen. Die Energiefreisetzungsrate wird, sofern sie nach Gl. (5) berechnet wird, in der Regel als J_Ic bezeichnet, da sich Gl. (5) auch auf einem alternativen Wege finden lässt und dann dem J-Integral nach Rice [6] entspricht.

Da diese Auswertemethode ohne Kenntnis der Rissposition und der Biegesteifigkeit auskommt, kann (G_Ic) auch als Regelgröße verwendet werden, sofern der Regler der Materialprüfmaschine dies technisch zulässt [7]. Sollte keine Rotationsmessung möglich sein, lässt sich eine solche Regelung durch Verwendung der Gleichung

G_{Ic}=\left({\frac {3}{2}}\right)^{\frac {2}{3}}{\frac {P^{\frac {4}{3}}\delta ^{\frac {2}{3}}}{(EI)^{\frac {1}{3}}B}}

(6)

realisieren, allerdings muss dann die Biegesteifigkeit EI aus analytischen Abschätzungen oder Kalibrierversuchen bekannt sein.

Siehe auch

Literaturhinweise

[1]	Loh, L., Marzi, S.: An out-of-plane loaded double cantilever beam (ODCB) test to measure the critical energy release rate in mode III of adhesive joints. International Journal of Adhesion and Adhesives 83 (2018) 24–30, special issue on joint design, DOI: 10.1016/j.ijadhadh.2018.02.021
[2]	Loh, L., Marzi, S.: Mixed-mode I+III tests on hyperelastic adhesive joints at prescribed mode-mixity. International Journal of Adhesion and Adhesives 85 (2018) 113–122, DOI: 10.1016/j.ijadhadh.2018.05.024
[3]	Loh, L., Marzi, S.: A mixed-mode controlled DCB test on adhesive joints loaded in a combination of modes I and III. Procedia Structural Integrity 13 (2018) 1318–1323, ECF22 ‒ Loading and Environmental effects on Structural Integrity, DOI: 10.1016/j.prostr.2018.12.277
[4]	ISO 25217 (2009-5): Adhesives – Determination of the Mode I Adhesive Fracture Energy of Structural Adhesive Joints using Double Cantilever Beam and Tapered Double Cantilever Beam Specimens
[5]	Berry, J.P.: Determination of fracture surface energies by the cleavage technique. Journal of Applied Physics 34 (1963) 1, 62–68, DOI: 10.1063/1.1729091
[6]	Rice, J.R.: A path independent integral and the approximate analysis of strain concentration by notches and cracks. Journal of Applied Mechanics 35 (1968) 2, 379–386, DOI: 10.1115/1.3601206
[7]	Schrader, P., Schmandt, C., Marzi, S.: Mode I creep fracture of rubber-like adhesive joints at constant crack driving force. International Journal of Adhesion and Adhesives 113 (2022) 103079, DOI: 10.1016/j.ijadhadh.2021.103079