Bruchmechanik: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
|||
| (18 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
< | {{PSM_Infobox}} | ||
<span style="font-size:1.2em;font-weight:bold;">Bruchmechanik</span> | |||
__FORCETOC__ | |||
== Linear-elastische Bruchmechanik == | == Linear-elastische Bruchmechanik == | ||
Die Bruchmechanik geht davon aus, dass der [[Bruch]] eines Bauteils und damit des Werkstoffes infolge der Ausbreitung von | Die Bruchmechanik geht davon aus, dass der [[Bruch]] eines [[Kunststoffbauteil|Bauteils]] und damit des Werkstoffes infolge der Ausbreitung von Anrissen auftritt. Sie untersucht die Bedingungen für die Ausbreitung von Rissen (siehe [[Rissausbreitung]]) und gestattet es, zwischen der äußeren [[Beanspruchung]], d. h. der am Bauteil oder [[Prüfkörper]] wirkenden Nennspannung, der Größe und Form der Anrisse sowie dem Widerstand des Werkstoffes gegen [[Rissausbreitung]] quantitative Zusammenhänge herzustellen. | ||
Das LEBM-Konzept beschreibt den Spannungszustand in der Nähe der [[Riss|Rissspitze]] durch den Spannungsintensitätsfaktor K (Bild 1): | Das LEBM-Konzept beschreibt den Spannungszustand in der Nähe der [[Riss|Rissspitze]] durch den Spannungsintensitätsfaktor K ('''Bild 1'''): | ||
{| | {| | ||
|- | |- | ||
|width="20px"| | |||
|width="500px" | <math>\sigma_{ij}\,=\,\frac{K}{\left( 2\, \pi \, r \right)^\frac {1}{2}} \cdot g_{ij} \cdot \left( \Theta \right)</math> | |||
|(1) | |||
|} | |} | ||
mit | |||
{| | {| | ||
|- | |- | ||
|<math>\sigma</math><sub>ij</sub> | |<math>\sigma</math><sub>ij</sub> | ||
| | |width="15px" | | ||
|Normal- bzw. Schubspannungen | |Normal- bzw. Schubspannungen | ||
|-valign="top" | |-valign="top" | ||
|r,<math>\Theta</math> | |r,<math>\Theta</math> | ||
| | | | ||
|Polarkoordinaten mit der | |Polarkoordinaten mit der [[Riss]]spitze als Ursprung | ||
|-valign="top" | |-valign="top" | ||
|g<sub>ij</sub> | |g<sub>ij</sub> | ||
| | | | ||
|dimensionslose Funktion. | |dimensionslose Funktion. | ||
|} | |} | ||
[[Datei:LEBM_1.jpg|300px]] | [[Datei:LEBM_1.jpg|300px]] | ||
{| | {| | ||
|-valign="top" | |- valign="top" | ||
|Bild 1: | |width="50px"|'''Bild 1''': | ||
|Koordinatensystem zur Beschreibung des Spannungszustandes an der Rissspitze | |width="600px" |Koordinatensystem zur Beschreibung des Spannungszustandes an der Rissspitze | ||
|} | |} | ||
Der von IRWIN [1] eingeführte Spannungsintensitätsfaktor ist gegeben durch | Der von IRWIN [1] eingeführte Spannungsintensitätsfaktor ist gegeben durch | ||
{| | {| | ||
|- | |- | ||
|width="20px"| | |||
|width="500px" | <math>K\,=\,\sigma_N\, \left( \pi\, a \right)^\frac{1}{2}</math> | |||
|(2) | |||
|} | |} | ||
mit | |||
{| | {| | ||
|- | |- | ||
|<math>\sigma</math><sub>N</sub> | |<math>\sigma</math><sub><sub>N</sub></sub> | ||
| | |width="15px" | | ||
|Nennspannung | |Nennspannung | ||
|-valign="top" | |-valign="top" | ||
|a | |a | ||
| | | | ||
|Risslänge | |[[Ausgangsrisslänge|Risslänge]] | ||
|} | |} | ||
Die endliche Geometrie eines jeden Bauteils und [[Prüfkörper|Prüfkörpers]] sowie die Rissgeometrie werden durch die Einführung einer Geometriefunktion f (a/W) berücksichtigt, womit Gl. 2 in der Form | Die endliche Geometrie eines jeden Bauteils und [[Prüfkörper|Prüfkörpers]] sowie die Rissgeometrie werden durch die Einführung einer [[Geometriefunktion]] f (a/W) berücksichtigt, womit Gl. 2 in der Form | ||
{| | {| | ||
|- | |- | ||
|width="20px"| | |||
|width="500px" | <math>K\,=\,\sigma_N\, \left( \pi\, a \right)^\frac{1}{2}\, f \left( \frac{a}{W}\right)</math> | |||
|(3) | |||
|} | |} | ||
geschrieben werden kann. Die Funktionen f (a/W) sind für eine Vielzahl von [[ | geschrieben werden kann. Die Funktionen f (a/W) sind für eine Vielzahl von [[Prüfkörper_für_bruchmechanische_Prüfungen|Bruchmechanikprüfkörpern]] berechnet worden [2, 3]. Die '''Bilder 2 und 3''' enthalten die Abmessungen von bevorzugt für [[Kunststoffe]] angewandte [[Prüfkörper]]. Für einen unendlich ausgedehnten [[Prüfkörper]] und den Grenzfall eines [[Riss]]es mit einem Kerbradius <math>\rho</math> ~ 0 ist die Geometriefunktion f (a/W) = 1. | ||
Der Spannungsintensitätsfaktor erreicht zu Beginn der instabilen [[Rissausbreitung]] einen kritischen Wert K<sub>Ic</sub>, der als Bruch- oder Risszähigkeit bezeichnet wird und die Dimension MPa mm<sup>1/2</sup> erhält. Der Index I weist auf die Mode I-Belastung hin, bei der | Der Spannungsintensitätsfaktor erreicht zu Beginn der instabilen [[Rissausbreitung]] einen kritischen Wert K<sub>Ic</sub>, der als Bruch- oder [[Risszähigkeit]] bezeichnet wird und die Dimension MPa mm<sup>1/2</sup> erhält. Der Index I weist auf die Mode I-Belastung hin, bei der | ||
[[Datei:LEBM_Tabelle_1.jpg]]<br> | [[Datei:LEBM_Tabelle_1.jpg]]<br> | ||
{| | {| | ||
|- valign="top" | |||
|width="50px"|'''Bild 2''': | |||
| | |width="600px" |Prüfkörperform [[SENB-Prüfkörper|SENB]] mit Abmessungen, den dazugehörigen Bestimmungsgleichungen zur Berechnung der Bruchzähigkeiten und der [[Geometriefunktion]]en. | ||
| | |||
| | |||
|} | |} | ||
[[Datei:LEBM_Tabelle_2.jpg]]<br> | [[Datei:LEBM_Tabelle_2.jpg]]<br> | ||
{| | {| | ||
|- valign="top" | |||
|width="50px"|'''Bild 3''': | |||
| | |width="600px" |Prüfkörperformen [[SENT-Prüfkörper|SENT]] und [[CT-Prüfkörper|CT]] mit ihren Abmessungen, den dazugehörigen Bestimmungsgleichungen zur Berechnung der Bruchzähigkeiten und den [[Geometriefunktion]]en | ||
| | |||
| | |||
|} | |} | ||
die Belastung senkrecht zur Rissfläche erfolgt. | die Belastung senkrecht zur Rissfläche erfolgt. | ||
Für diesen technisch wichtigsten Fall einer Beanspruchung lautet das Bruchsicherheitskriterium | Für diesen technisch wichtigsten Fall einer [[Beanspruchung]] lautet das [[Bruchsicherheitskriterium]] | ||
{| | {| | ||
|- | |- | ||
|width="20px"| | |||
|width="500px" | <math>K_I\,\le\, K_{Ic}</math> | |||
|(4) | |||
|} | |} | ||
wonach die Bruchsicherheit eines Bauteils gewährleistet ist, solange der kritische Wert nicht überschritten wird. | wonach die Bruchsicherheit eines [[Kunststoffbauteil|Bauteils]] gewährleistet ist, solange der kritische Wert nicht überschritten wird. | ||
Neben der einfachen [[Rissöffnung]] nach Mode I sind in Bild 1 | Neben der einfachen [[Rissöffnung]] nach Mode I sind in Bild 1 auch die [[Rissöffnungsmoden]] II und III enthalten, die bei Scher- oder Torsionsbeanspruchungen auftreten.<br> | ||
In Abhängigkeit von der Prüfkörpergeometrie bilden sich vor der [[Riss|Rissspitze]] unterschiedliche mehrachsige Spannungszustände aus. Das Bild 4 zeigt am Beispiel von PVCC und PP den Einfluss der Prüfkörperdicke auf das [[Bruchverhalten]], wobei resultierend aus dem Übergang vom ebenen Spannungszustand (ESZ) in den ebenen Dehnungszustand (EDZ) makroskopisch ein Anwachsen des Normalspannungsbruches beobachtet wird.<br> | In Abhängigkeit von der Prüfkörpergeometrie bilden sich vor der [[Riss|Rissspitze]] unterschiedliche [[Mehrachsiger Spannungszustand|mehrachsige Spannungszustände]] aus. <br> | ||
Für den Fall, dass an der Rissspitze EDZ vorliegt, wird die Bruchzähigkeit von der Prüfkörpergeometrie unabhängig. Sie gibt den Einfluss der Werkstoffstruktur, der | Das '''Bild 4''' zeigt am Beispiel von nachchlorierten PVC ([[Kurzzeichen]]: PVCC) und Polypropylen ([[Kurzzeichen]]: PP) den Einfluss der Prüfkörperdicke auf das [[Bruchverhalten]], wobei resultierend aus dem Übergang vom [[Ebener Spannungszustand|ebenen Spannungszustand (ESZ) in den ebenen Dehnungszustand (EDZ)]] makroskopisch ein Anwachsen des Normalspannungsbruches beobachtet wird.<br> | ||
Für den Fall, dass an der Rissspitze EDZ vorliegt, wird die Bruchzähigkeit von der Prüfkörpergeometrie unabhängig. Sie gibt den Einfluss der Werkstoffstruktur, der [[Geschwindigkeit]] und der Umgebungstemperatur auf die [[Zähigkeit]] wieder. | |||
[[Datei:LEBM_2.jpg|400px]] | [[Datei:LEBM_2.jpg|400px]] | ||
{| | {| | ||
|- valign="top" | |||
|width="50px"|'''Bild 4''': | |||
| | |width="600px" |Abhängigkeit der Bruchzähigkeit K<sub>c</sub>, K<sub>Ic</sub> bei Raumtemperatur von der Prüfkörperdicke bei [[Quasistatische Prüfverfahren|quasistatischer]] [[Beanspruchung]] für PVCC mit K<sub>Ic</sub> = 110 MPamm<sup>1/2</sup> (a) und für PP mit K<sub>Ic</sub> = 139 MPamm<sup>1/2</sup> (b) bei einer [[Traversengeschwindigkeit]] von v<sub>T</sub> = 8,3 • 10<sup>-4</sup> ms<sup>-1</sup> | ||
|Abhängigkeit der Bruchzähigkeit K<sub>c</sub>, K<sub>Ic</sub> bei Raumtemperatur von der Prüfkörperdicke bei quasistatischer Beanspruchung für PVCC mit K<sub>Ic</sub> = 110 MPamm<sup>1/2</sup> (a) und für PP mit K<sub>Ic</sub> = 139 MPamm<sup>1/2</sup> (b) bei einer Traversengeschwindigkeit von v<sub>T</sub> = 8,3 • 10<sup>-4</sup> ms<sup>-1</sup> | |||
|} | |} | ||
Bei linear-elastischer Betrachtungsweise erfolgt die Abschätzung der Geometriegrößen B, a und der Ligamentausdehnung (W – a) über die empirisch ermittelte Beziehung [2, 4–6] | Bei linear-elastischer Betrachtungsweise erfolgt die Abschätzung der Geometriegrößen B, a und der Ligamentausdehnung (W – a) über die empirisch ermittelte Beziehung [2, 4–6] | ||
{| | {| | ||
|- | |- | ||
|width="20px"| | |||
|width="500px" | <math>B, a, \left(W-a\right)\, \ge \, \beta \left( \frac{K}{\sigma_y}\right)^2</math> | |||
|(5) | |||
|} | |} | ||
mit | mit | ||
{| | {| | ||
|- | |||
|<math>\sigma</math><sub>y</sub> | |<math>\sigma</math><sub>y</sub> | ||
| | |width="15px" | | ||
|Streckspannung (Streckgrenze) | |[[Streckspannung]] (Streckgrenze) | ||
|} | |} | ||
Die Geometriekonstante <math>\beta</math> ist werkstoffabhängig [4, 7–10]. | Die Geometriekonstante <math>\beta</math> ist werkstoffabhängig [4, 7–10]. | ||
''' | |||
'''Literaturhinweise''' | |||
{| | {| | ||
|-valign="top" | |-valign="top" | ||
|[1] | |[1] | ||
|Irwin, G. R.: Analysis of | |Irwin, G. R.: Analysis of Stress and Strain Near the End of a Crack Traversing a Plate. J. Appl. Mech. 24 (1957) 361 | ||
|-valign="top" | |-valign="top" | ||
|[2] | |[2] | ||
|Anderson, T. L.: Fracture Mechanics. Fundamentals and Applications. 2nd Ed., CRC Press Boca Raton (1995) ISBN 978-0849342608 | |Anderson, T. L.: Fracture Mechanics. Fundamentals and Applications. 2nd Ed., CRC Press, Boca Raton (1995) (ISBN 978-0849342608; siehe [[AMK-Büchersammlung]] unter E 8-1) | ||
|-valign="top" | |-valign="top" | ||
|[3] | |[3] | ||
|Tada, H., Paris, P.C.; Irwin, G. R.: The Stress Analysis of Cracks Handbook. 3th Ed., ASME Press, New York (2000) | |Tada, H., Paris, P. C.; Irwin, G. R.: The Stress Analysis of Cracks Handbook. 3th Ed., ASME Press, New York (2000) (ISBN 0791801535) | ||
|-valign="top" | |-valign="top" | ||
|[4] | |[4] | ||
|Blumenauer, H., Pusch, G.: Technische Bruchmechanik. Deutscher Verlag für Grundstoffindustrie, Leipzig Stuttgart (1993) ISBN 3-342- | |[[Blumenauer, Horst|Blumenauer, H.]], Pusch, G.: Technische Bruchmechanik. Deutscher Verlag für Grundstoffindustrie, Leipzig Stuttgart (1993) (ISBN 3-342-00659-5; siehe [[AMK-Büchersammlung]] unter E 29-3) | ||
|-valign="top" | |-valign="top" | ||
|[5] | |[5] | ||
|Francois, D., Pineau, A. (Eds.): From Charpy to Present Impact Testing. ESIS Publication 30, Elsevier Science Ldt. Oxford ( | |Francois, D., Pineau, A. (Eds.): From Charpy to Present Impact Testing. ESIS Publication 30, Elsevier Science Ldt. Oxford (2002) (ISBN 9780080439709) | ||
|-valign="top" | |-valign="top" | ||
|[6] | |[6] | ||
|Akay, M.: Fracture | |Akay, M.: Fracture Mechanics Properties. In: Brown, R. (Ed.): Handbook of Polymer Testing. Marcel Dekker Inc., New York (1999) (ISBN 1-85957-324-X) pp. 533–588 | ||
|-valign="top" | |-valign="top" | ||
|[7] | |[7] | ||
|Grellmann, W., Seidler, S., Hesse, W.: Prozedur zur Ermittlung des Risswiderstandsverhaltens mit dem instrumentierten Kerbschlagbiegeversuch. In: Grellmann, W., Seidler, S.: Deformation und Bruchverhalten von Kunststoffen. Springer Verlag. Berlin Heidelberg (1998) S. 75–90, (ISBN 3-540-63671-4; | |[[Grellmann,_Wolfgang|Grellmann, W.]], [[Seidler,_Sabine|Seidler, S.]], Hesse, W.: Prozedur zur Ermittlung des Risswiderstandsverhaltens mit dem instrumentierten Kerbschlagbiegeversuch. In: [https://www.researchgate.net/profile/Wolfgang-Grellmann Grellmann, W.], Seidler, S.: Deformation und Bruchverhalten von Kunststoffen. Springer Verlag. Berlin Heidelberg (1998) S. 75–90, (ISBN 3-540-63671-4; e-Book (2014): ISBN 978-3-642-58766-5; siehe [[AMK-Büchersammlung]] unter A 6) | ||
|-valign="top" | |-valign="top" | ||
|[8] | |[8] | ||
|Grellmann, W., Seidler, S. (Eds.): Deformation and Fracture Behaviour of Polymers. Springer Verlag Berlin (2001) ISBN 978-3540412472 | |[https://www.researchgate.net/profile/Wolfgang-Grellmann Grellmann, W.], Seidler, S. (Eds.): Deformation and Fracture Behaviour of Polymers. Springer Verlag, Berlin Heidelberg (2001) (ISBN 978-3540412472; siehe [[AMK-Büchersammlung]] unter A 7) | ||
|-valign="top" | |-valign="top" | ||
|[9] | |[9] | ||
|Grellmann, W., Seidler, S., Lach, R.: Geometrieunabhängige bruchmechanische Werkstoffkenngrößen – Voraussetzung für die Zähigkeitscharakterisierung von Kunststoffen. | |[https://de.wikipedia.org/wiki/Wolfgang_Grellmann Grellmann, W.], Seidler, S., [https://researchgate.net/profile/Ralf-Lach Lach, R.]: Geometrieunabhängige bruchmechanische Werkstoffkenngrößen – Voraussetzung für die Zähigkeitscharakterisierung von Kunststoffen. Material und Werkstofftechnik 32 (2001) 552–561 | ||
|-valign="top" | |-valign="top" | ||
|[10] | |[10] | ||
|Grellmann, W., Seidler, S.: Determination | |Grellmann, W., Seidler, S.: Determination of Geometry Independent Fracture Mechanics Values of Polymers. Int. J. of Fracture 68 (1994) R19–R22 | ||
|} | |} | ||
== Linear-elastische Bruchmechanik mit Kleinbereichsfließen == | == Linear-elastische Bruchmechanik mit Kleinbereichsfließen == | ||
Durch die Berücksichtigung des [[Bruchspiegel]]s a<sub>BS</sub> bei der | Durch die Berücksichtigung des [[Bruchspiegel]]s a<sub>BS</sub> bei der Beschreibung der [[Zähigkeit]] ('''Bild 5'''), wobei die [[Ausgangsrisslänge]] a um die mikroskopisch gemessene Länge des stabilen Risswachstums zu erweitern ist, wird nach | ||
{| | {| | ||
|- | |- | ||
|width="20px"| | |||
|width="500px" | <math>a_{eff}\,=\,a + a_{BS}</math> | |||
|(6) | |||
|} | |} | ||
formal der Übergang zur LEBM mit Kleinbereichsfließen vollzogen. Die experimentell überwiegend lichtmikroskopisch ermittelte Länge des [[Bruchspiegel]]s ist die Messgröße für den Radius der plastischen Zone, der in dem [[Rissmodell]] | formal der Übergang zur LEBM mit Kleinbereichsfließen vollzogen. Die experimentell überwiegend lichtmikroskopisch ermittelte Länge des [[Bruchspiegel]]s ist die [[Messgröße]] für den Radius der [[Plastische Zone|plastischen Zone]], der in dem [[Rissmodell nach IRWIN und Mc CLINTOCK]] in die Bruchmechnik eingeführt wird. Die Summe aus der [[Ausgangsrisslänge|Länge des Ausgangsrisses]] (Kerblänge) und dem [[Bruchspiegel]] wird als [[Effektive Risslänge|effektive Risslänge]] bezeichnet. Bei sehr spröden Gefügen (grobsphärolithisch) und bei hohen [[Prüfgeschwindigkeit|Beanspruchungsgeschwindigkeiten]] bzw. tiefen Temperaturen ist der [[Bruchspiegel]] vernachlässigbar klein. | ||
[[Datei:LEBM m. Kleinbereichsfließen.JPG]] | [[Datei:LEBM m. Kleinbereichsfließen.JPG]] | ||
{| | |||
{| | |- valign="top" | ||
|width="50px"|'''Bild 5''': | |||
|width="600px" |Bruchfläche eines Ethylen/Propylen Randomcopolymers mit 4 mol.-% Etyhylen (a) und schematische Darstellung der charakteristischen Bereiche (b) | |||
| | |||
|Bruchfläche eines Ethylen/Propylen Randomcopolymers mit 4 mol.-% Etyhylen (a) und schematische Darstellung der charakteristischen Bereiche (b) | |||
|} | |} | ||
== Fließbruchmechanik == | == Fließbruchmechanik == | ||
Beim makroskopisch spröden [[Bruch]] eines [[Kunststoffbauteil|Bauteils]] entsteht häufig die kritische Fehlergröße durch ein stabiles Risswachstum vorhandener Anrisse. Technisch besonders bedeutsam sind hierbei die Rissvergrößerung infolge mechanischer [[Beanspruchung]] (statisch, dynamisch, schwingend) und mediale Belastung ([[Spannungsrisskorrosion]]).<br> | |||
Falls die Ausdehnung der [[Plastische Zone|plastischen Zone]] (siehe auch „[[Effektive Risslänge]]") nicht klein im Verhältnis zu den Bauteil- oder Prüfkörperabmessungen ist, geht dem [[Bruch]] ein plastisches Fließen in größeren Werkstoffbereichen vor der [[Rissöffnung|Rissspitze]] voraus. Da dieser Fall bei den meisten Konstruktionswerkstoffen unter den üblichen Einsatzbedingungen auftritt wurde die linear-elastische Bruchmechanik zu einer Fließbruchmechanik, d. h. einer Bruchmechanik bei allgemeiner plastischer Verformung, weiterentwickelt. | |||
Die theoretische Grundlage bildet das von Wells 1961 abgeleitete [[Rissmodell nach DUGDALE|DUGDALE’sche Rissmodell]], das auf der Annahme beruht, dass der [[Bruchentstehung|Bruchvorgang]] verformungsdeterminiert ist. Dabei wird die Ausbildung einer mikrostrukturell bedingten [[Plastische Zone|plastischen Zone]] zugelassen. | |||
Neben dem auf dieser Annahme basierenden [[Crack Tip Opening Displacement-Konzept|Cack Tip Opening Displacement-(CTOD) Konzept]] sind als weitere Konzepte der Fließbruchmechanik das [[J-Integral-Konzept]] und das [[Risswiderstandskurve|Risswiderstands(R-)kurven Konzept]] etabliert. | |||
Bei elastisch-plastischen Werkstoffverhalten ist der Bruchprozess durch die Stadien Rissabstumpfung (siehe: [[Risswiderstandskurve]]), [[Rissinitiierung]], stabile [[Rissausbreitung]] und daran anschließend eventuell instabile Rissausbreitung charakterisiert. Dieser gesamte Prozess kann durch die [[Risswiderstandskurve]] (R-Kurve) der Fließbruchmechanik beschrieben werden. | |||
In den letzten Jahren sind erhebliche Fortschritte bei der Ermittlung werkstoffwissenschaftlicher [[Kennwert]]e mit den Konzepten der Fließbruchmechanik erzielt worden, wobei das spezifische Verformungs- und [[Bruchverhalten von Kunststoffbauteilen|Bruchverhalten]] der [[Kunststoffe]] besondere Berücksichtigung fand. Hierbei lieferten Methoden zur Strukturanalyse und Methoden zur Aufklärung von Verformungsmechanismen einen essentiellen Beitrag. | |||
Unter dem Aspekt der Anwendbarkeit bruchmechanischer [[Werkstoffkenngröße]]n in der Kunststoffentwicklung wird der Quantifizierung energiedissipativer Prozesse mit verallgemeinerten Integralkriterien der Bruchmechanik besondere Aufmerksamkeit gewidmet. Dazu gehört das 1986 entwickelte [[JTJ-Konzept|JT<sub>J</sub>-Konzept]] von Michel und Will, das die Quantifizierung energiedissipativer Prozesse während des stabilen Risswachstums ermöglicht. Die Eignung dieses Konzepts zur Aufstellung quantitativer Morphologie-Zähigkeits-Korrelationen wird von [[Seidler,_Sabine|Seidler]] 1996 nachgewiesen. Als morphologische Größen stehen Phasenverteilungen, -größen und -wechselwirkungen in [[Polymer|polymeren]] Mehrphasensystemen im Mittelpunkt des Interesses. | |||
Durch die Verbindung von bruchmechanischen Untersuchungsmethoden und Untersuchungen zur Morphologie werden unter Berücksichtigung der Prüftemperatur Zusammenhänge zwischen der Morphologie und dem Risseinleitungs- und -ausbreitungsverhalten verdeutlicht, die die Grundlage für quantitative Morphologie-Zähigkeits-Korrelationen bilden. | |||
==Siehe auch== | |||
*[[Bruchmechanische Prüfung]] | |||
*[[Bruch]] | |||
*[[Erkenntnisniveauebenen der Bruchmechanik]] | |||
*[[Riss]] | |||
*[[Kerb]] | |||
*[[Zähigkeit]] | |||
*[[Risszähigkeit]] | |||
'''Literaturhinweise''' | |||
* [[Blumenauer, Horst|Blumenauer, H.]], Pusch, G.: Technische Bruchmechanik. Deutscher Verlag für Grundstoffindustrie, Leipzig Stuttgart (2003), 3. Auflage, (ISBN 3-342-00659-5; siehe [[AMK-Büchersammlung]] unter E 29-3) | |||
* [[Seidler,_Sabine|Seidler, S.]]: Anwendung des Risswiderstandskonzeptes zur Ermittlung strukturbezogener bruchmechanischer Werkstoffkenngrößen bei dynamischer Beanspruchung, Habilitation (1997), Martin-Luther-Universität Halle-Wittenberg, VDI-Reihe 18: Mechanik/Bruchmechanik Nr. 231, VDI Verlag Düsseldorf (1998) (ISBN 978-3-1832-3118-8; siehe [[AMK-Büchersammlung]] unter B 2-1) | |||
* Anderson, T. L.: Fracture Mechanics; Fundamental and Applications. CRC Press, Boca Raton (2005) (ISBN 978-0849342608; siehe [[AMK-Büchersammlung]] unter E 8-2) | |||
* Krüger, L., Trubitz, P., Hentschel, S.: Bruchmechanisches Verhalten unter quasistatischer und dynamischer Beanspruchung. In: Biermann, H., Krüger, L.: Moderne Methoden der Werkstoffprüfung. Wiley-VCH Verlag GmbH, Weinheim (2014) S. 1–52; ISBN 978-3-527-33413-1 (siehe [[AMK-Büchersammlung]] unter M 35) | |||
[[Kategorie:Bruchmechanik]] | |||
[[Kategorie:Wissenschaftsdisziplinen]] | |||
Aktuelle Version vom 1. Oktober 2024, 11:27 Uhr
| Ein Service der |
|---|

|
| Polymer Service GmbH Merseburg |
| Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de |
| Unser Weiterbildungsangebot: https://www.psm-merseburg.de/weiterbildung |
| PSM bei Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg |
Bruchmechanik
Linear-elastische Bruchmechanik
Die Bruchmechanik geht davon aus, dass der Bruch eines Bauteils und damit des Werkstoffes infolge der Ausbreitung von Anrissen auftritt. Sie untersucht die Bedingungen für die Ausbreitung von Rissen (siehe Rissausbreitung) und gestattet es, zwischen der äußeren Beanspruchung, d. h. der am Bauteil oder Prüfkörper wirkenden Nennspannung, der Größe und Form der Anrisse sowie dem Widerstand des Werkstoffes gegen Rissausbreitung quantitative Zusammenhänge herzustellen.
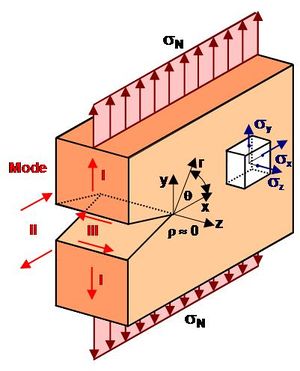
Das LEBM-Konzept beschreibt den Spannungszustand in der Nähe der Rissspitze durch den Spannungsintensitätsfaktor K (Bild 1):
| (1) |
mit
| ij | Normal- bzw. Schubspannungen | |
| r, | Polarkoordinaten mit der Rissspitze als Ursprung | |
| gij | dimensionslose Funktion. |
| Bild 1: | Koordinatensystem zur Beschreibung des Spannungszustandes an der Rissspitze |
Der von IRWIN [1] eingeführte Spannungsintensitätsfaktor ist gegeben durch
| (2) |
mit
| N | Nennspannung | |
| a | Risslänge |
Die endliche Geometrie eines jeden Bauteils und Prüfkörpers sowie die Rissgeometrie werden durch die Einführung einer Geometriefunktion f (a/W) berücksichtigt, womit Gl. 2 in der Form
| (3) |
geschrieben werden kann. Die Funktionen f (a/W) sind für eine Vielzahl von Bruchmechanikprüfkörpern berechnet worden [2, 3]. Die Bilder 2 und 3 enthalten die Abmessungen von bevorzugt für Kunststoffe angewandte Prüfkörper. Für einen unendlich ausgedehnten Prüfkörper und den Grenzfall eines Risses mit einem Kerbradius ~ 0 ist die Geometriefunktion f (a/W) = 1.
Der Spannungsintensitätsfaktor erreicht zu Beginn der instabilen Rissausbreitung einen kritischen Wert KIc, der als Bruch- oder Risszähigkeit bezeichnet wird und die Dimension MPa mm1/2 erhält. Der Index I weist auf die Mode I-Belastung hin, bei der
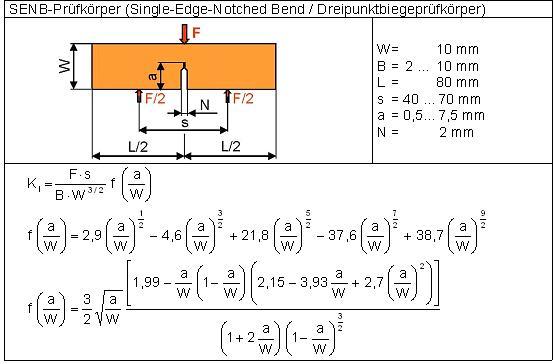
| Bild 2: | Prüfkörperform SENB mit Abmessungen, den dazugehörigen Bestimmungsgleichungen zur Berechnung der Bruchzähigkeiten und der Geometriefunktionen. |
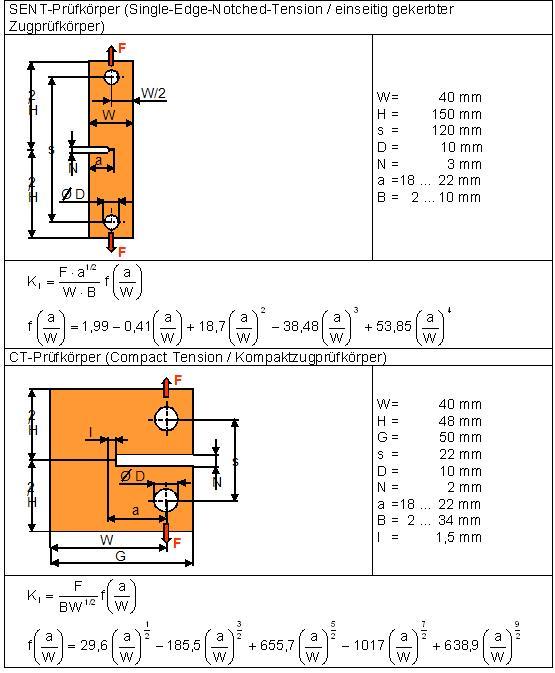
| Bild 3: | Prüfkörperformen SENT und CT mit ihren Abmessungen, den dazugehörigen Bestimmungsgleichungen zur Berechnung der Bruchzähigkeiten und den Geometriefunktionen |
die Belastung senkrecht zur Rissfläche erfolgt. Für diesen technisch wichtigsten Fall einer Beanspruchung lautet das Bruchsicherheitskriterium
| (4) |
wonach die Bruchsicherheit eines Bauteils gewährleistet ist, solange der kritische Wert nicht überschritten wird.
Neben der einfachen Rissöffnung nach Mode I sind in Bild 1 auch die Rissöffnungsmoden II und III enthalten, die bei Scher- oder Torsionsbeanspruchungen auftreten.
In Abhängigkeit von der Prüfkörpergeometrie bilden sich vor der Rissspitze unterschiedliche mehrachsige Spannungszustände aus.
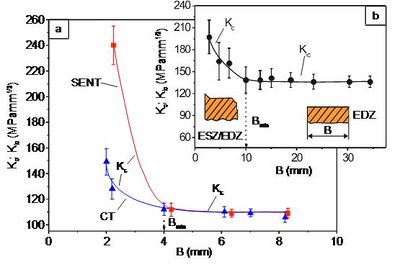
Das Bild 4 zeigt am Beispiel von nachchlorierten PVC (Kurzzeichen: PVCC) und Polypropylen (Kurzzeichen: PP) den Einfluss der Prüfkörperdicke auf das Bruchverhalten, wobei resultierend aus dem Übergang vom ebenen Spannungszustand (ESZ) in den ebenen Dehnungszustand (EDZ) makroskopisch ein Anwachsen des Normalspannungsbruches beobachtet wird.
Für den Fall, dass an der Rissspitze EDZ vorliegt, wird die Bruchzähigkeit von der Prüfkörpergeometrie unabhängig. Sie gibt den Einfluss der Werkstoffstruktur, der Geschwindigkeit und der Umgebungstemperatur auf die Zähigkeit wieder.
| Bild 4: | Abhängigkeit der Bruchzähigkeit Kc, KIc bei Raumtemperatur von der Prüfkörperdicke bei quasistatischer Beanspruchung für PVCC mit KIc = 110 MPamm1/2 (a) und für PP mit KIc = 139 MPamm1/2 (b) bei einer Traversengeschwindigkeit von vT = 8,3 • 10-4 ms-1 |
Bei linear-elastischer Betrachtungsweise erfolgt die Abschätzung der Geometriegrößen B, a und der Ligamentausdehnung (W – a) über die empirisch ermittelte Beziehung [2, 4–6]
| (5) |
mit
| y | Streckspannung (Streckgrenze) |
Die Geometriekonstante ist werkstoffabhängig [4, 7–10].
Literaturhinweise
| [1] | Irwin, G. R.: Analysis of Stress and Strain Near the End of a Crack Traversing a Plate. J. Appl. Mech. 24 (1957) 361 |
| [2] | Anderson, T. L.: Fracture Mechanics. Fundamentals and Applications. 2nd Ed., CRC Press, Boca Raton (1995) (ISBN 978-0849342608; siehe AMK-Büchersammlung unter E 8-1) |
| [3] | Tada, H., Paris, P. C.; Irwin, G. R.: The Stress Analysis of Cracks Handbook. 3th Ed., ASME Press, New York (2000) (ISBN 0791801535) |
| [4] | Blumenauer, H., Pusch, G.: Technische Bruchmechanik. Deutscher Verlag für Grundstoffindustrie, Leipzig Stuttgart (1993) (ISBN 3-342-00659-5; siehe AMK-Büchersammlung unter E 29-3) |
| [5] | Francois, D., Pineau, A. (Eds.): From Charpy to Present Impact Testing. ESIS Publication 30, Elsevier Science Ldt. Oxford (2002) (ISBN 9780080439709) |
| [6] | Akay, M.: Fracture Mechanics Properties. In: Brown, R. (Ed.): Handbook of Polymer Testing. Marcel Dekker Inc., New York (1999) (ISBN 1-85957-324-X) pp. 533–588 |
| [7] | Grellmann, W., Seidler, S., Hesse, W.: Prozedur zur Ermittlung des Risswiderstandsverhaltens mit dem instrumentierten Kerbschlagbiegeversuch. In: Grellmann, W., Seidler, S.: Deformation und Bruchverhalten von Kunststoffen. Springer Verlag. Berlin Heidelberg (1998) S. 75–90, (ISBN 3-540-63671-4; e-Book (2014): ISBN 978-3-642-58766-5; siehe AMK-Büchersammlung unter A 6) |
| [8] | Grellmann, W., Seidler, S. (Eds.): Deformation and Fracture Behaviour of Polymers. Springer Verlag, Berlin Heidelberg (2001) (ISBN 978-3540412472; siehe AMK-Büchersammlung unter A 7) |
| [9] | Grellmann, W., Seidler, S., Lach, R.: Geometrieunabhängige bruchmechanische Werkstoffkenngrößen – Voraussetzung für die Zähigkeitscharakterisierung von Kunststoffen. Material und Werkstofftechnik 32 (2001) 552–561 |
| [10] | Grellmann, W., Seidler, S.: Determination of Geometry Independent Fracture Mechanics Values of Polymers. Int. J. of Fracture 68 (1994) R19–R22 |
Linear-elastische Bruchmechanik mit Kleinbereichsfließen
Durch die Berücksichtigung des Bruchspiegels aBS bei der Beschreibung der Zähigkeit (Bild 5), wobei die Ausgangsrisslänge a um die mikroskopisch gemessene Länge des stabilen Risswachstums zu erweitern ist, wird nach
| (6) |
formal der Übergang zur LEBM mit Kleinbereichsfließen vollzogen. Die experimentell überwiegend lichtmikroskopisch ermittelte Länge des Bruchspiegels ist die Messgröße für den Radius der plastischen Zone, der in dem Rissmodell nach IRWIN und Mc CLINTOCK in die Bruchmechnik eingeführt wird. Die Summe aus der Länge des Ausgangsrisses (Kerblänge) und dem Bruchspiegel wird als effektive Risslänge bezeichnet. Bei sehr spröden Gefügen (grobsphärolithisch) und bei hohen Beanspruchungsgeschwindigkeiten bzw. tiefen Temperaturen ist der Bruchspiegel vernachlässigbar klein.
| Bild 5: | Bruchfläche eines Ethylen/Propylen Randomcopolymers mit 4 mol.-% Etyhylen (a) und schematische Darstellung der charakteristischen Bereiche (b) |
Fließbruchmechanik
Beim makroskopisch spröden Bruch eines Bauteils entsteht häufig die kritische Fehlergröße durch ein stabiles Risswachstum vorhandener Anrisse. Technisch besonders bedeutsam sind hierbei die Rissvergrößerung infolge mechanischer Beanspruchung (statisch, dynamisch, schwingend) und mediale Belastung (Spannungsrisskorrosion).
Falls die Ausdehnung der plastischen Zone (siehe auch „Effektive Risslänge") nicht klein im Verhältnis zu den Bauteil- oder Prüfkörperabmessungen ist, geht dem Bruch ein plastisches Fließen in größeren Werkstoffbereichen vor der Rissspitze voraus. Da dieser Fall bei den meisten Konstruktionswerkstoffen unter den üblichen Einsatzbedingungen auftritt wurde die linear-elastische Bruchmechanik zu einer Fließbruchmechanik, d. h. einer Bruchmechanik bei allgemeiner plastischer Verformung, weiterentwickelt.
Die theoretische Grundlage bildet das von Wells 1961 abgeleitete DUGDALE’sche Rissmodell, das auf der Annahme beruht, dass der Bruchvorgang verformungsdeterminiert ist. Dabei wird die Ausbildung einer mikrostrukturell bedingten plastischen Zone zugelassen. Neben dem auf dieser Annahme basierenden Cack Tip Opening Displacement-(CTOD) Konzept sind als weitere Konzepte der Fließbruchmechanik das J-Integral-Konzept und das Risswiderstands(R-)kurven Konzept etabliert.
Bei elastisch-plastischen Werkstoffverhalten ist der Bruchprozess durch die Stadien Rissabstumpfung (siehe: Risswiderstandskurve), Rissinitiierung, stabile Rissausbreitung und daran anschließend eventuell instabile Rissausbreitung charakterisiert. Dieser gesamte Prozess kann durch die Risswiderstandskurve (R-Kurve) der Fließbruchmechanik beschrieben werden.
In den letzten Jahren sind erhebliche Fortschritte bei der Ermittlung werkstoffwissenschaftlicher Kennwerte mit den Konzepten der Fließbruchmechanik erzielt worden, wobei das spezifische Verformungs- und Bruchverhalten der Kunststoffe besondere Berücksichtigung fand. Hierbei lieferten Methoden zur Strukturanalyse und Methoden zur Aufklärung von Verformungsmechanismen einen essentiellen Beitrag.
Unter dem Aspekt der Anwendbarkeit bruchmechanischer Werkstoffkenngrößen in der Kunststoffentwicklung wird der Quantifizierung energiedissipativer Prozesse mit verallgemeinerten Integralkriterien der Bruchmechanik besondere Aufmerksamkeit gewidmet. Dazu gehört das 1986 entwickelte JTJ-Konzept von Michel und Will, das die Quantifizierung energiedissipativer Prozesse während des stabilen Risswachstums ermöglicht. Die Eignung dieses Konzepts zur Aufstellung quantitativer Morphologie-Zähigkeits-Korrelationen wird von Seidler 1996 nachgewiesen. Als morphologische Größen stehen Phasenverteilungen, -größen und -wechselwirkungen in polymeren Mehrphasensystemen im Mittelpunkt des Interesses.
Durch die Verbindung von bruchmechanischen Untersuchungsmethoden und Untersuchungen zur Morphologie werden unter Berücksichtigung der Prüftemperatur Zusammenhänge zwischen der Morphologie und dem Risseinleitungs- und -ausbreitungsverhalten verdeutlicht, die die Grundlage für quantitative Morphologie-Zähigkeits-Korrelationen bilden.
Siehe auch
- Bruchmechanische Prüfung
- Bruch
- Erkenntnisniveauebenen der Bruchmechanik
- Riss
- Kerb
- Zähigkeit
- Risszähigkeit
Literaturhinweise
- Blumenauer, H., Pusch, G.: Technische Bruchmechanik. Deutscher Verlag für Grundstoffindustrie, Leipzig Stuttgart (2003), 3. Auflage, (ISBN 3-342-00659-5; siehe AMK-Büchersammlung unter E 29-3)
- Seidler, S.: Anwendung des Risswiderstandskonzeptes zur Ermittlung strukturbezogener bruchmechanischer Werkstoffkenngrößen bei dynamischer Beanspruchung, Habilitation (1997), Martin-Luther-Universität Halle-Wittenberg, VDI-Reihe 18: Mechanik/Bruchmechanik Nr. 231, VDI Verlag Düsseldorf (1998) (ISBN 978-3-1832-3118-8; siehe AMK-Büchersammlung unter B 2-1)
- Anderson, T. L.: Fracture Mechanics; Fundamental and Applications. CRC Press, Boca Raton (2005) (ISBN 978-0849342608; siehe AMK-Büchersammlung unter E 8-2)
- Krüger, L., Trubitz, P., Hentschel, S.: Bruchmechanisches Verhalten unter quasistatischer und dynamischer Beanspruchung. In: Biermann, H., Krüger, L.: Moderne Methoden der Werkstoffprüfung. Wiley-VCH Verlag GmbH, Weinheim (2014) S. 1–52; ISBN 978-3-527-33413-1 (siehe AMK-Büchersammlung unter M 35)