IKBV Einfluss Hammergeschwindigkeit: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| (2 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 38: | Zeile 38: | ||
Während sich die Bruchkräfte für v<sub>H</sub> > 1,5 … 2 ms<sup>-1</sup> nicht mehr wesentlich ändern (vgl. '''Bild 2''') wird in [1] nachgewiesen, dass die Prüfkörperdurchbiegung mit steigender Pendelhammergeschwindigkeit erwartungsgemäß sinkt und damit als Indikator für die mit steigender Geschwindigkeit zunehmende Versprödung angesehen werden kann [5]. | Während sich die Bruchkräfte für v<sub>H</sub> > 1,5 … 2 ms<sup>-1</sup> nicht mehr wesentlich ändern (vgl. '''Bild 2''') wird in [1] nachgewiesen, dass die Prüfkörperdurchbiegung mit steigender Pendelhammergeschwindigkeit erwartungsgemäß sinkt und damit als Indikator für die mit steigender Geschwindigkeit zunehmende Versprödung angesehen werden kann [5]. | ||
==Siehe auch== | |||
*[[Instrumentierter Kerbschlagbiegeversuch]] | |||
*[[IKBV Experimentelle Bedingungen]] | |||
*[[Schlagbeanspruchung Pendelschlagwerk]] | |||
| Zeile 44: | Zeile 49: | ||
|-valign="top" | |-valign="top" | ||
|[1] | |[1] | ||
|[[Grellmann,_Wolfgang|Grellmann, W.]]: Beurteilung der Zähigkeitseigenschaften von Polymerwerkstoffen durch bruchmechanische Kennwerte. Habilitation (1986), Technische Hochschule Merseburg, Wiss. Zeitschrift TH Merseburg 28 (1986), H. 6, S. 787–788 ([ | |[[Grellmann,_Wolfgang|Grellmann, W.]]: Beurteilung der Zähigkeitseigenschaften von Polymerwerkstoffen durch bruchmechanische Kennwerte. Habilitation (1986), [https://de.wikipedia.org/wiki/Technische_Hochschule_Leuna-Merseburg Technische Hochschule Merseburg], Wiss. Zeitschrift TH Merseburg 28 (1986), H. 6, S. 787–788 ([https://www.polymerservice-merseburg.de/fileadmin/inhalte/psm/veroeffentlichungen/Habil_Grellmann_Inhaltsverzeichnis.pdf Inhaltsverzeichnis], [https://www.polymerservice-merseburg.de/fileadmin/inhalte/psm/veroeffentlichungen/Habil_Grellmann_Kurzfassung.pdf Kurzfassung]) | ||
|-valign="top" | |-valign="top" | ||
|[2] | |[2] | ||
| Zeile 56: | Zeile 61: | ||
|-valign="top" | |-valign="top" | ||
|[5] | |[5] | ||
|Grellmann, W., [[Seidler,_Sabine|Seidler, S.]] (Hrsg.): Kunststoffprüfung. Carl Hanser Verlag, München ( | |[https://www.researchgate.net/profile/Wolfgang-Grellmann Grellmann, W.], [[Seidler,_Sabine|Seidler, S.]] (Hrsg.): Kunststoffprüfung. Carl Hanser Verlag, München (2024) 4. Auflage (ISBN 978-3-446-44718-9; E-Book: ISBN 978-3-446-48105-3; siehe [[AMK-Büchersammlung]] unter A 23) | ||
|} | |} | ||
[[Kategorie:Bruchmechanik]][[Kategorie:Instrumentierter Kerbschlagbiegeversuch]] | [[Kategorie:Bruchmechanik]][[Kategorie:Instrumentierter Kerbschlagbiegeversuch]] | ||
Aktuelle Version vom 22. Oktober 2024, 12:28 Uhr
| Ein Service der |
|---|

|
| Polymer Service GmbH Merseburg |
| Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de |
| Unser Weiterbildungsangebot: https://www.psm-merseburg.de/weiterbildung |
| PSM bei Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg |
IKBV Einfluss Hammergeschwindigkeit
IKBV Verhältnis der Bruchkraft zur Amplitude der Trägheitskraft
Für die bruchmechanische Auswertung von im instrumentierten Kerbschlagbiegeversuch registrierten Schlagkraft (F)-Durchbiegungs (f)-Diagrammen nach den Kriterien der Linear-elastischen Bruchmechanik (LEBM) und der Fließbruchmechanik (siehe J-Integral-Konzept und Crack-Tip-Opening- Displacement-Konzept besteht die Bedingung, dass die Bruchkraft Fmax beim instabilen Rissfortschritt immer deutlich größer sein muss als die Amplitude der Trägheitskraft F1 (siehe IKBV Experimentelle Bedingungen) [1].
Anwendung der Low-Blow-Methode
Eine bewährte Technik ist die Verringerung der Pendelhammergeschwindigkeit vH (Low-Blow-Technik [2‒4]). Hierfür ist es lediglich notwendig, die Fallhöhe herabzusetzen, wodurch gleichzeitig der Arbeitsinhalt des Pendels gesenkt wird (siehe auch: Schlagbeanspruchung Pendelschlagwerk).
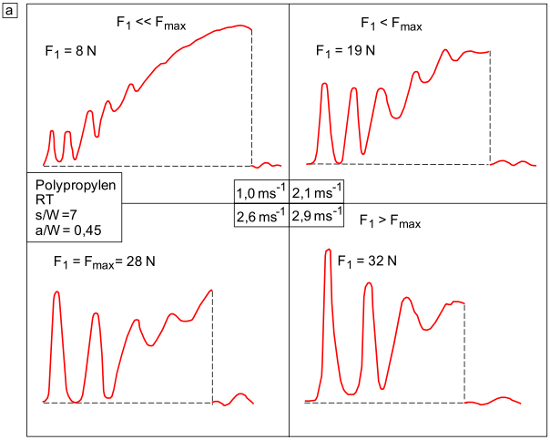
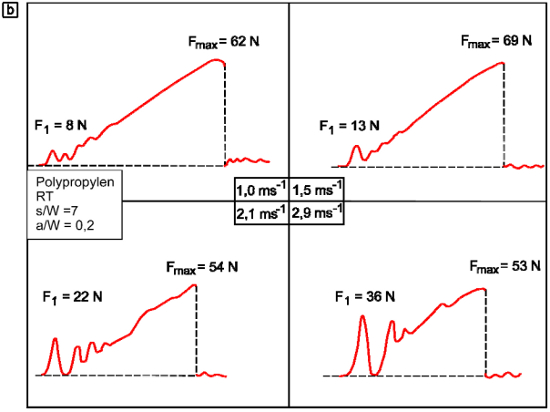
Die Auswirkungen einer reduzierten Pendelhammergeschwindigkeit wird im Bild 1 am Beispiel des Polypropylen (Kurzzeichen: PP) gezeigt, wobei eine deutliche Änderung des Werkstoffverhaltens zu erkennen ist.
| Bild 1: | Einfluss einer reduzierten Pendelhammergeschwindigkeit auf das Werkstoffverhalten von Polypropylen (Kurzzeichen: PP) für s/W = 7, RT und a/W = 0,45 (a) und a/W = 0,2 (b) |
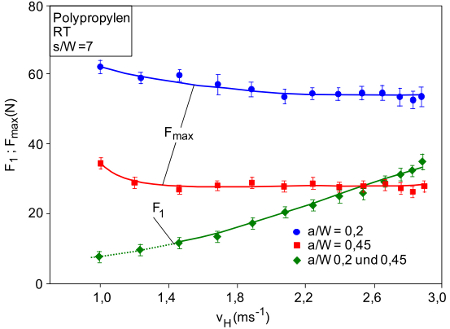
Aus Bild 1 wird ersichtlich, dass bei einer Pendelhammergeschwindigkeit vH = 2,9 ms-1 und a/W = 0,45 die maximale Schlagkraft deutlich kleiner als die Amplitude der Trägheitskraft F1 ist und somit bei nahezu mittig gekerbten Prüfkörper keine bruchmechanische Auswertung nach Konzepten der Bruchmechanik möglich ist. Die aus den Teilbildern ersichtliche Zunahme der Amplitude der Trägheitskraft ist im Verhältnis zur Abnahme der Bruchkraft Fmax für a/W = 0,2 und a/W = 0,45 in Bild 2 dargestellt.
| Bild 2: | Abhängigkeit der maximalen Schlagkraft Fmax und der Trägheitskraft F1 von der Pendelhammergeschwindigkeit für Polypropylen (Kurzzeichen: PP) bei a/W = 0,2 und a/W = 0,45 |
Während bei a/W = 0,2 die Trägheitskräfte (vgl. Bild 1a) auch bei maximal möglichen Hammergeschwindigkeiten von 2,9 ms-1 noch kleiner als die Bruchkräfte sind, ist diese Bedingung für a/W = 0,45 nicht mehr erfüllt. Für dieses a/W-Verhältnis sind F1 und Fmax bei 2,6 ms-1 identisch und bei vH > 2,6 ms-1 ist F1 > Fmax, so dass die Beziehung Fmax > F1 nicht erfüllt ist und keine exakte Angabe bruchmechanischer Kennwerte möglich wird. Die Trägheitskräfte liegen im Bereich zwischen 8 N ≤ F1 ≤ 36 N und sind nahezu unabhängig vom a/W-Verhältnis. Zwischen der Amplitude der Trägheitskräfte kann der zu erwartende lineare Zusammenhang mit der Pendelhammergeschwindigkeit für beide a/W-Verhältnisse bestätigt werden [1]. Für vH > 1,5 ms-1 wird als werkstoffspezifischer Anstieg für Polypropylen (Kurzzeichen: PP) ein Wert von 15 Ns/m ermittelt und für vH < 1,5 ms-1 ist experimentell ein anderer Anstieg beobachtet worden, der aus der Bedingung F1 → 0 für vH → 0 sinnvoll ist. Der Unterschied in der Bruchkraft Fmax für a/W = 0,2 und a/W = 0,45 resultiert aus der Veränderung des Restquerschnittes (Ligament x Prüfkörperdicke).
Bruchmechanisch auswertbare Registrierdiagramme
Hieraus wird ersichtlich, dass auswertbare, d. h. den Kontrollbedingungen Fmax > F1 und tB > 2,3…3τ (siehe IKBV Experimentelle Bedingungen) genügende F-f-Diagramme für die Bestimmung bruchmechanischer Kennwerte bei hohen Hammergeschwindigkeiten nur für kleine a/W-Verhältnisse zu erwarten sind. Mit abnehmender Geschwindigkeit wird der Zusammenhang zwischen Kraft und Durchbiegung immer nichtlinearer. Auf Grund der mit abnehmender Prüftemperatur steigenden Werkstoffversprödung, die mit einer Verringerung der Bruchzeiten tB verbunden ist, kann die Erfüllung der Kontrollbedingung Fmax > F1 bei tiefen Temperaturen und hohem a/W-Verhältnis nicht realisiert werden. Die Kontrolle der Energiebilanz, wonach die von der Probe verbrauchte Schlagarbeit kleiner als ein Drittel der Gesamtenergie des Pendelschlagwerkes sein muss, ergab, dass diese Bedingungen auch bei einer Hammergeschwindigkeit von 1 ms-1 (~ 40° Hammerfallwinkel) hinreichend erfüllt ist [1].
Während sich die Bruchkräfte für vH > 1,5 … 2 ms-1 nicht mehr wesentlich ändern (vgl. Bild 2) wird in [1] nachgewiesen, dass die Prüfkörperdurchbiegung mit steigender Pendelhammergeschwindigkeit erwartungsgemäß sinkt und damit als Indikator für die mit steigender Geschwindigkeit zunehmende Versprödung angesehen werden kann [5].
Siehe auch
- Instrumentierter Kerbschlagbiegeversuch
- IKBV Experimentelle Bedingungen
- Schlagbeanspruchung Pendelschlagwerk
Literaturhinweise
| [1] | Grellmann, W.: Beurteilung der Zähigkeitseigenschaften von Polymerwerkstoffen durch bruchmechanische Kennwerte. Habilitation (1986), Technische Hochschule Merseburg, Wiss. Zeitschrift TH Merseburg 28 (1986), H. 6, S. 787–788 (Inhaltsverzeichnis, Kurzfassung) |
| [2] | Retting, W.: Materialprüfung 8 (1966) 2, S. 55 |
| [3] | Ortmann, R.; Man, J.: Wiss. Zeitschrift TH Magdeburg 24 (1980) 1, S. 101 |
| [4] | Holzmann, M., Man, J.: Dynamika Lomova Houzevnatost (Dynamische Bruchzähigkeit), Zvaranie (1977) 5‒9 S. 1‒43 |
| [5] | Grellmann, W., Seidler, S. (Hrsg.): Kunststoffprüfung. Carl Hanser Verlag, München (2024) 4. Auflage (ISBN 978-3-446-44718-9; E-Book: ISBN 978-3-446-48105-3; siehe AMK-Büchersammlung unter A 23) |