Biegebeanspruchung: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| (13 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Language_sel|LANG=eng|ARTIKEL=Bend Loading}} | |||
{{PSM_Infobox}} | |||
<span style="font-size:1.2em;font-weight:bold;">Biegebeanspruchung</span> | <span style="font-size:1.2em;font-weight:bold;">Biegebeanspruchung</span> | ||
__FORCETOC__ | |||
==Allgemeines== | |||
Die Biegebeanspruchung entspricht einer der häufigsten, in der Praxis auftretenden [[Beanspruchung]]sarten und besitzt deshalb eine große Bedeutung für die [[Kennwert]]ermittlung an [[Kunststoffe]]n und [[Faserverstärkte Kunststoffe|Faserverbundwerkstoffen]]. Die Belastungsart wird speziell für folgende Prüfverfahren verwendet: | |||
* [[Biegeversuch]] zur Charakterisierung von [[Thermoplaste|thermo]]- und [[Duroplaste|duroplastischen]] [[Formmasse]]n und [[Teilchengefüllte Kunststoffe|gefüllten]] sowie [[Faserverstärkte Kunststoffe|verstärkten]] [[Prüfung von Verbundwerkstoffen|Verbundwerkstoffen]], | |||
* [[Biegeversuch]] zur Charakterisierung von thermo- und duroplastischen | |||
* mechanisch-thermische Biegebeanspruchung zur Bestimmung der [[Wärmeformbeständigkeit]] im HDT-Test sowie | * mechanisch-thermische Biegebeanspruchung zur Bestimmung der [[Wärmeformbeständigkeit]] im HDT-Test sowie | ||
* medial-mechanische Biegebeanspruchung zur Ermittlung der [[Spannungsrissbeständigkeit]] | * medial-mechanische Biegebeanspruchung zur Ermittlung der [[Spannungsrissbeständigkeit]] | ||
==Quasistatischer Biegeversuch== | |||
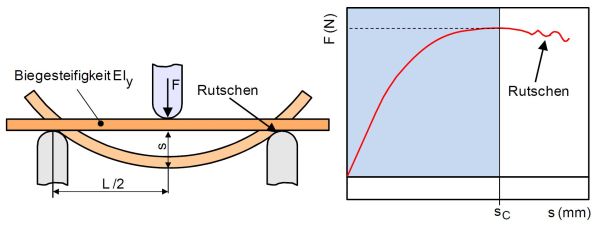
Der [[Quasistatische Prüfverfahren|quasistatische]] [[Biegeversuch]] sollte insbesondere zur Prüfung spröder Werkstoffe eingesetzt werden, die im [[Zugversuch]] auf Grund ihres Versagensverhaltens messtechnische Probleme bereiten. In der prüftechnischen Praxis wird dieser Versuch jedoch auch für duktile [[Kunststoffe]] genutzt, die bei Biegebeanspruchung nicht brechen, weshalb der Versuch bei Erreichen eines Grenzzustandes (konventionelle Durchbiegung s = 1,5 h mit h = Prüfkörperdicke) abgebrochen wird. Damit soll der Einfluss des Rutschens (stick-slip) auf den [[Auflagerabstand|Widerlagern]] bei großen Durchbiegungen vermieden werden ('''Bild 1'''). | |||
[[Datei:biegebeanspruchung1.jpg]] | |||
{| | |||
|- valign="top" | |||
|width="50px"|'''Bild 1''': | |||
|width="600px" |Rutschen des Prüfkörpers auf den Widerlager bei großen Durchbiegungen | |||
|} | |||
Wie bei der [[zugversuch|Zug-]] oder [[Druckversuch|Druckbeanspruchung]] sind auch bei der Biegebelastung die unterschiedlichen [[Deformation|Deformationsanteile]], die zeitlich und lastabhängig wirksam werden, bei der Bewertung der Messergebnisse zu berücksichtigen. In Abhängigkeit vom Typ des [[Kunststoffe]]s treten ebenfalls [[Deformation#Elastische Deformation|linear-elastische]], [[linear-viskoelastisches Verhalten|linear-viskoelastische]], [[Elastizität|nichtlinear-viskoelastische]] und [[Deformation#Plastische Deformation|plastische]] Verformungsanteile auf, wobei das Verhältnis der Verformungsanteile in Bezug auf die Gesamtverformung vom jeweiligen Kunststoff sowie den Beanspruchungsbedingungen (Temperatur und [[Prüfgeschwindigkeit]]) abhängt. Demzufolge sind die im [[Biegeversuch]] ermittelten [[Werkstoffkennwert|Kennwerte]] eine Funktion der Verformung, der [[Dehnrate Grundlagen|Dehngeschwindigkeit]], der Belastung oder Spannung, der Temperatur und des inneren Zustandes des [[Prüfkörper]]s. | |||
==Bestimmung des Biegemomentenverlaufs== | |||
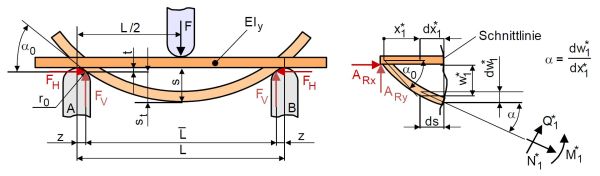
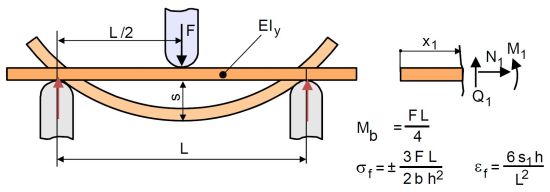
Für die Auswertung des Biegeverhaltens und die Berechnung der Biegespannung sowie der zugehörigen [[Randfaserdehnung]]en wird die elastische Linie bei Kenntnis des Biegemomentenverlaufs (Dreipunkt- oder Vierpunktbiegelinie) herangezogen. Die Biegelinie des verformten [[Prüfkörper]]s ergibt sich nach Gl. (1) und '''Bild 2''' wie folgt: | |||
{| | |||
|- | |||
|width="20px"| | |||
|width="500px" | <math>\frac{s^{\prime \prime}(x)}{[1+s^{\prime 2}(x)]^{\frac {3}{2}}}=-\frac{M_{b}(x)}{E\ I_{y}}</math> | |||
|(1) | |||
|} | |||
[[Datei:biegebeanspruchung2.jpg]] | |||
{| | |||
|- valign="top" | |||
|width="50px"|'''Bild 2''': | |||
|width="600px" |Biegelinie bei Dreipunktbiegung am deformierten Prüfkörper (Theorie 2. Ordnung) | |||
|} | |||
Da diese Differentialgleichung als auch die zugehörigen Randbedingungen von der Neigung der elastischen Linie abhängen, kann diese Gleichung nur auf numerischen Weg gelöst werden. Für eine ingenieurtechnisch handhabbare Lösung wurde deshalb die Nutzung der Biegelinie am unverformten [[Prüfkörper]] vereinbart. Damit wird die Neigung der Biegeline mit ds/dx ≈ 0 vernachlässigbar und es entsteht die vereinfachte Biegelinie nach Gl. (2) und '''Bild 3''': | |||
{| | |||
|- | |||
|width="20px"| | |||
|width="500px" | <math>s^{\prime \prime}(x)=-\frac{M_{b}(x)}{E\ I_{y}}</math> | |||
|(2) | |||
|} | |||
[[Datei:biegebeanspruchung3.jpg]] | |||
{| | |||
|- valign="top" | |||
|width="50px"|'''Bild 3''': | |||
|width="600px" |Biegelinie des undeformierten Prüfkörper (Theorie 1. Ordnung) | |||
|} | |||
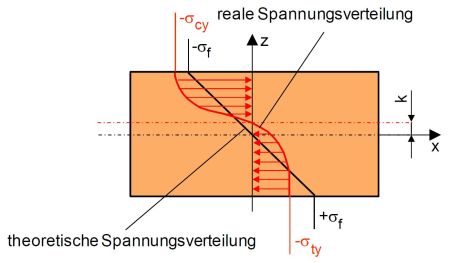
Die Lösung dieser Differentialgleichung mit der Biegespannung σ<sub>f</sub> und der Randfaserdehnung ε<sub>f</sub> ist jedoch nur für kleine Durchbiegungen (s << h) gültig, weshalb in der prüftechnischen Praxis mit Durchbiegungen von bis zu 6 mm (s = 1,5 h, h = 4 mm) oftmals interpretative Probleme bei duktilen [[Kunststoffe]]n entstehen. Die Anwendung dieser Auswertegleichungen setzt außerdem eine symmetrische Spannungs- und Dehnungsverteilung über den Querschnitt voraus, so dass die Nulllinie der Spannung oder Dehnung identisch mit der neutralen Faser des Biegebalkens ist. Infolge des teilweise sehr unterschiedlichen Zug- und Druckverhaltens der Kunststoffe (siehe PS) mit differierenden Fließspannungen σ<sub>ty</sub> und σ<sub>cy</sub> kann es deshalb zu einer Verschiebung k der neutralen Faser ('''Bild 4''') kommen, wodurch die Auswertegleichungen des [[Biegeversuch]]s eigentlich nicht mehr anwendbar sind. | |||
[[Datei:biegebeanspruchung4.jpg]] | |||
{| | |||
|- valign="top" | |||
|width="50px"|'''Bild 4''': | |||
|width="600px" |Verschiebung der neutralen Faser bei unterschiedlichem Zug- und Druckverhalten | |||
|} | |||
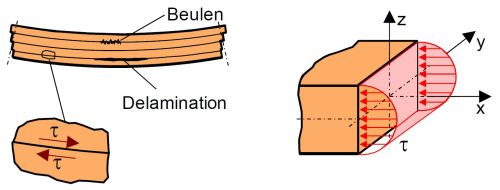
Neben diesen Normalspannungen entstehen insbesondere bei dicken Prüfkörpern oder sehr geringen [[Auflagerabstand|Stützweiten]] parabolisch über den Querschnitt verteilte [[Biegeversuch Schubspannung|Schubspannungen]] ('''Bild 5'''), die speziell bei Laminaten auf der Zugseite Delaminationen zwischen den Schichten verursachen können und zu fehlerbehafteten Kennwerten führen. Aus diesem Grund sollte das Stützweiten/Höhen-Verhältnis bei isotropen und homogenen [[Kunststoffe]]n L = (16 ± 1) h betragen und bei Laminaten sollte ein Verhältnis von L = (20 – 25 ± 1) h eingehalten werden. | |||
[[Datei:biegebeanspruchung5.jpg]] | |||
{| | |||
|- valign="top" | |||
|width="50px"|'''Bild 5''': | |||
|width="600px" |Auswirkungen von Schubspannungen im Querschnitt | |||
|} | |||
Eine umfassende Literaturanalyse zu den mechanischen Kennwerten ε<sub>f</sub>, σ<sub>fM</sub> und σ<sub>fc</sub> bei Biegebeanspruchung für zahlreiche Kunststoffe ist in [3] enthalten. | |||
==Siehe auch== | |||
*[[Biegeversuch]] | |||
*[[Biegemodul]] | |||
*[[Dynamisch-Mechanische Analyse (DMA) – Biegebeanspruchung]] | |||
*[[Biegestreifenverfahren]] | |||
*[[Biegeversuch und Schallemissionsanalyse]] | |||
*[[Randfaserdehnung]] | |||
'''Literaturhinweise''' | |||
{| | |||
|-valign="top" | |||
|[1] | |||
|[[Bierögel,_Christian|Bierögel, C.]]: Biegeversuch an Kunststoffen. In: [[Grellmann,_Wolfgang|Grellmann, W.]], [[Seidler,_Sabine|Seidler, S.]] (Hrsg.): Kunststoffprüfung. Carl Hanser Verlag, München (2024) 4. Auflage, S. 141–151 (ISBN 978-3-446-44718-9; E-Book: ISBN 978-3-446-48105-3; siehe [[AMK-Büchersammlung]] unter A 23) | |||
|-valign="top" | |||
|[2] | |||
|Szabó, I.: Einführung in die Technische Mechanik. Springer Verlag, Berlin, Heidelberg (1984) 8. Auflage, (ISBN 3-540-13293-7; siehe [[AMK-Büchersammlung]] unter T 15) | |||
|-valign="top" | |||
|[3] | |||
|Bierögel, C., [https://www.researchgate.net/profile/Wolfgang-Grellmann Grellmann, W.]: Bend Loading. In: Grellmann, W., Seidler, S.: Mechanical and Thermomechanical Properties of Polymers. Landolt-Börnstein. Volume VIII/6A3, Springer Verlag, Berlin (2014) S. 164–191, (ISBN 978-3-642-55165-9; siehe [[AMK-Büchersammlung]] unter A 16) | |||
|} | |||
[[Kategorie:Biegeversuch]] | |||
Aktuelle Version vom 8. Januar 2026, 09:20 Uhr
| Ein Service der |
|---|

|
| Polymer Service GmbH Merseburg |
| Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de |
| Unser Weiterbildungsangebot: https://www.psm-merseburg.de/weiterbildung |
| PSM bei Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg |
Biegebeanspruchung
Allgemeines
Die Biegebeanspruchung entspricht einer der häufigsten, in der Praxis auftretenden Beanspruchungsarten und besitzt deshalb eine große Bedeutung für die Kennwertermittlung an Kunststoffen und Faserverbundwerkstoffen. Die Belastungsart wird speziell für folgende Prüfverfahren verwendet:
- Biegeversuch zur Charakterisierung von thermo- und duroplastischen Formmassen und gefüllten sowie verstärkten Verbundwerkstoffen,
- mechanisch-thermische Biegebeanspruchung zur Bestimmung der Wärmeformbeständigkeit im HDT-Test sowie
- medial-mechanische Biegebeanspruchung zur Ermittlung der Spannungsrissbeständigkeit
Quasistatischer Biegeversuch
Der quasistatische Biegeversuch sollte insbesondere zur Prüfung spröder Werkstoffe eingesetzt werden, die im Zugversuch auf Grund ihres Versagensverhaltens messtechnische Probleme bereiten. In der prüftechnischen Praxis wird dieser Versuch jedoch auch für duktile Kunststoffe genutzt, die bei Biegebeanspruchung nicht brechen, weshalb der Versuch bei Erreichen eines Grenzzustandes (konventionelle Durchbiegung s = 1,5 h mit h = Prüfkörperdicke) abgebrochen wird. Damit soll der Einfluss des Rutschens (stick-slip) auf den Widerlagern bei großen Durchbiegungen vermieden werden (Bild 1).
| Bild 1: | Rutschen des Prüfkörpers auf den Widerlager bei großen Durchbiegungen |
Wie bei der Zug- oder Druckbeanspruchung sind auch bei der Biegebelastung die unterschiedlichen Deformationsanteile, die zeitlich und lastabhängig wirksam werden, bei der Bewertung der Messergebnisse zu berücksichtigen. In Abhängigkeit vom Typ des Kunststoffes treten ebenfalls linear-elastische, linear-viskoelastische, nichtlinear-viskoelastische und plastische Verformungsanteile auf, wobei das Verhältnis der Verformungsanteile in Bezug auf die Gesamtverformung vom jeweiligen Kunststoff sowie den Beanspruchungsbedingungen (Temperatur und Prüfgeschwindigkeit) abhängt. Demzufolge sind die im Biegeversuch ermittelten Kennwerte eine Funktion der Verformung, der Dehngeschwindigkeit, der Belastung oder Spannung, der Temperatur und des inneren Zustandes des Prüfkörpers.
Bestimmung des Biegemomentenverlaufs
Für die Auswertung des Biegeverhaltens und die Berechnung der Biegespannung sowie der zugehörigen Randfaserdehnungen wird die elastische Linie bei Kenntnis des Biegemomentenverlaufs (Dreipunkt- oder Vierpunktbiegelinie) herangezogen. Die Biegelinie des verformten Prüfkörpers ergibt sich nach Gl. (1) und Bild 2 wie folgt:
| (1) |
| Bild 2: | Biegelinie bei Dreipunktbiegung am deformierten Prüfkörper (Theorie 2. Ordnung) |
Da diese Differentialgleichung als auch die zugehörigen Randbedingungen von der Neigung der elastischen Linie abhängen, kann diese Gleichung nur auf numerischen Weg gelöst werden. Für eine ingenieurtechnisch handhabbare Lösung wurde deshalb die Nutzung der Biegelinie am unverformten Prüfkörper vereinbart. Damit wird die Neigung der Biegeline mit ds/dx ≈ 0 vernachlässigbar und es entsteht die vereinfachte Biegelinie nach Gl. (2) und Bild 3:
| (2) |
| Bild 3: | Biegelinie des undeformierten Prüfkörper (Theorie 1. Ordnung) |
Die Lösung dieser Differentialgleichung mit der Biegespannung σf und der Randfaserdehnung εf ist jedoch nur für kleine Durchbiegungen (s << h) gültig, weshalb in der prüftechnischen Praxis mit Durchbiegungen von bis zu 6 mm (s = 1,5 h, h = 4 mm) oftmals interpretative Probleme bei duktilen Kunststoffen entstehen. Die Anwendung dieser Auswertegleichungen setzt außerdem eine symmetrische Spannungs- und Dehnungsverteilung über den Querschnitt voraus, so dass die Nulllinie der Spannung oder Dehnung identisch mit der neutralen Faser des Biegebalkens ist. Infolge des teilweise sehr unterschiedlichen Zug- und Druckverhaltens der Kunststoffe (siehe PS) mit differierenden Fließspannungen σty und σcy kann es deshalb zu einer Verschiebung k der neutralen Faser (Bild 4) kommen, wodurch die Auswertegleichungen des Biegeversuchs eigentlich nicht mehr anwendbar sind.
| Bild 4: | Verschiebung der neutralen Faser bei unterschiedlichem Zug- und Druckverhalten |
Neben diesen Normalspannungen entstehen insbesondere bei dicken Prüfkörpern oder sehr geringen Stützweiten parabolisch über den Querschnitt verteilte Schubspannungen (Bild 5), die speziell bei Laminaten auf der Zugseite Delaminationen zwischen den Schichten verursachen können und zu fehlerbehafteten Kennwerten führen. Aus diesem Grund sollte das Stützweiten/Höhen-Verhältnis bei isotropen und homogenen Kunststoffen L = (16 ± 1) h betragen und bei Laminaten sollte ein Verhältnis von L = (20 – 25 ± 1) h eingehalten werden.
| Bild 5: | Auswirkungen von Schubspannungen im Querschnitt |
Eine umfassende Literaturanalyse zu den mechanischen Kennwerten εf, σfM und σfc bei Biegebeanspruchung für zahlreiche Kunststoffe ist in [3] enthalten.
Siehe auch
- Biegeversuch
- Biegemodul
- Dynamisch-Mechanische Analyse (DMA) – Biegebeanspruchung
- Biegestreifenverfahren
- Biegeversuch und Schallemissionsanalyse
- Randfaserdehnung
Literaturhinweise
| [1] | Bierögel, C.: Biegeversuch an Kunststoffen. In: Grellmann, W., Seidler, S. (Hrsg.): Kunststoffprüfung. Carl Hanser Verlag, München (2024) 4. Auflage, S. 141–151 (ISBN 978-3-446-44718-9; E-Book: ISBN 978-3-446-48105-3; siehe AMK-Büchersammlung unter A 23) |
| [2] | Szabó, I.: Einführung in die Technische Mechanik. Springer Verlag, Berlin, Heidelberg (1984) 8. Auflage, (ISBN 3-540-13293-7; siehe AMK-Büchersammlung unter T 15) |
| [3] | Bierögel, C., Grellmann, W.: Bend Loading. In: Grellmann, W., Seidler, S.: Mechanical and Thermomechanical Properties of Polymers. Landolt-Börnstein. Volume VIII/6A3, Springer Verlag, Berlin (2014) S. 164–191, (ISBN 978-3-642-55165-9; siehe AMK-Büchersammlung unter A 16) |

![{\displaystyle {\frac {s^{\prime \prime }(x)}{[1+s^{\prime 2}(x)]^{\frac {3}{2}}}}=-{\frac {M_{b}(x)}{E\ I_{y}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c34c56bc7aa8e81a5dd3f1176add4319341382c9)