Dynamisch-Mechanische Analyse (DMA) – Grundlagen: Unterschied zwischen den Versionen
Die Seite wurde neu angelegt: „{{PSM_Infobox}} <span style="font-size:1.2em;font-weight:bold;">Dynamisch-Mechanische Analyse (DMA) – Grundlagen</span> __FORCETOC__ ==Grundlagen== Bei der…“ |
Keine Bearbeitungszusammenfassung |
||
| (3 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 157: | Zeile 157: | ||
==Bestimmung der Glastemperatur T<sub>g</sub>== | ==Bestimmung der Glastemperatur T<sub>g</sub>== | ||
Im '''Bild 4''' sind schematische Modul-Temperatur-Diagramme unter Zugschwingbeanspruchung für verschiedene Typen von [[Kunststoffe]]n dargestellt, die auch bevorzugt zur Ermittlung der [[Glastemperatur|Glasübergangstemperatur T<sub>g</sub>]] benutzt werden. Bei den amorphen Kunststoffen ('''Bild 4a''') tritt infolge der hohen Mobilität der Ketten und Kettensegmente in der Regel ein deutlich ausgeprägter Übergangsbereich auf, bei dem die Glastemperatur relativ einfach bestimmbar ist. Aufgrund des kristallinen Anteils ist dieser Übergang in Abhängigkeit vom [[Kristallinitätsgrad]] weniger ausgeprägt ('''Bild 4b'''). Infolge des hohen Vernetzungsgrades von [[Duroplaste|Duromeren]], wie z. B. EP- oder UP-Harzen, ist der Glasübergang in der DMTA oftmals schlecht erkennbar ('''Bild 4c'''), während bei [[Elastomere|Elastomeren]] durch den viel geringeren Vernetzungsgrad die Glastemperatur besser bestimmbar ist ('''Bild 4d'''). | Im '''Bild 4''' sind schematische Modul-Temperatur-Diagramme unter Zugschwingbeanspruchung für verschiedene Typen von [[Kunststoffe]]n dargestellt, die auch bevorzugt zur Ermittlung der [[Glastemperatur|Glasübergangstemperatur T<sub>g</sub>]] benutzt werden. Bei den amorphen Kunststoffen ('''Bild 4a''') tritt infolge der hohen Mobilität der Ketten und Kettensegmente in der Regel ein deutlich ausgeprägter Übergangsbereich auf, bei dem die Glastemperatur relativ einfach bestimmbar ist. Aufgrund des kristallinen Anteils ist dieser Übergang in Abhängigkeit vom [[Kristallinität|Kristallinitätsgrad]] weniger ausgeprägt ('''Bild 4b'''). Infolge des hohen Vernetzungsgrades von [[Duroplaste|Duromeren]], wie z. B. EP- oder UP-Harzen, ist der Glasübergang in der DMTA oftmals schlecht erkennbar ('''Bild 4c'''), während bei [[Elastomere|Elastomeren]] durch den viel geringeren [[Vernetzung Elastomere|Vernetzungsgrad]] die [[Glastemperatur]] besser bestimmbar ist ('''Bild 4d'''). | ||
[[Datei:DMA_Grundlagen-4.jpg]] | [[Datei:DMA_Grundlagen-4.jpg]] | ||
| Zeile 181: | Zeile 181: | ||
|width="580px"|Verarbeitungsbereich | |width="580px"|Verarbeitungsbereich | ||
|} | |} | ||
==Siehe auch== | |||
*[[Dynamisch-Mechanische Analyse (DMA) – Biegebeanspruchung]] | |||
*[[Dynamisch-Mechanische Analyse (DMA) – Zugbeanspruchung]] | |||
*[[Dynamisch-Mechanische Analyse (DMA) – Torsionsbeanspruchung]] | |||
| Zeile 188: | Zeile 193: | ||
|-valign="top" | |-valign="top" | ||
|[1] | |[1] | ||
|Lüpke, T.: Grundlagen mechanischen Verhaltens. In: Grellmann, W., [[Seidler,_Sabine|Seidler, S.]] (Hrsg.): Kunststoffprüfung. Carl Hanser Verlag, München ( | |Lüpke, T.: Grundlagen mechanischen Verhaltens. In: [[Grellmann,_Wolfgang|Grellmann, W.]], [[Seidler,_Sabine|Seidler, S.]] (Hrsg.): Kunststoffprüfung. Carl Hanser Verlag, München (2024) 4. Auflage, S. 92–106 (ISBN 978-3-446-44718-9; E-Book: ISBN 978-3-446-48105-3; siehe [[AMK-Büchersammlung]] unter A 23) | ||
|-valign="top" | |-valign="top" | ||
|[2] | |[2] | ||
|DIN EN ISO 6721-1 ( | |DIN EN ISO 6721-1 (2019-09): Kunststoffe – Bestimmung dynamisch-mechanischer Eigenschaften – Teil 1: Allgemeine Grundlagen | ||
|} | |} | ||
[[Kategorie:Deformation]] | [[Kategorie:Deformation]] | ||
[[Kategorie:Thermoanalytische Methoden]] | [[Kategorie:Thermoanalytische Methoden]] | ||
Aktuelle Version vom 8. Oktober 2024, 08:44 Uhr
| Ein Service der |
|---|

|
| Polymer Service GmbH Merseburg |
| Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de |
| Unser Weiterbildungsangebot: https://www.psm-merseburg.de/weiterbildung |
| PSM bei Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg |
Dynamisch-Mechanische Analyse (DMA) – Grundlagen
Grundlagen
Bei der dynamisch-mechanischen Analyse (siehe auch Elastizitätsmodul) wird ein Prüfkörper mit einer vorgegebenen Geometrie einer periodisch wechselnden Beanspruchung ausgesetzt. Durch die Variation der Frequenz ist die Charakterisierung der Zeitabhängigkeit des Werkstoffverhaltens bei konstanter Temperatur möglich. Falls diese Untersuchungen in einer Temperierkammer durchgeführt werden, wird die Prüfmethode als DMTA bezeichnet und es wird die Temperaturabhängigkeit für die betreffenden Werkstoffe charakterisiert. Für den Zusammenhang zwischen der Beanspruchungszeit t und der Frequenz f bzw. Kreisfrequenz ω gilt die Beziehung nach Gl. (1).
| (1) |
Die DMA zeichnet sich dadurch aus, dass für die Ermittlung viskoelastischer Kennwerte in einem weiten Frequenzbereich nur relativ kurze Versuchszeiten erforderlich sind. Darüber hinaus ist es relativ einfach möglich, das Werkstoffverhalten in Abhängigkeit von der Temperatur mittels der dynamisch-mechanisch thermischen Analyse (DMTA) zu untersuchen, wobei hier aufgrund der notwendigen Temperaturstabilität längere Versuchszeiten erforderlich sind [1].
Durchführung der DMA
Für die Durchführung der DMA existieren unterschiedliche Varianten, die sich hinsichtlich des realisierbaren Frequenzbereiches, der Art der mechanischen Beanspruchung und der ermittelten Werkstoffkenngröße unterscheiden. Eine andere Einteilung ist in Abhängigkeit von der Art der Schwingungsanregung in die Verfahren
- mit erzwungenen Schwingungen,
- mit freien gedämpften Schwingungen und
- mit Resonanzschwingungen möglich.
Im Bereich sehr hoher Frequenzen wird darüber hinaus die Ausbreitung von Schall- und Ultraschallwellen oder die dielektrische Spektroskopie zur Kennwertermittlung verwendet. Die unterschiedlichen Methoden der DMA oder DMTA sind in der DIN EN ISO 6721-1 [2] standardisiert.
Verfahren mit erzwungenen Schwingungen
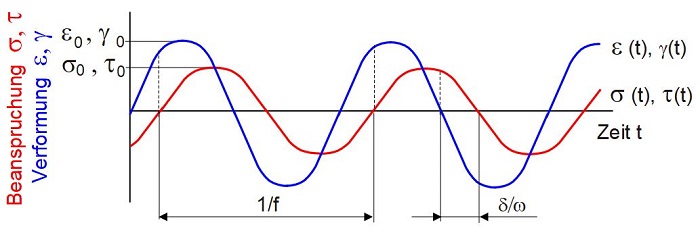
Für die Charakterisierung der viskoelastischen Eigenschaften von Kunststoffen unter Verwendung erzwungener Schwingungen wird der Prüfkörper einer sinusförmig wechselnden mechanischen Beanspruchung mit konstanter Frequenz und konstanter Amplitude ausgesetzt (Bild 1). Bei linear-viskoelastischem Verhalten weisen die zeitlichen Änderungen von Spannung und Deformation im eingeschwungenen Zustand die gleiche Frequenz aber unterschiedliche Phasenlagen auf.
| Bild 1: | Zeitliche Änderung von Spannung und Dehnung bei dynamisch-mechanischer Analyse unter Verwendung erzwungener Schwingungen |
Für den Fall einer Normalspannungsbeanspruchung gelten die Gln. (2) und (3) und bei der Schub- oder Scherbelastung sind die Gln. (4) und (5) anzuwenden.
| (2) |
| (3) |
| (4) |
| (5) |
Infolge der Phasenverschiebung δ zwischen Beanspruchung (Spannung) und der Verformung (Dehnung oder Scherung) ist zur Beschreibung des Spannungs-Dehnungs- (Scherungs-) Zusammenhanges der Modul als komplexe Größe E* oder G* nach den Gln. (6) und (7) einzuführen.
| (6) |
| (7) |
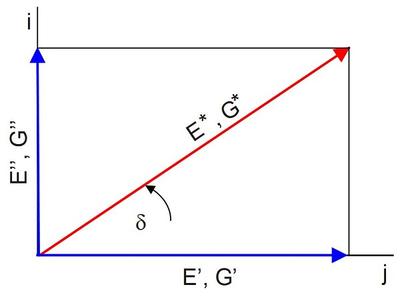
Der komplexe Modul kann als Vektor in der komplexen Zahlenebene betrachtet werden (Bild 2), dessen Richtung durch den Phasenwinkel δ und dessen Betrag durch das Verhältnis der Amplitudenwerte von Spannung und Dehnung gegeben ist.
| Bild 2: | Darstellung der Moduli E* und G* in der komplexen Zahlenebene |
Der Absolutbetrag des jeweiligen Moduls ergibt sich aus dem Verhältnis der Initialbeanspruchung zur Ausgangsverformung nach den Gln. (8) und (9).
| (8) |
| (9) |
Unter Verwendung einfacher trigonometrischer Beziehungen ist eine Aufteilung in Realteil E‘ oder G‘ und Imaginärteil E‘‘ oder G‘‘ möglich, die mit den Gln. (10) bis (13) vorgenommen wird. Der Realteil E‘ oder G‘ wird als Speichermodul bezeichnet und ist ein Maß für die während einer Schwingungsperiode gespeicherte reversible Energie Wrev. Der Imaginäranteil E‘‘ oder G‘‘ erfasst die in der Periode dissipierte Energie Wirrev und wird als Verlustmodul benannt. Aus dem Verhältnis von Verlust- und Speichermodul ergibt sich der Verlustfaktor d = tan δ, welcher das Dämpfungsverhalten des Werkstoffs nach den Gln. (14) und (15) charakterisiert.
| (10) |
| (11) |
| (12) |
| (13) |
| (14) |
| (15) |
Das Verfahren der erzwungenen Schwingungen ist auf Frequenzen unterhalb der Resonanzfrequenz des Prüfkörpers beschränkt. Kommerzielle Geräte arbeiten im Bereich von ca. 10-2 Hz bis 102 Hz, wobei als Messgröße die Leistungsaufnahme des Antriebmotors dient. Die Messung kann sowohl dehnungs- als auch spannungsgeregelt erfolgen, was die Bestimmung des komplexen Moduls E* oder G* und der komplexen Nachgiebigkeit C* = 1 / E* ermöglicht. Durch axial und torsional arbeitende Prüfgeräte kann unter Verwendung einer entsprechenden Prüfkörperaufnahme eine Vielzahl unterschiedlicher Beanspruchungsfälle (Zug, Druck, Biegung, Scherung und Torsion) realisiert werden. Dies gestattet die Ermittlung komplexer Elastizitäts- und Schermoduli in einem weiten Steifigkeitsbereich von 10-3 MPa bis 106 MPa. Der größte Nachteil des Verfahrens liegt allerdings in der geringen Empfindlichkeit bei der Messung kleiner Dämpfungen (tan δ < 0,01), also sehr steifer oder hochmoduliger Werkstoffe. Auf Grund ihrer großen Anwendungsbreite besitzen Verfahren mit erzwungenen Schwingungen heute eine dominierende Rolle bei der dynamisch-mechanischen Analyse polymerer Werkstoffe.
Verfahren mit freien gedämpften Schwingungen
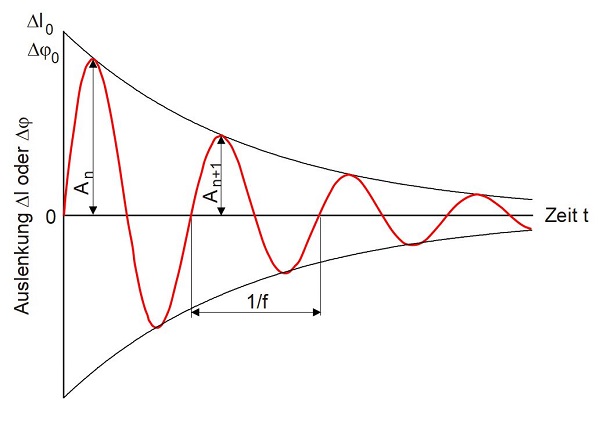
Die freien gedämpften Schwingungen werden eigentlich nur bei Messungen mit dem Torsionspendel angewandt, wobei hier wesentlich niedrige Messfrequenzen möglich sind. Wird ein Prüfkörper durch eine einmalige impulsartige Verformung aus seiner Ruhelage ausgelenkt, so kehrt er in freien gedämpften Schwingungen in den Gleichgewichtszustand zurück. Die Eigenfrequenz der Schwingung sowie die zeitliche Abnahme der Schwingungsamplituden sind dabei von den viskoelastischen Eigenschaften des Werkstoffs und der Prüftemperatur abhängig (Bild 3). Die freien gedämpften Schwingungen werden bei Frequenzen im Bereich von 0,1 bis 10 Hz genutzt, wobei hier die Untersuchung von Werkstoffen mit geringer Dämpfung von tan δ ≤ 0,1 bevorzugt wird.
| Bild 3: | Frei abklingende gedämpfte Schwingung |
Da bei Untersuchungen in Abhängigkeit von der Temperatur durch die Moduländerung eine Veränderung der Eigenfrequenz des Systems stattfindet, werden Modul-Temperatur-Kurven deshalb in der Regel bei gleitender Frequenz gemessen. Allerdings ist eine Kompensation der Frequenzänderungen über Variation des Trägheitsmoments der Schwungmasse prinzipiell möglich. Die wesentlichen Vorteile des Torsionspendels bestehen in der Einfachheit von Aufbau und Messwerterfassung sowie in der hohen Empfindlichkeit.
Resonanzverfahren
Werden erzwungene Schwingungen mit einer Frequenz erzeugt, deren Wellenlänge die Größe der Prüfkörperabmessungen erreicht, so kommt es zu Resonanzerscheinungen. Erfolgt die Anregung des Prüfkörpers im Resonanzgebiet mit einer konstanten Kraftamplitude, so durchläuft die Amplitude der Auslenkung ein Maximum, wobei hier die jeweilige Resonanzfrequenz fi und die Halbwertsbreite Δfi ermittelt werden, die in Zusammenhang mit den viskoelastischen Eigenschaften des untersuchten Werkstoffs stehen. Erzwungener Resonanzschwingungen zur Bestimmung des komplexen Moduls werden bevorzugt im Biege- oder Zugschwingversuch angewandt. Die Anregung kann servohydraulisch, kapazitiv oder elektromagnetisch erfolgen und die Messung der Schwingungen wird zumeist berührungsfrei über elektromagnetische Wandler durchgeführt.
Bestimmung der Glastemperatur Tg
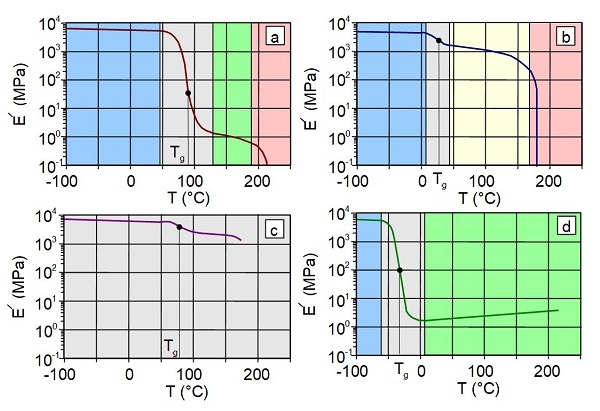
Im Bild 4 sind schematische Modul-Temperatur-Diagramme unter Zugschwingbeanspruchung für verschiedene Typen von Kunststoffen dargestellt, die auch bevorzugt zur Ermittlung der Glasübergangstemperatur Tg benutzt werden. Bei den amorphen Kunststoffen (Bild 4a) tritt infolge der hohen Mobilität der Ketten und Kettensegmente in der Regel ein deutlich ausgeprägter Übergangsbereich auf, bei dem die Glastemperatur relativ einfach bestimmbar ist. Aufgrund des kristallinen Anteils ist dieser Übergang in Abhängigkeit vom Kristallinitätsgrad weniger ausgeprägt (Bild 4b). Infolge des hohen Vernetzungsgrades von Duromeren, wie z. B. EP- oder UP-Harzen, ist der Glasübergang in der DMTA oftmals schlecht erkennbar (Bild 4c), während bei Elastomeren durch den viel geringeren Vernetzungsgrad die Glastemperatur besser bestimmbar ist (Bild 4d).
| Bild 4: | Schematische Speichermodul-Temperatur-Kurven von (a) – amorphen, (b) – teilkristallinen Thermoplasten, (c) duromeren und (d) elastomeren Kunststoffen | ||
| ∎ | – | Glaszustand | |
| ∎ | – | Glasübergangsbereich | |
| ∎ | – | Gummielastizität | |
| ∎ | – | Verarbeitungsbereich | |
Siehe auch
- Dynamisch-Mechanische Analyse (DMA) – Biegebeanspruchung
- Dynamisch-Mechanische Analyse (DMA) – Zugbeanspruchung
- Dynamisch-Mechanische Analyse (DMA) – Torsionsbeanspruchung
Literaturhinweise
| [1] | Lüpke, T.: Grundlagen mechanischen Verhaltens. In: Grellmann, W., Seidler, S. (Hrsg.): Kunststoffprüfung. Carl Hanser Verlag, München (2024) 4. Auflage, S. 92–106 (ISBN 978-3-446-44718-9; E-Book: ISBN 978-3-446-48105-3; siehe AMK-Büchersammlung unter A 23) |
| [2] | DIN EN ISO 6721-1 (2019-09): Kunststoffe – Bestimmung dynamisch-mechanischer Eigenschaften – Teil 1: Allgemeine Grundlagen |