Plastische Zone: Unterschied zwischen den Versionen
Die Seite wurde neu angelegt: „{{PSM_Infobox}} <span style="font-size:1.2em;font-weight:bold;">Plastische Zone (siehe auch: Bruchprozesszone)</span> __FORCETOC__ ==Ausbildung der plastische…“ |
Keine Bearbeitungszusammenfassung |
||
| Zeile 1: | Zeile 1: | ||
{{PSM_Infobox}} | {{PSM_Infobox}} | ||
<span style="font-size:1.2em;font-weight:bold;">Plastische Zone (siehe auch: [[Bruchprozesszone]]) | <span style="font-size:1.2em;font-weight:bold;">Plastische Zone</span><br> | ||
(siehe auch: [[Bruchprozesszone]]) | |||
__FORCETOC__ | __FORCETOC__ | ||
==Ausbildung der plastischen Zone (Dog-Bone-Modell)== | ==Ausbildung der plastischen Zone (Dog-Bone-Modell)== | ||
Das linear-elastische oder auch rein [[Deformation#elastische Deformation|elastische Deformation]]sverhalten ist eine idealisierte Modellvorstellung. Dieses Werkstoffverhalten wird mit der [[Bruchmechanik#Linear-elastische_Bruchmechanik|linear-elastischen Bruchmechanik (LEBM)]] beschrieben, die auf dem kontinuumsmechanischen [[Rissmodell nach GRIFFITH]] beruht. Dabei bleiben die realen Prozesse der [[Rissausbreitung]] in makroskopischen Bereichen an der Spitze eines [[Riss]]es zunächst unberücksichtigt. Von [[Blumenauer, Horst|Blumenauer]] [1] wird beschrieben, dass auch bei makroskopisch spröden Werkstoffverhalten die mechanische [[Beanspruchung]] zur Spannungsüberhöhung an der [[Riss]]spitze führen kann und in deren Folge vor der Rissspitze [[plastische Deformation|plastische Deformationen]] auftreten. In Abhängigkeit von der [[Mikroskopische Struktur|Mikrostruktur]] des Werkstoffes kommt es zur Ausbildung in Form und Größe unterschiedlicher plastischer Zonen, die in der [[Bruchmechanische Prüfung|bruchmechanischen Werkstoffprüfung]] bei der Ermittlung dementsprechender [[Kennwert]]e berücksichtigt werden muss. | Das linear-elastische oder auch rein [[Deformation#elastische Deformation|elastische Deformation]]sverhalten ist eine idealisierte Modellvorstellung. Dieses Werkstoffverhalten wird mit der [[Bruchmechanik#Linear-elastische_Bruchmechanik|linear-elastischen Bruchmechanik (LEBM)]] beschrieben, die auf dem kontinuumsmechanischen [[Rissmodell nach GRIFFITH]] beruht. Dabei bleiben die realen Prozesse der [[Rissausbreitung]] in makroskopischen Bereichen an der Spitze eines [[Riss]]es zunächst unberücksichtigt. Von [[Blumenauer, Horst|Blumenauer]] [1] wird beschrieben, dass auch bei makroskopisch spröden Werkstoffverhalten die mechanische [[Beanspruchung]] zur Spannungsüberhöhung an der [[Riss]]spitze führen kann und in deren Folge vor der Rissspitze [[plastische Deformation|plastische Deformationen]] auftreten. In Abhängigkeit von der [[Mikroskopische Struktur|Mikrostruktur]] des Werkstoffes kommt es zur Ausbildung in Form und Größe unterschiedlicher plastischer Zonen, die in der [[Bruchmechanische Prüfung|bruchmechanischen Werkstoffprüfung]] bei der Ermittlung dementsprechender [[Kennwert]]e berücksichtigt werden muss. | ||
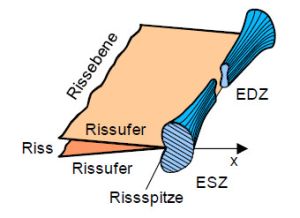
Bei der in '''Bild 1''' dargestellten idealisierten Form einer plastischen Zone ist die Ausdehnung im Inneren und an der [[Oberfläche]] geringer, was auf dem von innen nach außen abfallenden [[Bruchmechanik|Spannungsintensitätsfaktor]] zurückgeführt werden kann. | |||
[[Datei:plastische_zone1.jpg]] | [[Datei:plastische_zone1.jpg]] | ||
| Zeile 12: | Zeile 15: | ||
|width="600px" |Idealisierte Form der plastischen Zone bei Kleinbereichsfließen („Hundeknochen“-Form) | |width="600px" |Idealisierte Form der plastischen Zone bei Kleinbereichsfließen („Hundeknochen“-Form) | ||
|} | |} | ||
Aus dem Übergang vom [[Ebener Spannungszustand|ebenen Spannungszustand (ESZ)]] zum ebenen Dehnungszustand (EDZ) im Inneren ergibt sich die von [[Rissmodell nach IRWIN und Mc CLINTOCK|Irwin- und Mc Clintock]] abgeleitete sogenannte „Hundeknochen“-Form (engl.: Dog Bone) der plastischen Zone. | Aus dem Übergang vom [[Ebener Spannungszustand|ebenen Spannungszustand (ESZ)]] zum ebenen Dehnungszustand (EDZ) im Inneren ergibt sich die von [[Rissmodell nach IRWIN und Mc CLINTOCK|Irwin- und Mc Clintock]] abgeleitete sogenannte „Hundeknochen“-Form (engl.: Dog Bone) der plastischen Zone. | ||
Version vom 16. Februar 2018, 15:39 Uhr
| Ein Service der |
|---|

|
| Polymer Service GmbH Merseburg |
| Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de |
| Unser Weiterbildungsangebot: https://www.psm-merseburg.de/weiterbildung |
| PSM bei Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg |
Plastische Zone
(siehe auch: Bruchprozesszone)
Ausbildung der plastischen Zone (Dog-Bone-Modell)
Das linear-elastische oder auch rein elastische Deformationsverhalten ist eine idealisierte Modellvorstellung. Dieses Werkstoffverhalten wird mit der linear-elastischen Bruchmechanik (LEBM) beschrieben, die auf dem kontinuumsmechanischen Rissmodell nach GRIFFITH beruht. Dabei bleiben die realen Prozesse der Rissausbreitung in makroskopischen Bereichen an der Spitze eines Risses zunächst unberücksichtigt. Von Blumenauer [1] wird beschrieben, dass auch bei makroskopisch spröden Werkstoffverhalten die mechanische Beanspruchung zur Spannungsüberhöhung an der Rissspitze führen kann und in deren Folge vor der Rissspitze plastische Deformationen auftreten. In Abhängigkeit von der Mikrostruktur des Werkstoffes kommt es zur Ausbildung in Form und Größe unterschiedlicher plastischer Zonen, die in der bruchmechanischen Werkstoffprüfung bei der Ermittlung dementsprechender Kennwerte berücksichtigt werden muss.
Bei der in Bild 1 dargestellten idealisierten Form einer plastischen Zone ist die Ausdehnung im Inneren und an der Oberfläche geringer, was auf dem von innen nach außen abfallenden Spannungsintensitätsfaktor zurückgeführt werden kann.
| Bild 1: | Idealisierte Form der plastischen Zone bei Kleinbereichsfließen („Hundeknochen“-Form) |
Aus dem Übergang vom ebenen Spannungszustand (ESZ) zum ebenen Dehnungszustand (EDZ) im Inneren ergibt sich die von Irwin- und Mc Clintock abgeleitete sogenannte „Hundeknochen“-Form (engl.: Dog Bone) der plastischen Zone.
Berücksichtigung der plastischen Zone in der bruchmechanischen Kennwertermittlung
Die Ausdehnung dieser plastischen Zone muss im Vergleich mit der Ausdehnung der Ausgangsrisslänge in einem Prüfkörper oder den Bauteilabmessungen relativ klein sein. Die Berücksichtigung in der Kennwertermittlung erfolgt über die sogenannte effektive Risslänge aeff nach der Gleichung (1).
| (1) |
Damit wird formal der Übergang von der linear-elastischen Bruchmechanik (LEBM) zur LEBM mit Kleinbereichsfließen vollzogen.
Die Gleichung (2) für die Bestimmung des Spannungsintensitätsfaktors lautet:
| (2) |
Die Größe der plastischen Zone im Ligament lässt sich grob abschätzen, wenn in den SNEDDON-Gleichungen die Spannung durch die Streckgrenze Re ersetzt wird.
| für ESZ | (3) |
| für EDZ | (4) |
Beispiel einer plastischen Zone für PVC-C
Die Ausbildung der plastischen Zone erweist sich für Kunststoffe als abhängig von der Mikrostruktur und wurde z. B. für einen nachchlorierten Polyvinylchlorid-Werkstoff (Kurzzeichen: PVC-C oder PVCC) [3, 4] mit der Beziehung (5)
| (5) |
beschrieben.
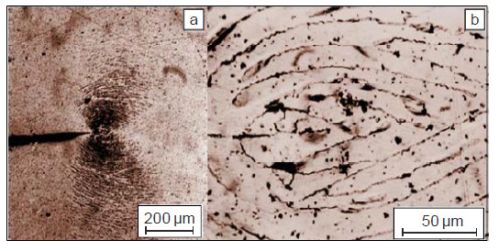
Im Bild 2 wird das sich im instrumentierten Kerbschlagbiegeversuch bei schlagartig beanspruchten SENB-Prüfkörpern ausbildende Deformationsgebiet vor der Rissspitze gezeigt. Nach der Kerbeinbringung wurden die Prüfkörper poliert und mit Gold bedampft. Dabei zeigen die Risse die Ausdehnung des Deformationsgebietes an.
| Bild 2: | Deformationsgebiet an der Rissspitze eines nachchlorierten Polyvinylchlorid-Werkstoffes (Kurzzeichen: PVC-C) Gesamtansicht (a) und Ausschnitt an der Rissspitze (b) eines SENB-Prüfkörpers nach schlagartiger Beanspruchung (KI < KId), poliert und mit Gold bedampft |
Literaturhinweise
| [1] | Blumenauer, H., Pusch, G.: Technische Bruchmechanik, Deutscher Verlag für Grundstoffindustrie, Leipzig Stuttgart (1993), (ISBN 3-342-00659-5; siehe AMK-Büchersammlung unter E 29-3) |
| [2] | Anderson, T. L.: Fracture Mechanics. Fundamentals and Applications. 3rd Ed., CRC Press Boca Raton (2005) (ISBN 978-0-8493-1656-2; siehe AMK-Büchersammlung unter E 8-2) |
| [3] | Jungbluth, M.: Untersuchungen zum Verformungs- und Bruchverhalten von PVC-Werkstoffen. Dissertation, TH Leuna-Merseburg (siehe AMK-Büchersammlung unter B 1-1) |
| [4] | Grellmann, W.; Seidler, S. (Hrsg.): Kunststoffprüfung. Carl Hanser Verlag, München (2015) 3. Auflage, S. 255/256 (ISBN 978-3-446-44350-1; siehe AMK-Büchersammlung unter A 18) |