Äquivalentenergiekonzept

Äquivalentenergiekonzept

Grundlagen

Das Äquivalentenergiekonzept von Witt und Mager [1,2] ist hinsichtlich seiner Aussagemöglichkeiten in die linear-elastischen Methoden der Bruchmechanik einzuordnen [3]. Die Entwicklung und Anwendung des J-Integral-Konzeptes hat die Äquivalentenergiemethode in den Hintergrund treten lassen, so dass sie zumeist in neueren Büchern [4] auch nicht mehr erwähnt wird.

Das von Witt und Mager auf der Grundlage eines Energievergleiches im elastisch-plastischen Spannungszustand entwickelte Konzept geht von der Untersuchung des Verformungsverhaltens von geometrisch ähnlichen, aber unterschiedlich dicken Prüfkörpern mit Rissen aus.

An diesen Prüfkörpern werden Kraft-Kraftangriffspunktverschiebungs-Kurven aufgenommen und die zum Bruch der Prüfkörper benötigten Kräfte F und die dabei auftretenden Durchbiegungen f bzw. allgemeinen Verschiebungen v werden registriert und in einem Diagramm gegeneinander aufgetragen.

Verwendet man eine Darstellung in Normkoordinaten (bezogenen Koordinaten), so lässt sich das Verformungsverhalten aller Prüfkörper in einer einzigen Abhängigkeit darstellen.

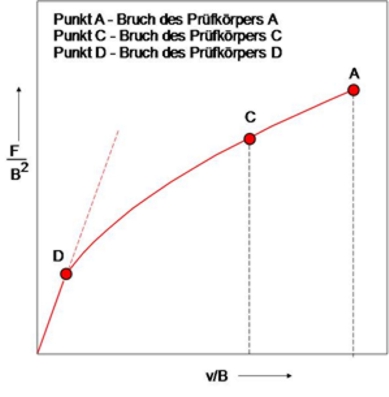
Bild 1: Kraft-Kraftangriffspunktverschiebungs-Kurve in bezogenen Koordinaten F/B₂ und v/B für geometrisch ähnliche Prüfkörper A, C und D mit unterschiedlicher Dicke

Grundannahme

Das Verhältnis der volumenbezogenen Bruchenergie ist gleich dem reziproken Verhältnis der Dickenabhängigkeit.

Voraussetzungen

1. A, C und D sind geometrisch ähnliche Prüfkörper
   
2. B_D > B_C > B_A; An den Punkten A, C und D erfolgt der Bruch der entsprechenden Prüfkörper
   
3. Während der Bruch des Prüfkörpers mit der Dicke BD noch rein elastisch ist, wächst mit abnehmender Dicke das Verhältnis der Energien beim Bruch bezogen auf Probe D an.

Aus der zum Bruch eines kleinen Prüfkörpers mit elastisch-plastischer Verformung notwendigen Energie kann nun auf die Energie, die zum Bruch eines großen Prüfkörpers mit elastischer Verformung notwendig ist, geschlossen werden. Die Fläche unter dieser Kurve hat die Dimension einer auf das Volumen bezogenen Energie, weshalb sie daher auch als volumetrische Energie bezeichnet wird. Aus diesem Grund könnte man diese Aussage auch auf die volumetrische Energie beziehen. Die experimentelle Bestimmung des K-Faktors erfolgt über die Ermittlung einer pseudoelastischen Kraft $F_{Q}^{*}$.

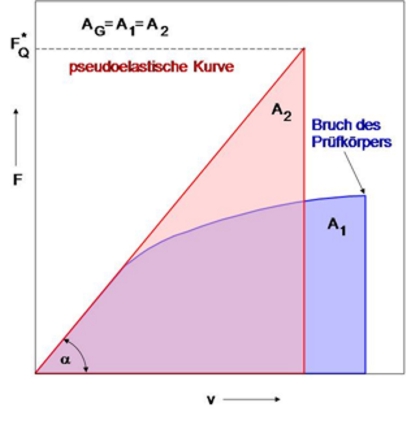
Bild 2: Bestimmung der pseudoelastischen Kraft $F_{Q}^{*}$ nach dem Äquivalentenergiekonzept

Zunächst wird der Flächeninhalt A₁ unter der Kraft-Kraftangriffspunktverschiebungs-Kurve – im Falle des instrumentierten Kerbschlagbiegeversuches wäre dies die Schlagkraft-Durchbiegungs-Kurve – bestimmt. Dann wird durch Anlegen der Tangente an die Kraft-Kraftangriffspunktverschiebungs-Kurve unter Berücksichtigung der Flächengleichheit A₁ ≡ A₂ die pseudoelastische Kraft nach der Gleichung

$F_{Q}^{*}={\sqrt {2A_{1}tan\,\alpha }}$

berechnet. Entsprechend Bild 2 ist tan α der Anstieg der Kraft-Kraftangriffspunkt-verschiebungs-Kurve bei CT- und SENT-Prüfkörpern bzw. der Kraft-Durchbiegungs-Kurven bei Dreipunktbiegeprüfkörpern.

Für die Gleichung der Spannungsintensitätsfaktoren für die einzelnen Prüfkörper erhält man unter Vernachlässigung der Herleitung:

A. Dreipunktbiegeprüfkörper (SENB – Single Edge Notch Bend)

$K_{I}^{E}={\frac {F_{Q}^{*}\,\cdot \,s}{B\,\cdot \,W^{3/2}}}f\left({\frac {a_{eff}}{W}}\right)$

mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://de.wikipedia.org/api/rest_v1/“:): {\displaystyle f\left(\frac{a}{W}\right)\, = \,2,9\,\left(\frac{a}{W}\right)^{1/2} – 4,6\,\left(\frac{a}{W}\right)^{3/2} \,+ \,21,8\left(\frac{a}{W}\right)^{5/2}\,– \,37,6 \left(\frac{a}{W}\right)^{7/2} \,+ \,38,7\left(\frac{a}{W}\right)^{9/2}}

und $a\,=\,a_{eff}$

B. Kompaktzugprüfkörper (CT-Prüfkörper – Compact Tension)

$K_{I}^{E}={\frac {F_{Q}^{*}}{B\,\cdot \,W^{1/2}}}f\left({\frac {a_{eff}}{W}}\right)$

mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://de.wikipedia.org/api/rest_v1/“:): {\displaystyle f\left(\frac{a}{W}\right)\, = \,29,6\,\left(\frac{a}{W}\right)^{1/2}\,–\, 1855\left(\frac{a}{W}\right)^{3/2}\,+ \,655,7\left(\frac{a}{W}\right)^{5/2}\,– \,1017\left(\frac{a}{W}\right)^{7/2}\,+\, 638,9\left(\frac{a}{W}\right)^{9/2}}

und $a\,=\,a_{eff}$

C. Einseitig gekerbter Zugprüfkörper (SENT-Prüfkörper (Single Edge Notched Tension)

$K_{I}^{E}={\frac {F_{Q}^{*}\,\cdot \,a^{1/2}}{B\,\cdot \,W}}f\left({\frac {a_{eff}}{W}}\right)$

mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://de.wikipedia.org/api/rest_v1/“:): {\displaystyle f\left(\frac{a}{W}\right)\, = \,1,99\,–\, 0,41\left(\frac{a}{W}\right)\,+\, 18,7\left(\frac{a}{W}\right)^{2}\,–\, 38,48\left(\frac{a}{W}\right)^{3}\,+ \,53,85\left(\frac{a}{W}\right)^{4}\,}

und $a\,=\,a_{eff}$

Die Überprüfung der Geometrieunabhängigkeit erfolgt über die Beziehungen

$a_{eff},B_{min},(W-a)\geq \beta \left({\frac {K_{Q}^{E}}{R_{e}}}\right)^{2}$

mit β als werkstoffabhängige Konstante: 0,6 …. 8,3 [5] bzw.

$a_{eff},B,(W-a)\geq \beta _{1}{\frac {(K_{Q}^{E})^{2}}{R_{e}\cdot E}}$

mit β₁ = 15 …..125 [5,6], die auch als Geometriekriterium oder vereinfachend als Dickenkriterium bezeichnet werden.

Anwendungsgrenzen

Das Äquivalentenergiekonzept beruht auf der Annahme, dass die Kraft-Kraftangriffspunktverschiebungs-Kurven geometrisch ähnlicher, aber unterschiedlich dicker Prüfkörper auf einer gemeinsamen Kurve liegen. Zur Verdeutlichung der Aussagekraft des Äquivalentenergiekonzeptes und damit der Grenzen seiner Anwendbarkeit werden zwei konkrete Beispiele betrachtet [7].

Beispiel 1

Werkstoffsystem:	PE-HD + GF (E-Glas)
Matrix	ρ = 0,960 gcm-3; MW = 87.300 g mol-1
Füllstoffvolumenanteile:	0,09; 0,14 und 0,28
Faserlänge:	l = 200 µm
Faserdurchmesser:	d = 10 µm
l/d-Verhältnis:	20
experimentelle Methode:	Instrumentierter Kerbschlagbiegeversuch (IKBV) und Aufnahme von Kraft (F)-Durchbiegungs(f)-Kurven
Bedingungen:	Stützweite/ Prüfkörperbreite (s/W) = 4 Hammergeschwindigkeit = 1 m s-1 Kerbtiefe/ Prüfkörperbreite (a/W) = 0,2
Messgrößen:	Fmax – maximale Kraft beim Einsetzen instabiler Rissausbreitung fmax – maximale Durchbiegung $F_{Q}^{*}$ – Pseudoelastische Kraft

Experimentelle Ergebnisse:

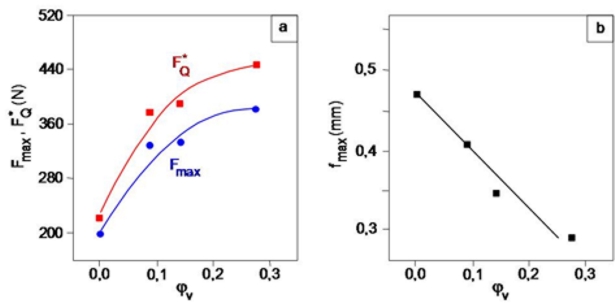
Bild 3: Abhängigkeit der maximalen Bruchkraft Fmax und der pseudoelastischen Kraft $F_{Q}^{*}$ (a) und der maximalen Durchbiegung fmax vom Faservolumenanteil für PE-HD + GF-Verbunde (b)

Zur Bestimmung bruchmechanischer Kennwerte der kritischen Spannungsintensitätsfaktoren K_I

$K_{I}=\sigma (\pi \cdot a)^{1/2}\,f\left({\frac {a_{eff}}{W}}\right)$

gelten die nachfolgend aufgeführten Bestimmungsgleichungen (SENB-Prüfkörper):

*LEBM: 

$K_{I}^{LEBM}={\frac {F_{max}\,\cdot \,s}{B\,\cdot \,W^{3/2}}}f\left({\frac {a}{W}}\right)$

*LEBM mit Kleinbereichsfließen:

$K_{I}^{LEBM}={\frac {F_{max}\,\cdot \,s}{B\,\cdot \,W^{3/2}}}f\left({\frac {a_{eff}}{W}}\right)$

*Äquivalentenergiekonzept:

$K_{I}^{E}={\frac {F_{Q}^{*}\,\cdot \,s}{B\,\cdot \,W^{3/2}}}f\left({\frac {a_{eff}}{W}}\right)$

(Gleichung für die Geometriefunktion siehe oben)

Experimentelle Ergebnisse:

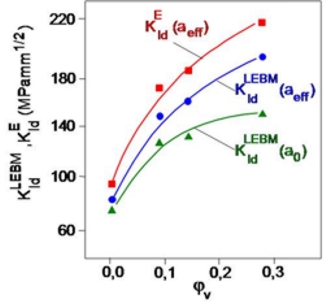
Bild 4: Abhängigkeit der verschiedenen kritischen Spannungsintensitätsfaktoren vom Faservolumenanteil für PE-HD + GF-Verbunde

Aus der vergleichenden Betrachtung von Bild 3 und Bild 4 wird deutlich, dass der kritische Spannungsintensitätsfaktor eine kraft- bzw. spannungsdeterminierte Kenngröße ist. Als direkte Messgröße geht entsprechend den Bestimmungsgleichungen nur die maximale Schlagkraft bzw. die pseudoelastische Kraft in die Berechnung ein.

Bei größeren plastischen Verformungen ist der Spannungsintensitätsfaktor nur eine formale Rechengröße, die weder qualitativ noch quantitativ zur Beschreibung der Zähigkeit ausreicht, da das Verformungsverhalten nicht berücksichtigt wird.

Der auf der Bruchfläche lichtmikroskopisch ermittelte Bruchspiegel zeigt die im Bild 5 dargestellte Abhängigkeit.

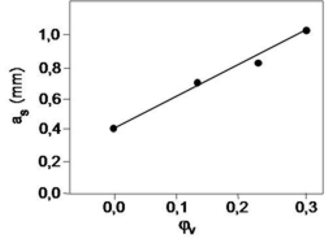
Bild 5: Abhängigkeit des Bruchspiegels a_s vom Faservolumenanteil für PE-HD+GF- Verbunde

Die Berücksichtigung des Anteils an stabilen Risswachstums in Form des Bruchspiegels führt zur Erhöhung der effektiven Risslänge a_eff. Die Ausgangsrisslänge in diesen Werkstoffen betrug 2 mm, d.h. man kann davon ausgehen, dass die Bedingung einer im Vergleich zur Ausgangsrisslänge kleinen plastischen Zone nicht erfüllt ist. Bei solchen Abhängigkeiten wie hier im Beispiel gezeigt, können durch die Betrachtungen der Messgrößen mehr Informationen über das Werkstoffverhalten gewonnen werden, als mit der bruchmechanischen Werkstoffkenngröße K_Id. Da die Messgrößen jedoch geometrieabhängige Größen sind, muss nach einem anderen Weg gesucht werden, um das Zähigkeitsverhalten dieser Verbunde quantitativ zu beschreiben.

Die kritische Rissöffnungsverschiebung ist geeignet um die Verformungsfähigkeit der Werkstoffe zu beschreiben.

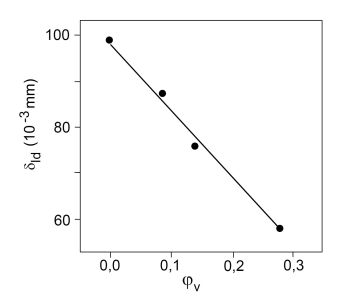
Bild 6: Abhängigkeit der kritischen Rissöffnungsverschiebung δ_Id vom Faservolumenanteil φ_v für PE-HD+GF-Verbunde

Die Kenngröße „kritische Rissöffnungsverschiebung“ ist immer dann vorteilhaft einsetzbar, wenn der Werkstoffanwender oder -entwickler eine Kenngröße sucht, die die zunehmende Versprödung deutlich beschreibt und eine geometrieunabhängige Größe darstellt.

Aus den bisherigen Darstellungen kann abgeleitet werden, dass die Grenze der Eignung des Äquivalentenergiekonzeptes erreicht ist, wenn es zu einer Verformungsbehinderung kommt, die sich in einer Abnahme der kritischen Rissöffnungsverschiebung äußert. Wenn eine kraftbestimmte und eine verformungsbestimmte Zähigkeitsbewertung zu unterschiedlichen Aussagen führt, muss für die energiebestimmte Bewertung des Bruchverhaltens eine Kenngröße gefunden werden, welche die Messgrößen Kraft und Durchbiegung in den Auswertegleichungen berücksichtigt.

Für eine derartige bruchmechanische Bewertung kann das J-Integral herangezogen werden. Dabei erweist sich für Polymerwerkstoffe die J-Integral-Auswertemethode nach Sumpter und Turner [8] als geeignet.

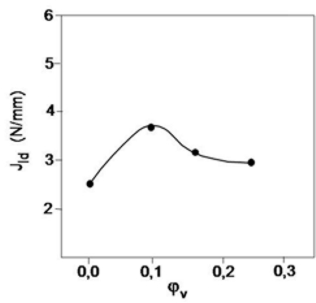
Bild 7: Abhängigkeit der J_{Id-Werte vom Faservolumenanteil für PE-HD+GF-Verbunde}

Von entscheidender Bedeutung für die Bewertung des Versagensprozess dieses PE-HD+GF-Verbundsystems ist die Abnahme der Ausgangsverformungsfähigkeit um ca. 40 %. Dieser Einfluss wird im Verlauf der J-Integralkenngröße widergespiegelt, wobei sich ein Maximum in den J-Werten (siehe Bild 7) für φ_v ≈ 0,1 einstellt.

Der Versagensprozess von kurzfaserverstärkten Kunststoffen ist durch verschiedene mikromechanische Bruchmoden, wie dem Aufreißen der Bindungen am Faserende und entlang der Faser/Matrix-Grenzfläche, dem Einsetzen von Gleitprozessen zwischen Faser und Matrix entlang einer werkstoffspezifischen Abgleitlänge, durch stabiles plastisches Matrixfließen ohne pull-out der Fasern, sowie lokalen Sprödbruch der Matrix mit pull-out der Fasern, gekennzeichnet [9].

Beispiel 2:

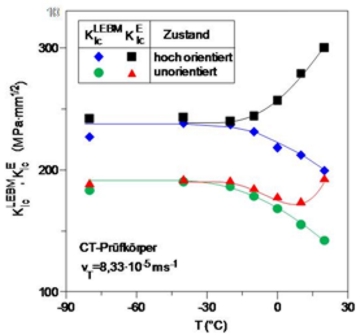
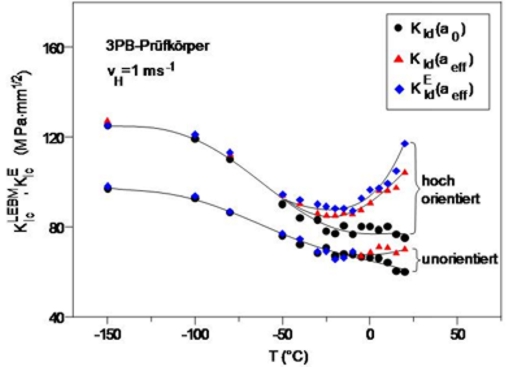
Werkstoffsystem: unorientiertes und hochorientiertes Polypropylen [10] (Kaltwalzen; Orientierungsgrad f_x = 80 %)

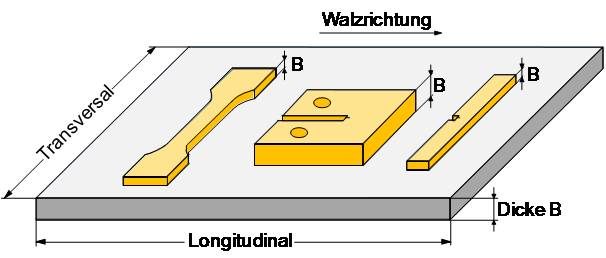
Bild 8: Anordnung der Prüfkörper und der Kerben in Dreipunktbiegeprüfkörpern und CT-Prüfkörpern in Bezug auf die Walzrichtung

Experimentelle Ergebnisse:

• statische Beanspruchung

• dynamische Beanspruchung

Literaturhinweise

• 1. Witt, F.J., Mager, T. R.: Nucl. Eng. Des. 17 (1971) S. 91
• 2. Witt, F.J.: Nucl. Eng. Des. 20 (1972) S. 237
• 3. Grellmann, W.: In: Schmiedel, H. (Hrsg.): Handbuch der Kunststoffprüfung. Carl Hanser Verlag München Wien (1992) S. 145/146 und 175
• 4. Grellmann, W., Seidler, S. (Hrsg.): Kunststoffprüfung. Carl Hanser Verlag München Wien (2005)
• 5. Eigene Ergebnisse, unveröffentlicht
• 6. Grellmann, W., Che, M.: Assessment of Temperature-Dependent Fracture Behaviour with Different Fracture Mechanic Concepts on Example of Unoriented and Cold-Rolled Polypropylene. J. Appl. Polym. Sci. 66 (1997) pp. 1237-1249
• 7. Grellmann, W.: In: Schmiedel, H. (Hrsg.): Handbuch der Kunststoffprüfung. Carl Hanser Verlag München Wien (1992), S. 145/146 und 175
• 8. Sumpter, J. G. D.; Turner, C. E.: Cracks and Fracture. ASTM STP 601 (1976) 3–18
• 9. Grellmann, W.: In: Grellmann, W., Seidler. S. (Hrsg.): Kunststoffprüfung. Carl Hanser Verlag München Wien (2005) 1. Auflage S. 79
• 10. Grellmann, W., Che, M.: Assessment of Temperature-Dependent Fracture Behaviour with Different Fracture Mechanic Concepts on Example of Unoriented and Cold-Rolled Polypropylene. J. Appl. Polymer Science, 66 (1997) pp. 1237–1249