Biegemodul

Ein Service der
Polymer Service GmbH Merseburg
Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de
Unser Weiterbildungsangebot: https://www.psm-merseburg.de/weiterbildung
PSM bei Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg

Biegemodul

Bestimmungsmethoden

Der Biegemodul E_f wird zumeist im Dreipunkt- oder Vierpunktbiegeversuch bei quasistatischer Beanspruchung [1–3] an Kunststoffen bzw. kurzfaserverstärkten oder gefüllten Kunststoffverbunden bestimmt. Der Versuch an steifen und halbsteifen Kunststoffen, d. h. thermoplastischen Formmassen oder Extrudier- und Gussmassen, wird entsprechend der Norm DIN EN ISO 178 [2] im Dreipunktbiegeversuch durchgeführt. Für faserverstärkte Kunststoffe kann der Dreipunkt- oder Vierpunktbiegeversuch (Verfahren A oder B) nach der DIN EN ISO 14125 [3] genutzt werden. Der Biegemodul kann allerdings auch bei dynamischer Belastung als komplexer Modul ermittelt werden (siehe: Dynamisch-Mechanische Analyse (DMA) – Biegebeanspruchung).

Definition des Biegemoduls

Die Ermittlung des Elastizitätsmoduls bei einer quasistatischen Biegebeanspruchung unterscheidet sich in der Kunststoffprüfung prinzipiell nicht von anderen mechanischen Beanspruchungen, wie z. B. im Zugversuch oder Druckversuch. Der E-Modul wird im linear elastischen und linear-viskoelastischen Deformationsbereich als Sekantenmodul zwischen 0,05 und 0,25 % Randfaserdehnung ermittelt (siehe auch: Elastizitätsmodul Beispiele Kennwertermittlung), wobei die Prüfgeschwindigkeit identisch mit der des eigentlichen Biegeversuchs sein kann (Bild 1). In Analogie zum Zugversuch können für die Bestimmung des E-Moduls und der Biegeeigenschaften jedoch auch unterschiedliche Prüfgeschwindigkeiten verwendet werden, wobei der Umschaltpunkt der Prüfgeschwindigkeiten dann oberhalb von 0,25 % Randfaserdehnung liegen muss. Die allgemeine Berechnung der Biegemoduls E_f wird nach der Gl. (1) vorgenommen, allerdings sind im konkreten messtechnischen Fall die geometrischen Bedingungen und der Messort zu beachten.

$E_{f}={\frac {\sigma _{f2}-\sigma _{f1}}{\varepsilon _{f2}-\varepsilon _{f1}}}={\frac {\Delta \sigma _{f}}{\Delta \varepsilon _{f}}}={\frac {\Delta \sigma _{f}}{0,002}}$

(1)

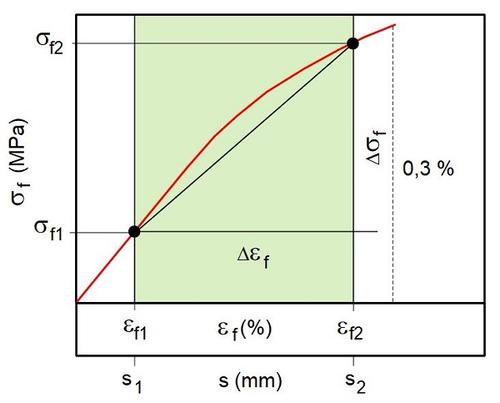
Bild 1:

Ermittlung des Sekantenmoduls im Drei- und Vierpunktbiegeversuch

Messtechnische Ermittlung des Biegemoduls

Zur Ermittlung des Biegemoduls E_f werden in der quasistatischen Kunststoffprüfung bei Biegebeanspruchung der Dreipunkt- oder Vierpunktbiegeversuch unter Nutzung einer Universalprüfmaschine angewandt. Bei Anwendung der Norm DIN EN ISO 178 ist nur der Dreipunktbiegeversuch vorgesehen, wobei hier in der Regel die Messung der Mittendurchbiegung angewandt wird. Im Fall des Biegeversuch kann die Traversenwegmessung (Bild 2a) zur Bestimmung der Mittendurchbiegung (Gl. 2) benutzt werden, wogegen bei der Ermittlung des Biegemoduls ein mittig positionierter Dehnmessfühler verwendet werden muss (Bild 2b). In dieser Gleichung ist I_y das minimale axiale Flächenträgheitsmoment (siehe Biegeversuch) des prismatischen Prüfkörpers.

$s={\frac {F\cdot L^{3}}{48\cdot E_{f}\cdot I_{y}}}$

(2)

Da der Bezugspunkt der Durchbiegungsmessung sowohl bei der Traversenwegmessung (siehe auch: Zugversuch und Druckversuch) oder bei Anwendung eines Mittensensors identisch ist (Widerlager der Biegefinnen), ist die Berechnungsgleichung (3) für beide messtechnischen Fälle gleich.

$E_{f}={\frac {F\cdot L^{3}}{s\cdot 4b\cdot h^{3}}}$

(3)

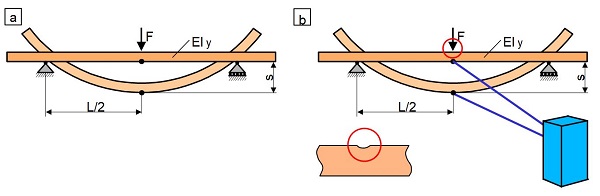
Bild 2:

Ermittlung des Biegemoduls im Dreipunktbiegeversuch: (a) mittels Traversenwegmessung und (b) mit einem Dehnmessfühler

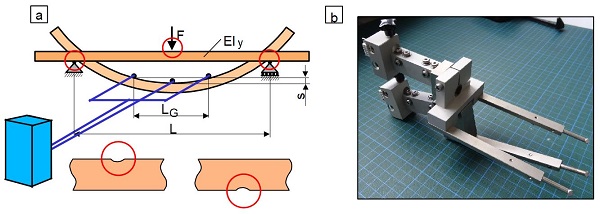
Der Vorteil des Dehnmessfühlers ist in der Tatsache begründet, dass das Eindringen der Biegefinne in die Oberfläche des Prüfkörpers nicht erfasst wird, wodurch der Biegemodul im Vergleich zur Traversenwegmessung etwas größer ist (bis ca. 10 %). Von der Fa. ZwickRoell GmbH & Co. KG, Ulm, als auch Instron Deutschland GmbH, Pfungstadt, werden derartige Biegefühler kommerziell angeboten (Bild 3). In Verbindung mit dem Aufnehmer Multisens der Fa. ZwickRoell werden zusätzlich zu den Dehnmessfühlern für Zugversuche (siehe: Zugversuch, Wegmesstechnik) auch Adapter zur Nutzung für Druckversuche als auch für Biegeversuche angeboten. Der mittige Fühler kann dabei für die Messung des Druckmoduls, aber auch für die Erfassung der Mittendurchbiegung zur Bestimmung des Biegemoduls im Drei- und Vierpunktbiegeversuch verwendet werden (siehe Bild 2b). Soll das Eindringen der Widerlager im Biegeversuch nicht im Messsignal erfasst werden, dann können alternativ sogenannte Gabelfühler angewandt werden, die ein Differenzmesssignal zwischen den Gabeln und dem Mittelfühler erzeugen. Aufgrund dessen, dass dieses Messsignal wesentlich kleiner als z. B. der Traversenweg ist, müssen hier hochauflösende Messtechniken benutzt werden (Bild 4).

Bild 3:

Dehnmessfühler für die Mittendurchbiegung (a) Deflectometer W-E401-H der Fa. Instron Deutschland GmbH, Pfungstadt, und (b) Biegesensor BTC-EXOMFL.H01 der Fa. ZwickRoell GmbH & Co. KG, Ulm

Bild 4:

Anwendung von (a) Gabelfühlern im Dreipunktbiegeversuch und (b) Gabelfühler für den Multisens-Aufnehmer der Fa. ZwickRoell GmbH & Co. KG, Ulm

Die Mittendurchbiegung hängt hierbei von den geometrischen Abmessungen des Gabelfühlers ab und berechnet sich nach Gl. (4). Die Berechnung des Biegemoduls unter Verwendung von Gabelfühlern, die oft nicht in der Prüfsoftware des Prüfmaschinenherstellers enthalten ist, kann nach Gl. (5) mittels externer Software programmiert und ausgewertet werden.

$s={\frac {F\cdot L_{G}^{2}}{96\cdot E_{f}\cdot I_{y}}}\cdot (3L-L_{G})$

(4)

$E_{f}={\frac {F\cdot L_{G}^{2}(3L-L_{G})}{s\cdot 8b\cdot h^{3}}}$

(5)

Bei der Ermittlung des Biegemoduls im Vierpunktbiegeversuch existieren verschiedene messtechnische Varianten, die unterschiedliche Ansprüche an die Messtechnik stellen. Die einfachsten Möglichkeiten bieten auch hier die Nutzung des Traversenwegs (Bild 5a) und die Messung der Mittendurchbiegung in Analogie zum Dreipunktbiegeversuch (Bild 5b).

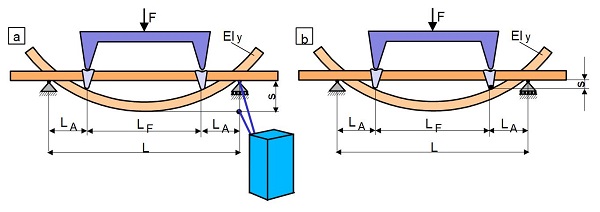
Bild 5:

Anwendung von (a) Mittendurchbiegung im Vierpunktbiegeversuch und (b) Traversenwegmessung

hertz

Aus der Mittendurchbiegung s (Bild 5a) erhält man im Fall der Vierpunktbiegung aus der Relativbewegung zwischen der Widerlagern (siehe: Auflagerabstand) und einem mittig angebrachten Dehnmessfühler den Biegemodul nach der Gl. (6).

$E_{f}={\frac {F\cdot L_{A}}{s\cdot 4b\cdot h^{3}}}\left[4L_{A}(3L_{F}+2L_{A})+3L_{F}^{2}\right]$

(6)

Mit dem Traversenweg s (Bild 5b) ergibt sich im Fall der Vierpunktbiegung der Biegemodul als Wegdifferenz zwischen dem festen Biegebalken und den Widerlagern entsprechend Gl. (7).

$E_{f}={\frac {F\cdot L_{A}^{2}}{s\cdot b\cdot h^{3}}}\left(3L_{F}+2L_{A}\right)$

(7)

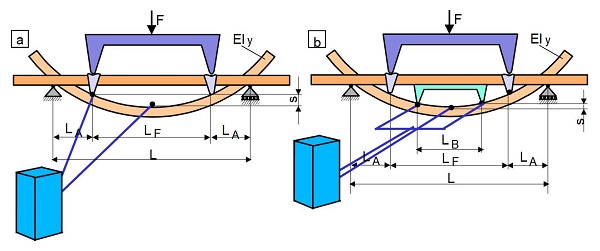
Bild 6:

Anwendung von (a) Gabelfühlern im Dreipunktbiegeversuch und (b) Gabelfühler Multisens der Fa. ZwickRoell

Der Biegemodul wird hier aus dem Differenzweg s zwischen der Mitte des Bezugs- oder Biegebalkens und der Traversenbewegung nach Bild 6a mit Gl. (8) berechnet, wodurch Einflüsse auf die Durchbiegung infolge der HERTZ’schen Pressung und des Eindringens an den Widerlagern vermieden werden.

$E_{f}={\frac {3F\cdot L_{F}^{2}\cdot L_{A}}{s\cdot 4b\cdot h^{3}}}$

(8)

Der Relativweg s zwischen der Mitte des Bezugsbalkensystems oder lose aufliegenden Gabelfühlern und der Mitte des Prüfkörpers innerhalb des Biegebalkens ergibt den Biegemodul nach Bild 6b und Gl. (9). Mit einem derartigen Messsystem können Einflüsse auf die Durchbiegung infolge Pressung an den Widerlagern und dem Prüfstempel vermieden werden, wofür allerdings ein hoch auflösendes Messsystem erforderlich ist.

$E_{f}={\frac {3F\cdot L_{B}^{2}\cdot L_{A}}{s\cdot 4b\cdot h^{3}}}$

(9)

Kennwerte des Dreipunktbiegeversuchs

Eine umfassende Literaturanalyse zu Biegemoduli und Biegefestigkeiten für zahlreiche Kunststoffe ist in [4] enthalten, von denen für ausgewählte Werkstoffe die Kennwerte in der Tabelle 1 dargestellt sind. Aufgrund der Bedeutung der Werkstoffe wurden nur unverstärkte und mit 30 M.-% Füll- oder Verstärkungsgehalt versehene Kunststoffe in dieser Aufstellung berücksichtigt, wobei diese in der Regel mittels Traversenwegmessung und bei Raumtemperatur bestimmt wurden.

Tabelle 1: Kennwerte des Biegeversuchs von technischen Kunststoffen nach [4]

Werkstoffgruppe	Modifikation	Ef (MPa)	σfM (MPa)
ABS		1373 – 3792	47,1 – 95,1
	ABS + 30 M.-% GF	6067 – 9400	86,9 – 162
	ABS + 30 M.-% CF	16547	179
	ABS / PBT + 30 M.-% GF	8205 – 10100	147 – 186
	ABS / PC + 30 M.-% GF	7505 – 8136	137 – 167
ASA		1344 – 3000	38,6 – 84,8
PA 11	PA 11	300 – 1241	51,7 – 75,8
PA 12		345 – 2068	20,0 – 98,6
	PA 12 + 30 M.-% GF	5516 – 7100	150 – 185
PA 612		1724 – 2758	82,7 – 96,5
PA 6	PA 6 (normfeucht)	380 – 1400	75,8 – 127
	PA 6 + 30 M.-% GF (normfeucht)	2600 – 5600	192 – 200
	PA 6 + 30 M.-% GB (normfeucht)	1400 – 4482	100 – 138
	PA 6 + 30 M.-% MF (normfeucht)	4000 – 5396	98,1 – 124
	PA 6 + 30 M.-% CF (normfeucht)	14000 – 17237	310
PAEK		17000	130
PBI		6500	220
PBT		1900 – 2760	62,1 – 101
	PBT + 30 M.-% GF	6343 – 11500	150 – 225
	PBT + 30 M.-% MF	3500 – 4500	90,0 – 110
PC		1889 – 2786	71,7 – 114
	PC + 30 M.-% GF	6180 – 8900	147 – 220
	PC + 30 M.-% CF	15900 – 16200	207 – 241
PE-HD		689 – 1655	25,5 – 32,4
PE-LD		69,0 – 621	7,0 – 15,2
PE-LLD		207 – 827	-
PE-MD		345 – 900	-
PE-UHMW		276 – 923	41,4
PEEK		2758 – 4300	103 – 170
	PEEK + 30 M.-% GF	8963 – 12000	221 – 261
PEI		2900 – 3447	89,6 – 165
PEK		4200 - 6205	207
PET		1090 – 2758	79,3 – 82,7
	PET + 30 M.-% GF	6965 – 11928	123 – 240
PMMA		1200 – 3654	46,2 – 121
	PMMA + 30 M.-% GF	6481	106
POM		1471 – 3150	52,0 – 95,1
	POM + 30 M.-% GF	6890 – 9000	121
	POM + 30 M.-% GB	1900 – 3170	62,1
PP		1500 – 2462	-
	PP + 30 M.-% GF	4975 – 7001	136 – 157
	PP + 30 M.-% T	2340 – 3900	38,6 – 55,2
	PP + 30 M.-% MF	2300 – 3700	40,2 – 54,9
	PP + 30 M.-% GB	1290 – 1600	-
	PP + 30 M.-% CaCO3	1896 – 2800	32,4 – 45,0
PS		1724 – 3447	37,9 – 75,8
PVC		1810 – 3378	33,0 – 93,1
	PVC + 30 M.-% GF	7930 – 9310	145 – 159
PVDF		413 – 3309	48,3 – 94,1
	PVDF + 30 M.-% GF	6300	85,0
SAN		3447 – 3792	103 – 135
TPC		196 – 3330	66,2 – 71,7
TPO		83,0 – 1569	15,2 – 43,4
TPU		345 – 750	9,0 – 14,5
	TPU + 30 M.-% GF	2175	15,2
TPZ		689	6,2

GF: Glasfasern, GB: Glaskugeln, MF: Mineralfasern, MX: nicht spezifizierte Mineralfüllung, GX: nicht spezifizierte Glasfüllung

Literaturhinweise

[1]	Bierögel, C.: Biegeversuch an Kunststoffen. In: Grellmann, W., Seidler, S. (Hrsg.): Kunststoffprüfung. Carl Hanser Verlag, München (2015) 3. Auflage, S. 147–158 (ISBN 978-3-446-44350-1; siehe AMK-Büchersammlung unter A 18)
[2]	DIN EN ISO 178 (2017-06): Kunststoffe – Bestimmung der Biegeeigenschaften (Normentwurf)
[3]	DIN EN ISO 14125 (2011-05): Faserverstärkte Kunststoffe – Bestimmung der Biegeeigenschaften
[4]	Bierögel, C., Grellmann, W.: Bend Loading. In: Grellmann, W., Seidler, S.: Mechanical and Thermomechanical Properties of Polymers. Landolt-Börnstein. Volume VIII/6A3, Springer-Verlag, Berlin (2014) S. 164–191, (ISBN 978-3-642-55165-9; siehe AMK-Büchersammlung unter A 16)