Dynamisch-Mechanische Analyse (DMA) – Biegebeanspruchung

Ein Service der
Polymer Service GmbH Merseburg
Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de
Unser Weiterbildungsangebot: https://www.psm-merseburg.de/weiterbildung
PSM bei Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg

Dynamisch-Mechanische Analyse (DMA) – Biegebeanspruchung
siehe auch:
Dynamisch-Mechanische Analyse (DMA) – Grundlagen
Dynamisch-Mechanische Analyse (DMA) – Zugbeanspruchung
Dynamisch-Mechanische Analyse (DMA) – Torsionsbeanspruchung

Grundlagen

Bei der dynamisch-mechanischen Analyse unter Biegebeanspruchung wird der genutzte Prüfkörper einer periodisch wechselnden Beanspruchung ausgesetzt, wobei durch die Variation der Frequenz der erzwungenen resonanten Schwingung die Charakterisierung der Zeitabhängigkeit des Werkstoffverhaltens möglich ist (DMA). Wird zusätzlich eine Temperierkammer verwendet, dann kann gleichzeitig die Temperaturabhängigkeit der untersuchten Eigenschaften für die betreffenden Kunststoffe erfasst und dargestellt werden (DMTA).

Durchführung der DMA unter Biegebeanspruchung

Die DMA bzw. die DMTA unter Biegebeanspruchung zählt zu den dynamisch-mechanischen Prüfverfahren mit resonanten Schwingungen, welches für die Charakterisierung viskoelastischer Eigenschaften und der Glastemperatur eingesetzt wird.
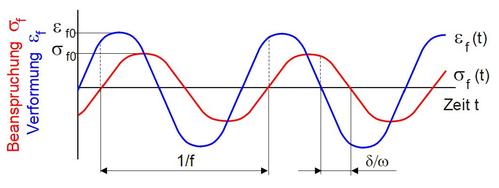
Dazu wird der Prüfkörper einer sinusförmig wechselnden mechanischen Beanspruchung veränderlicher Frequenz, wobei in der Nähe der Resonanzen eine Überhöhung der Amplituden auftritt. Bei linear-viskoelastischem Materialverhalten weisen die zeitlichen Änderungen von Spannung und Dehnung die identische Frequenz, aber unterschiedliche Phasenlagen nach den Gln. (1) und (2) auf (Bild 1).

Bild 1:

Zeitliche Änderung von Biegespannung und Randfaserdehnung bei dynamisch-mechanischer Analyse unter Verwendung erzwungener Schwingungen

$\varepsilon _{f}\left(t\right)=\varepsilon _{f0}\cdot \sin \omega t$

(1)

$\sigma _{f}\left(t\right)=\sigma _{f0}\cdot \sin \left(\omega t+\delta \right)$

(2)

Infolge der Phasenverschiebung δ zwischen Beanspruchung (Spannung) und der Verformung (Dehnung oder Scherung) ist zur Beschreibung des Spannungs-Dehnungs-Zusammenhanges der Modul als komplexe Größe E_f* nach der Gl. (3) gültig.

$E_{f}^{\ast }=E_{f}^{\prime }+iE_{f}^{\prime \prime }$

(3)

Der komplexe Modul kann als Vektor in der komplexen Zahlenebene betrachtet werden (Bild 2), dessen Richtung durch den Phasenwinkel δ und dessen Betrag durch das Verhältnis der Amplitudenwerte von applizierter erzwungenen Spannung und Dehnung gegeben ist.

Bild 2:

Darstellung des Biege-Moduls Ef* in der komplexen Zahlenebene

Der Absolutbetrag des jeweiligen Moduls ergibt sich aus dem Verhältnis der Initialbeanspruchung zur Ausgangsverformung nach der Gl. (4).

$\left|E_{f}^{\ast }\right|={\frac {\sigma _{f0}}{\varepsilon _{f0}}}$

(4)

Unter Verwendung einfacher trigonometrischer Beziehungen ist dann eine Aufteilung in den Realteil E_f‘ und den Imaginärteil E_f‘‘, die mit den Gln. (5) und (6) vorgenommen wird. Der Realteil E_f‘ wird als Speichermodul bezeichnet und ist ein Maß für die während einer Schwingungsperiode gespeicherte reversible Energie W_rev. Der Imaginäranteil E_f‘‘ erfasst die in der jeweiligen Periode dissipierte Energie W_irrev und wird als Verlustmodul benannt. Aus dem Verhältnis von Verlust- und Speichermodul ergibt sich der Verlustfaktor d = tan δ, welcher das Dämpfungsverhalten des Werkstoffs nach Gl. (7) beschreibt. Der Wert δ ist dabei der sogenannte Phasenwinkel, der Werte zwischen 0 und π/2 annehmen kann [1].

$E_{f}^{\prime }=E_{f}^{\ast }\cdot \cos \delta ={\frac {\sigma _{f0}}{\varepsilon _{f0}}}\cdot \cos \delta$

(5)

$E_{f}^{\prime \prime }=E_{f}^{\ast }\cdot \sin \delta ={\frac {\sigma _{f0}}{\varepsilon _{f0}}}\cdot \sin \delta$

(6)

$\tan \delta ={\frac {E_{f}^{\prime \prime }}{E_{f}^{\prime }}}={\frac {1}{2\pi }}\cdot {\frac {W_{irrev}}{W_{rev}}}$

(7)

Regt man einen Prüfkörper im Biegeschwingversuche nach DIN EN ISO 6721-3 [2] mit erzwungenen Resonanzschwingungen an, dann treten je nach verwendeter Einspannung und Prüfkörpergeometrie typische Prüfkörperresonanzen auf, die mit der Wellenlänge korrespondieren. Erfolgt die Anregung im Resonanzgebiet mit einer konstanten Kraftamplitude, so durchläuft die Amplitude der Auslenkung ein Maximum (Bild 3), wobei die jeweilige Resonanzfrequenz f_i und deren Halbwertsbreite Δf_i mit den viskoelastischen Eigenschaften des untersuchten Werkstoffs im Zusammenhang stehen.

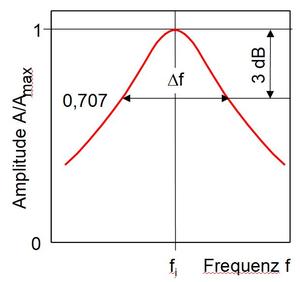
Bild 3:

Schematische Resonanzkurve eines viskoelastischen Werkstoffs

Als Prüfkörper werden prismatischer Stäbe verwendet, die entweder einseitig eingespannt sind (Verfahren A) oder an Textilfäden in den Schwingungsknoten aufgehängt werden (Verfahren B) [2] (Bild 4). Die Anregung und Registrierung der Biegeschwingungen erfolgt berührungsfrei über induktive oder kapazitive Wandler, die über dünne, auf der Prüfkörperoberfläche des Kunststoffes aufgeklebte Metallplättchen.

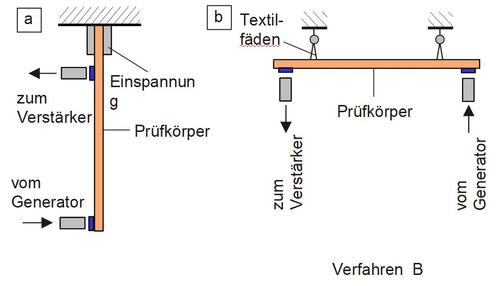
Bild 4:

Prüfanordnung zur Ermittlung viskoelastischer Eigenschaften mit erzwungenen Schwingungen im Resonanzbereich (a) mit fest dreistäbiger Einspannung und (b) freier Aufhängung des Prüfkörpers

Die Differentialgleichung (8) der Biegeschwingung kann mittels des BERNOULLI-Ansatzes nach Gl. (9) gelöst werden, wodurch die Orts- und Zeitfunktion der Schwingung Gln. (10) und (11) entstehen.

$E_{f}l_{y}\cdot {\frac {\partial ^{4}w}{\partial t^{4}}}-F{\frac {\partial ^{2}w}{\partial x^{2}}}+\rho \cdot A{\frac {\partial ^{2}w}{\partial t^{2}}}+k{\frac {\partial w}{\partial t}}=p\left(x,t\right)$

(8)

$w(x,t)=X(x)T(t)\!$

(9)

$X^{(4)}(x)-{\frac {F}{E_{f}l_{y}}}){X}^{\prime \prime }(x)-{\frac {\beta _{i}^{4}}{L^{4}}}X(x)=0$

(10)

${\ddot {T}}(t)+{\frac {k}{\rho A}}{\dot {T}}(t)+\omega ^{2}T(t)=p(x,t)$

(11)

mit:	Efly	–	Biegesteifigkeit
	L	–	Prüfkörperlänge
	A	–	Prüfkörperquerschnitt
	F	–	Prüfkraft
	ρ	–	Prüfkörperdichte
	k	–	Prüfkörperdämpfung
	w	–	Prüfkörperdurchbiegung
	x	–	Amplitude
	ω	–	Kreisfrequenz
	βi	–	i-ter Eigenwert

Aus der Lösung des Eigenwertproblems nach Gl. (10) erhält man die Eigenwertgleichung der Differentialgleichung für die Resonanzfrequenzen nach Gl. (12) für die unterschiedlichen Lagerungsfälle des Prüfkörpers β_i², die in der Tabelle 1 dargestellt sind.

${\frac {\rho A}{E_{f}l_{y}}}\cdot \omega ^{2}={\frac {\beta _{i}^{4}}{L^{4}}}$

(12)

Tabelle 1: Eigenwerte zur Bestimmung des Speichermoduls

Ordnungszahl i	einseitig eingespannt (Verfahren A)	frei aufgehängt (Verfahren B)
1	3,52	22,4
2	22,0	61,7
>2	(2i - 1)·π/2	(2i + 1)·π/2

Mit Hilfe eines Frequenzgenerators kann die Anregungsfrequenz f in einem Bereich von etwa 10¹ Hz bis 10³ Hz kontinuierlich variiert werden. Beim Durchlaufen dieses Frequenzbereiches werden am Detektor mehrere Maxima der Schwingungsamplitude registriert, die den Resonanzstellen unterschiedlicher Ordnung i (i = 1, 2, 3, …) entsprechen, wobei die Resonanzamplitude mit zunehmender Ordnungszahl immer kleiner wird, da die Dämpfung ansteigt. Aus der Resonanzfrequenz f_i der i-ten Resonanzstelle, der Dichte ρ des untersuchten Werkstoffs und den Abmessungen (freie Länge L und Dicke h) kann der Realteil (Speichermodul des komplexen Elastizitätsmoduls) nach Gl. (13) ermittelt werden.

$E^{\prime }=48\pi ^{2}\cdot \rho {\frac {L^{4}}{h^{2}}}\left[{\frac {f_{i}}{\beta _{i}^{2}}}\right]^{2}$

(13)

Aus der Halbwertsbreite der Resonanzkurve Δf_i und der Resonanzfrequenz f_i kann nach der Gl. (14) als weitere Kenngröße der Verlustfaktor tan δ und nach Gl. (15) der Verlustmodul berechnet werden, falls der Verlustfaktor des Werkstoffe ≤ 0,1 ist.

$\tan \delta ={\frac {\Delta f_{i}}{f_{i}}}$

(14)

$E^{\prime \prime }=E^{\prime }\cdot \tan \delta$

(15)

Bei Werkstoffen mit geringer Eigendämpfung (tan δ < 0,01) sollte die Analyse frei abklingender Schwingungen nach Abschalten des Erregers bei Resonanzfrequenz genutzt werden. Dabei entsteht eine Abnahme der Amplituden aufeinanderfolgender Schwingungen, aus der sich mit dem logarithmischen Dekrement Λ der Verlustfaktor ebenfalls bestimmen lässt (siehe Gl. (16)).

$\tan \delta ={\frac {\Lambda }{\pi }}={\frac {1}{\pi }}\ln {\frac {A_{n-1}}{A_{n}}}$

(16)

Ein entscheidender Nachteil des Verfahrens besteht darin, dass zur Auswertung oft nur relativ wenige Resonanzstellen zur Verfügung stehen und dass eine Beeinflussung der Lage der Resonanzstellen nur über die Veränderung der Prüfkörperabmessungen möglich ist. Bei temperaturabhängigen Messungen finden Veränderungen der Resonanzfrequenzen statt, so dass eine Ermittlung von Kennwerten bei konstanter Frequenz nicht möglich ist.

Gerätesysteme zur Durchführung der DMA

Bei der dynamisch-mechanischen Analyse oder Spektroskopie mittels Biegebeanspruchung werden meistens Tischprüfsysteme (Stand Alone Systeme) für kleinere Prüfkräfte verwendet werden. Gemeinsam ist allen Geräten, dass die Deformation des Prüfkörpers sehr klein ist und den linear-viskoelastischen Bereich nicht überschreiten sollte. Durch den Frequenzgenerator kann ein automatischer Frequenzdurchlauf erzeugt werden (Bild 5), der den Prüfkörper im Messstativ zu Schwingungen anregt. Die bei definierten Frequenzen entstehenden Amplitudenüberhöhungen können durch einen Schwingungsanalysator registriert und ausgewertet werden, wobei auch Informationen zur Dämpfungen und den Schwingungsmoden erhalten werden.

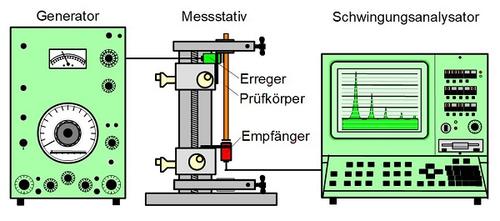
Bild 5:

Schematischer Aufbau eines DMA-System der Fa. Brüel&Kjaer, Dänemark

Literaturhinweise

[1]	Lüpke, T.: Grundlagen mechanischen Verhaltens. In: Grellmann, W., Seidler, S. (Hrsg.): Kunststoffprüfung. Carl Hanser Verlag, München (2015) 3. Auflage S. 91/92, (ISBN 978-3-446-44350-1; siehe AMK-Büchersammlung unter A 18)
[2]	DIN EN ISO 6721-3 (1996-12): Kunststoffe – Bestimmung dynamisch-mechanischer Eigenschaften – Teil 3: Biegeschwingung; Resonanzkurven-Verfahren