Instrumentierter Kerbschlagzugversuch, Beispiele

Ein Service der
Polymer Service GmbH Merseburg
Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de
Unser Weiterbildungsangebot: https://www.psm-merseburg.de/weiterbildung
PSM bei Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg

Instrumentierter Kerbschlagzugversuch, Beispiele

Allgemeines

Der instrumentierte Kerbschlagversuch (IKZV) wird bei Kunststoffen und Elastomeren zur Ermittlung bzw. Optimierung der Zähigkeit eingesetzt [1, 2]. Diese in der Literatur relativ selten beschriebene Methode der Kunststoffprüfung und Diagnostik kann jedoch vorteilhaft bei Prüfkörpern mit geringer Dicke, z. B. nach Ausarbeitung aus dünnwandigen Kunststoffbauteilen, insbesondere aber Kunststofffolien angewendet werden. Die Aussagefähigkeit der Methode und die experimentelle Durchführung des Verfahrens [3] wurde unter „Instrumentierter Kerbschlagzugversuch“ ausführlich erläutert.

In den nachfolgenden Beispielen wird die Eignung des IKZV zur Untersuchung des Einflusses von technologischen Herstellungsparametern (z. B. der Walzzeit) und Rezepturoptimierung (z. B. Gehalt von Schwefel und Ruß in Elastomeren) aufgezeigt.

Beispiel 1: Einfluss von Herstellungsbedingungen bei der Zähigkeitsoptimierung von Polyvinylchlorid

Von Hoffmann und Leps [4] wurde im Rahmen von Untersuchungen zur Zähigkeitsoptimierung von mit der Walz-Press-Technologie hergestellten schlagzähen PVC-Werkstoffen die Abhängigkeit von dem technologischen Parameter „Walzzeit“ mit Hilfe des IKZV bewertet (Bild 1). Zur Beurteilung der Zähigkeit wurde bei den bruchmechanischen Prüfungen als Kennwert die Bruchzähigkeit (siehe: Bruchmechanik) herangezogen (Gln. (1) und (2)):

Bruchzähigkeit K_Id

$K_{Id}={\frac {F_{max}}{B\cdot W^{\frac {1}{2}}}}\cdot f\left({\frac {a}{W}}\right)$

(1)

mit:

$f\left({\frac {a}{W}}\right)={\frac {\sqrt {\frac {\pi a}{2W}}}{\sqrt {1-{\frac {a}{W}}}}}\left[1,122-0,561\left({\frac {a}{W}}\right)-0,205\left({\frac {a}{W}}\right)^{2}+0,471\left({\frac {a}{W}}\right)^{3}+0,190\left({\frac {a}{W}}\right)^{4}\right]$

(2)

nach [5].

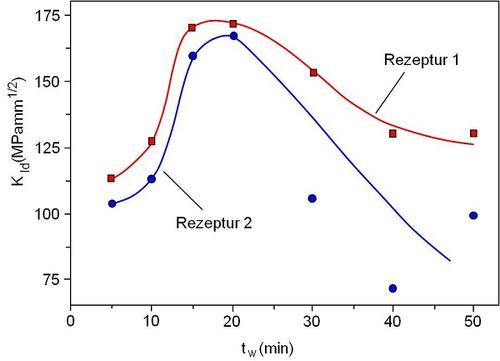
Die beiden schlagzähen PVC-Werkstoffe bestehen jeweils aus 92 Teilen PVC und 8 Teilen Modifikator (EVA-Copolymerisat mit 14 M.-% VAC), wobei das PVC der Rezeptur 1 mit K = 63 den höheren K-Wert (Kennwert für die Viskosität gegenüber der Rezeptur 2 (K = 60) aufweist. Die Walztemperatur T_W betrug 170 °C.

Bild 1:

Zähigkeitsoptimierung von zwei schlagzähen PVC-Werkstoffen – Einfluss der Walzzeit tW der Walz-Press-Technologie auf die Bruchzähigkeit KId bei einer Walztemperatur von TW = 170 °C

Für die dynamische Bruchzähigkeit K_Id wurde für beide Rezepturen der schlagzähen PVC-Werkstoffe ein Maximum der Zähigkeit bei Walzzeiten von 15 bis 20 min ermittelt, das auf einer gleichsinnigen Zu- und Abnahme sowohl der maximalen Bruchkraft F_max als auch der Bruchzeit t_B beruht, wodurch auch eine Auswertung mit dem Konzept der linear-elastischen Bruchmechanik zulässig ist.
Die höheren Zähigkeitswerte der Rezeptur 1 bei größeren Walzzeiten werden bei den Morphologiebetrachtungen in [4] auf die teilweise Erhaltung der für gutes Zähigkeitsverhalten typischen Netzwerkstruktur (PVC-Globulargerüst vom Kautschuknetzwerk durchdrungen) zurückgeführt, wie im Bild 2 an einem Beispiel gezeigt wird.

Bild 2:

Transmissionselektronenmikroskopische Aufnahme eines kontrastierten Ultradünnschnitts von PVC-P, Rezeptur 1 bei einer Walzzeit von tW = 15 min

Beispiel 2: Rezepturoptimierung von Styren-Butadien-Kautschuk (SBR)-Vulkanisaten hinsichtlich der Zähigkeitseigenschaften

Von Reincke [6‒10] wurden im Rahmen von Untersuchungen zum Zusammenhang zwischen Mischrezepturen, Struktur und bruchmechanischen Eigenschaften elastomerer Werkstoffe die Anwendungsmöglichkeiten des IKZV wesentlich erweitert. Zur Bewertung der Zähigkeit wurde bei der bruchmechanischen Prüfung als Kennwert der J_Id-Wert, ermittelt nach dem J-Integral-Konzept herangezogen (Gl. (3) bzw. Gl. (4)):

J-Werte J_Id

$J_{Id}={\frac {\eta \cdot A_{max}}{B(W-a)}}$

(3)

bzw. beim Auftreten der Rissausbreitungsenergie A_p:

$J_{Id}={\frac {\eta \cdot \left(A_{max}+A_{p}\right)}{B(W-a)}}$

(4)

Als Beispiel werden Untersuchungen an ungefüllten und gefüllten Styren-Butadien-Kautschuk (SBR)-Vulkanisaten dargestellt [6, 9, 10].
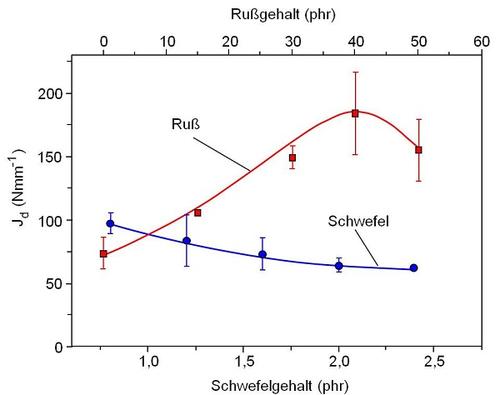
Die Vernetzung erfolgte mit Schwefel. Durch die Änderung des Gehaltes an Schwefel als Vernetzungsmittel ist es möglich, die Netzkettendichte des bei der Vulkanisation entstehenden Netzwerkes zu variieren und so die Eigenschaften des Elastomers zu beeinflussen. Bei den gefüllten SBR-Vulkanisaten handelt es sich um Vulkanisate mit gleichem Schwefelanteil und unterschiedlichen Anteilen des Füllstoffs Ruß. In Bild 3 sind die J-Werte als Widerstand gegen instabile Rissausbreitung dargestellt.

Bild 3:

Einfluss von Ruß- und Schwefelgehalt auf die J-Werte von Elastomerwerkstoffen, ermittelt im instrumentierten Kerbschlagzugversuch

Für die ungefüllten Vulkanisate zeigen die ermittelten J-Werte eine konstante Abnahme der Zähigkeit. Für die gefüllten Vulkanisate ergibt sich ein Maximum. Dieses Maximum [11‒13] weist darauf hin, dass die Füllstoffzugabe nur bis 40 phr Ruß zur Verbesserung der Zähigkeitseigenschaften des betrachteten Werkstoffsystems unter den gegebenen Versuchsbedingungen führt.

Literaturhinweise

[1]	Grellmann, W., Seidler, S. (Hrsg.): Kunststoffprüfung. Carl Hanser Verlag, München (2015) 3. Auflage, S. 293‒297 (ISBN 978-3-446-44350-1; siehe AMK-Büchersammlung unter A 18)
[2]	Reincke, K.: Bruchmechanische Bewertung von gefüllten und ungefüllten Elastomerwerkstoffe. Mensch & Buch Verlag, Berlin (2005), (ISBN 978-3-86664-021-4; siehe AMK-Büchersammlung unter B 1-13)
[3]	MPK-Prozedur MPK-IKZV (2017-07): Prüfung von Kunststoffen – Instrumentierter Kerbschlagzugversuch
[4]	Hoffmann, H., Leps, G., Grellmann, W., Stephan, R., Hanisch, H.: Beurteilung der Zähigkeitseigenschaften von schlagzähem PVC. Plaste und Kautschuk 32 (1985) 379‒381
[5]	Anderson T. L.: Fracture Mechanics. Fundamentals and Applications. 3rd Ed., CRC Press Boca Raton (2005)
[6]	Reincke, K.: Elastomere Werkstoffe – Zusammenhang zwischen Mischungsrezeptur, Struktur und mechanischen Eigenschaften sowie dem Deformations- und Bruchverhalten, Habilitation, Martin-Luther-Universität Halle-Wittenberg, Shaker Verlag (2016) (ISBN 978-3-8440-4637-3; siehe AMK-Büchersammlung unter B 2-2)
[7]	Reincke, K., Grellmann, W.: Elastomers. Impact Loading. In: Grellmann, W., Seidler, S.: Mechanical and Thermomechanical Properties of polymers. Landolt-Börnstein. Volume VIII/6A3, Springer Verlag, Berlin (2014) S. 502‒509, (ISBN 978-3-642-55165-9; siehe AMK-Büchersammlung unter A 16)
[8]	Reincke, K., Grellmann, W.: Approaches to Characterise the Mechanical Properties of Films and Elastomers. In: Grellmann, W., Langer, B.: Deformation and Fracture Behaviour of Polymer Materials. Springer Series in Materials Science 247, Springer Verlag, Berlin Heidelberg (2017) 225‒336 (ISBN 978-3-319-41877-3; e-Book: ISBN 978-3-319-41879-7; siehe AMK-Büchersammlung unter A 19)
[9]	Grellmann, W., Reincke, K., Lach, R., Heinrich, G.: Characterization of Crack Toughness Behaviour of Unfilled and Filled Elastomers. Kautschuk, Gummi, Kunststoffe 54 (2001) 397‒402
[10]	Grellmann, W., Reincke, K.: Quality Improvement of Elastomers. Use of Instrumented Notched Tensile-impact Testing for Assessment of Toughness. Materialprüfung 46 (2004) 168‒175
[11]	Reincke, K., Grellmann, W., Heinrich, G.: Investigation of Mechanical and Fracture Mechanical Properties of Elastomers Filled with Precipitated Silica and Nanofillers Based upon Layered Silicates. Rubber Chemistry and Technology 77 (2004) 662‒677
[12]	Reincke, K., Klüppel, M., Grellmann, W.: Investigation of Fracture Mechanical Properties of Filler-reinforced Styrene-butadiene Elastomers. Kautschuk Gummi Kunststoffe 62 (2009) 246‒251
[13]	Grellmann, W., Reincke, K.: Technical Material Diagnostics – Fracture Mechanics of Filled Elastomer Blends. In: Grellmann, W., Heinrich, G., Kaliske, M. Klüppel, M., Schneider, K., Vilgis, T. (Eds.): Fracture Mechanics and Statistical Mechanics of Reinforced Elastomeric Blends. Springer, Berlin (2013) 227‒268