Bruchmodell faserverstärkte Kunststoffe
| Ein Service der |
|---|

|
| Polymer Service GmbH Merseburg |
| Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de |
| Unser Weiterbildungsangebot: https://www.psm-merseburg.de/weiterbildung |
| PSM bei Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg |
Bruchmodell faserverstärkte Kunststoffe
Modelle zur Beschreibung des mechanischen Deformations- und Rissausbreitungsverhaltens faserverstärkter Kunststoffe [1]
Theoretische Modelle zur Berechnung des mechanischen Verhaltens von Verbundwerkstoffen aus den Eigenschaften der Komponenten werden seit Beginn der Erforschung dieser Werkstoffgruppe für die Vorhersage von Verbundeigenschaften, aber auch für eine Veranschaulichung der physikalischen Zusammenhänge eingesetzt und sind für unterschiedliche Kenngrößen und Werkstoffsysteme bekannt und erprobt [2–4]. Eines der ersten Modelle von Halpin und Tsai [2] beschrieb den Elastizitätsmodul des Verbundes als Funktion des Faservolumenanteils φV und der charakteristischen Verbundkenngrößen Modulverhältnis EF/EM und Aspektverhältnis der Fasern lF/dF.
Lauke, Schultrich und Pompe [3, 5] haben ein umfangreiches Modell zur Berechnung bruchmechanischer Kenngrößen für glasfaserverstärkte Kunststoffe vorgelegt, welches erfolgreich zur Abschätzung von Kenngrößen des instabilen Risswachstums von PE- und PP-Glasfaserverbundwerkstoffen [6] und von Risswiderstandskurven von PA66-Kohlefaserverbundwerkstoffen eingesetzt wurde [7]. In beiden Fällen wurden die Modelle unter Voraussetzung eines relativen Matrixsprödbruches verwendet, welcher auch bei trockenem PA6 bei Raumtemperatur festgestellt werden kann [7]. In diesem Fall kann zum Beispiel der J-Wert; ermittelt mit Hilfe des J-Integralkonzeptes und den entsprechenden J-Integralauswertemethoden mit Gl. (1) abgeschätzt werden. Dieser Kennwert ist dabei eine Funktion des Faservolumenteils φV und der mittleren Faserlänge l. Aufgrund der Hauptversagensmechanismen Debonding, Gleiten, Pull-Out und Sprödbruch von Matrixbrücken, gehen auch die entsprechenden volumenspezifischen Energien mit in Gl. (1) ein.
| (1) |
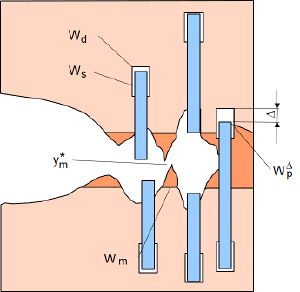
Liegt hingegen ein stark duktiles Verhalten der Polymermatrix vor, dann verändert sich das Deformationsverhalten des Verbundes und Energiedissipation findet hauptsächlich durch die in Bild 1 dargestellten Mechanismen statt. Bei kurzglasfaserverstärkten Werkstoffen tritt Faserbruch nur bedingt auf, weil die Faserlängen hier in der Regel kleiner lc sind. Die kritische Faserlänge lc ist dabei die Länge der Faser, bei der für Debonding und Gleiten mehr Energie aufgewandt werden müsste als für den Faserbruch. Energiebeiträge durch Faserbruch können daher im Allgemeinen bei kurzglasfaserverstärkten Kunststoffen vernachlässigt werden. Statt Matrixsprödbruch kommt es in der Prozesszone bei global duktilem Verhalten zu lokalen Fließvorgängen. In Abhängigkeit von den Eigenschaften des Faser-Matrix-Systems ergeben sich verschiedene mögliche Zusammensetzungen der Bruchenergie WG. Treten alle in Bild 1 dargestellten Mechanismen auf, dann ist die Bruchenergie die Summe aller bruchflächenspezifischen Energiebeiträge gemäß Gl. (2).
| (2) |
| Bild 1: | Versagensarten von Polymer-Faser-Verbunden bei duktilem Matrixbruch nach Lauke et al. [3]; Energiedissipation durch: Debonding (Wd), Gleiten (Ws), plastische Deformation der Matrixbrücken (Wm), reduziertes Pull-Out (WpΔ) und Matrixbruch |
Die Abhängigkeit der Mechanismen vom Faservolumenanteil
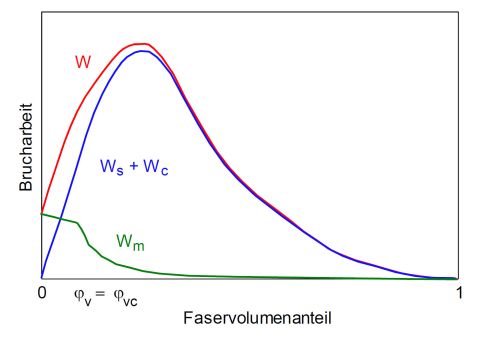
Jeder Energiedissipationsmechanismus unterliegt einer bestimmten Abhängigkeit vom Faservolumenanteil. Diese Zusammenhänge sind in Bild 2 dargestellt, wobei auch die sich ergebende Summenkurve WG enthalten ist. Die beim Risswachstum durch plastische Matrixdeformation dissipierte Energie Wm nimmt mit zunehmendem Faservolumenanteil φV ab, weil der Anteil der am Deformationsprozess beteiligten Polymermatrix mit dem Faktor (1–φV) ebenfalls sinkt [3]. Die funktionelle Abhängigkeit von Wm von φV weist eine Unstetigkeitsstelle bei φV = φVc auf. Bis zu diesem Faservolumenanteil tritt abhängig von der Prüfkörperdicke und den Beanspruchungsbedingungen makroskopisches plastisches Fließen auf. Die charakteristische Verbundkenngröße φVc ist vom Aspektverhältnis abhängig und errechnet sich aus Gl. (3). Oberhalb von φVc nimmt die dissipierte Energie für plastische Matrixdeformation exponentiell ab.
| (3) |
Die durch Debonding Wd und Gleiten Ws von Fasern in der Matrix dissipierte Energie durchläuft ein Maximum. Das wird dadurch induziert, dass bei niedrigen Verstärkungsgraden die zunehmende Anzahl der energiedissipativ aktiven Faserenden dominiert, während bei höheren Verstärkungsgraden die Länge der abgelösten und gleitenden Faserenden stärker abnimmt, als durch deren Anzahl energetisch kompensiert werden kann [3]. Die spezifischen, für die Energiedissipation durch Debonding (Ablösung der Fasern und besonders der Faserenden von der Matrix) und Sliding (Gleiten der Fasern in der Matrix) verantwortlichen, Längen ld und ls sind Funktionen des Faservolumenanteils φV. Weiterhin werden sie von Werkstoffkennwerten der Faser und der Matrix wie den E-Moduln EF und EM, den Querkontraktionszahlen von Faser νF und Matrix νM, dem Gleitreibungskoeffizienten μ sowie der physikalisch-chemisch verursachten Schubspannung τs zwischen Faser und Matrix beeinflusst. Die Länge der Faserablösung bildet sich damit im energetischen Gleichgewicht zwischen den wirkenden Spannungen entlang der Faser in der Beanspruchungsrichtung und den auftretenden Normalspannungen an der Faser-Matrix-Grenzfläche (siehe: Faser-Matrix-Haftung). Diese gehen aus unterschiedlichen Querkontraktionen von Faser und Matrix sowie Reibungs- und Haftkräften hervor.
Die Abhängigkeit der Brucharbeit vom Faservolumenanteil
Das in Bild 2 dargestellte Maximum der Brucharbeit kann auch so interpretiert werden, dass die an den Faserenden stattfindende Energiedissipation durch Debonding und Gleiten so lange zunimmt, bis der Abstand benachbarter Faserenden nicht mehr für voneinander unabhängige Deformationsvorgänge ausreicht. Generell deckt sich das mit den experimentellen Beobachtungen einer kleiner werdenden Prozesszone (siehe: Bruchprozesszone) mit steigendem Fasergehalt [8] und damit sinkenden Energiebeiträgen durch plastische Deformationsvorgänge in der Dissipationszone [9].
| Bild 2: | Brucharbeit in Abhängigkeit vom Faservolumenanteil bei dynamischer Beanspruchung (nach Lauke et al. [3]) |
Siehe auch
- Bruchverhalten
- Faserverstärkte Kunststoffe
- Faser-Matrix-Haftung
- Prüfung von Verbundwerkstoffen
- Kurzfaserverstärkte Verbundwerkstoffe
Literaturhinweise
| [1] | Kroll, M.: Hybride PA 6-Werkstoffe – Methoden der bruchmechanischen Zähigkeitscharakterisierung und Eigenschaftsprofil in Abhängigkeit von den Verarbeitungsbedingungen und der Werkstoffzusammensetzung. Dissertation, MLU Halle-Wittenberg (2013), ISBN 978-3-8440-2335-0, Shaker Verlag Aachen (siehe AMK-Büchersammlung unter B 1-25) |
| [2] | Halpin, J. C., Tsai, S. W.: Environmental Factors in Composite Materials Design. AFML TR (1967) S. 67–423 |
| [3] | Lauke, B., Schultrich, B., Pompe, W.: Theoretical Considerations of Toughness of Short-fibre Reinforced Thermoplastics. Wissenschaftliche Berichte 40, Zentralinstitut für Festkörperphysik und Werkstoffforschung, Dresden (1989) |
| [4] | Aykol, M., Isitman, N. A., Firlar, E., Kaynak, C.: Strength of Short Fiber Reinforced Polymers: Effect of Fiber Length Distribution. Polym. Compos. 29 (2008) 6, S. 644–648 |
| [5] | Lauke, B., Friedrich, K.: Fracture Toughness Modelling of Fiber Reinforced Composites by Crack Resistance Curves. Adv. Compos. Mater 2 (1992) 4, S. 261–275 |
| [6] | Seidler, S., Grellmann, W.: Zähigkeit von teilchengefüllten und kurzglasfaserverstärkten Polymerwerkstoffen. VDI-Fortschr.-Ber., VDI-Reihe 18 Nr. 92, VDI Verlag, Düsseldorf (1991) (ISBN 3-18-149218-3; siehe AMK-Büchersammlung unter A 4) |
| [7] | Langer, B.: Bruchmechanische Bewertung von Polyamid-Werkstoffen. Dissertation, Martin-Luther-Universität Halle-Wittenberg (1997), Logos Verlag; (ISBN 3-897-22063-6; siehe AMK-Büchersammlung unter B 1-5) |
| [8] | Gomina, M., Pinot, L., Moreau, R., Nakache, E.: Fracture Behaviour of Short Glass Fibre-reinforced Rubber-toughened Nylon Composites. Fracture of Polymers, Composites and Adhesives II Volume 32 (2003) S. 399–418 |
| [9] | Laura, D. M., Keskkula, H., Barlow, J. W., Paul, D. R.: Effect of Glass Fiber and Maleated Ethylene-propylene Rubber Content on the Impact Fracture Parameters of Nylon 6. Polymer 42 (2001) 14, 6161–6172 |

![{\displaystyle J_{c}={\frac {2\gamma _{m}^{0}(1-\varphi _{V})}{1-2\beta E_{c}\left[{\frac {\eta _{d}}{(\sigma _{c}^{d})^{2}}}+{\frac {\eta _{s}}{(\sigma _{c}^{s})^{2}}}\right]-{\frac {\varphi _{V}\tau _{p}l}{2\sigma _{c}^{d}d}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1570fd3d83cb9b641fbaf1746e76a83742985f61)