Bruchprozesszone

Ein Service der
Polymer Service GmbH Merseburg
Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de
Unser Weiterbildungsangebot: https://www.psm-merseburg.de/weiterbildung
PSM bei Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg

Bruchprozesszone

Allgemeines

Von Blumenauer [1] wird beschrieben, dass die Rissausbreitung durch Wechselwirkungsprozesse zwischen den Mikrorissen und der Morphologie, bei Metallen spricht man im Allg. von Gefüge, in einem rissspitzennahen Bereich bestimmt wird. In den meisten Fällen ist für die Rissausbreitung in diesem Bereich charakteristisch, dass Mikrorisse bzw. Hohlräume entstehen, die sich zu einem Hauptriss vereinigen.

Bruchprozesszone für Kunststoffe

In Kunststoffen wird die Rissentstehung durch lokale plastische Deformationen eingeleitet, wie sie bei der Bildung von Crazes oder Scherbändern auftreten. Crazes enthalten im Gegensatz zu Rissen hochorientiertes verstrecktes Material, das sich parallel zur Richtung der Beanspruchung ausbildet. Zur Bildung von Crazes kommt es, wenn an Stellen erhöhter Spannungskonzentration (Defekte im molekularen Aufbau, Fremdpartikel, Hohlräume usw.) die Fließspannung überschritten wird.

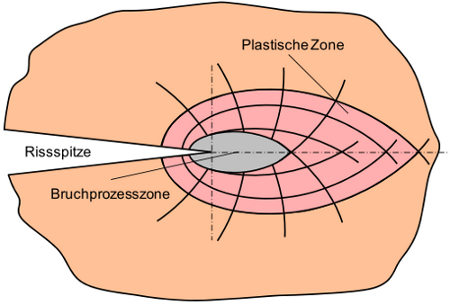
Bild 1:

Bruchprozesszone und plastische Zone an der Rissspitze [1]

Dabei können stark beanspruchte Makromoleküle aufreißen und Mikrohohlräume entstehen. Mit dem weiteren Wachstum der Crazes werden die Fibrillen zwischen den Hohlräumen zerstört und ein Riss breitet sich entlang der Crazeachse aus. Im Bild 1 sind die geometrischen Relationen zwischen der Bruchprozesszone und der plastischen Zone bildlich dargestellt.

Im Gegensatz zu den Kunststoffen wird bei spröden kristallinen Werkstoffen die Bruchprozesszone als sehr klein angenommen; häufig in der Größenordnung von nur wenigen Atomabständen [1].

Bedeutung für die Modellierung von teilchen- und faserverstärkten Kunststoffen

Eine besondere Rolle spielt die Bruchprozesszone bei der Aufstellung von Bruchmodellen für Teilchenverbunde [2, 3] oder faserverstärkte Kunststoffe [4, 5].

Zur Beschreibung des mechanischen Deformations- und Rissausbreitungsverhaltens sind die Deformationsvorgänge in sehr ausgedehnten Prozesszonen mit Mikrorissen die entscheidende Voraussetzung für eine Vorausberechnung der Zähigkeit mit Hilfe bruchmechanischer Werkstoffkenngrößen.

In diesem Zusammenhang ist besonders erwähnenswert, dass die Prozesszone dieselbe Bedeutung hat wie die von Barenblatt [6] innerhalb seines atomistischen Rissmodells (Kohäsivzonenmodell) eingeführte Kohäsivzone. Dieses Modell hat sich bei der Modellierung des Rissfortschritts in elastisch-plastischen Werkstoffen (also auch Kunststoffen), innerhalb von Kleb- und Schweißverbindungen sowie der Delamination von geschichteten Werkstoffen und Bauteilen (wie Faserverbunden und Peelfolien [8]) bewährt [7]. Das Kohäsivzonenmodell eignet sich auch sehr gut zur numerischen Behandlung von Bruchvorgängen im Rahmen der Finite-Elemente-Methode [7].

Literaturhinweise

[1]	Blumenauer, H., Pusch, G.: Technische Bruchmechanik. Deutscher Verlag für Grundstoffindustrie, Leipzig Stuttgart (1993) 3. Auflage, S. 22, (ISBN 3-342-00659-5; siehe AMK-Büchersammlung unter E 29-3)
[2]	Grellmann, W., Bohse, J., Seidler, S.: Bruchmechanische Analyse des Zähigkeitsverhaltens von teilchengefüllten Thermoplasten. Mat.-wiss. und Werkstofftechnik 21 (1990) H. 9, S. 359−364
[3]	Grellmann, W., Seidler, S., Bohse, J.: Zähigkeit und Morphologie von Thermoplast/Teilchenverbunden. Kunststoffe 81 (1991) H. 2, S. 157−162 und Toughness and Morphology of Thermoplastic / Particle Composites. Kunststoffe German Plastics 81 (1991) H. 2, S. 29−32
[4]	Grellmann, W., Lauke, B., Seidler, S.: Application of J-Integral Concept for the Description of Toughness Properties of Fiber Reinforced Polyethylene Thermoplastics. Polymer Composites October Vol. 12, (1991) No. 5, 320−326
[5]	Grellmann, W., Seidler, S., Nezbedova, E.: Analysis of Fracture Behaviour of Fibre Reinforced Polypropylene Using R-Curve Concept. Makromolekulare Chemie, Macromol. Symp. 41 (1991) 195−208
[6]	Barenblatt, G. I.: On Equilibrium Cracks Formed in Brittle Fracture. General Concepts and Hypotheses. Axisymmetric Cracks. Prikladnaya Matematika i Mekhanika 23 (1959) 434‒444 (in Russisch); Journal of Applied Mathematics and Mechanics 23 (1959) 622‒636 (englische Übersetzung)
[7]	Gross, D., Seelig, T.: Bruchmechanik. Mit einer Einführung in die Mikromechanik. 5. Auflage, Springer-Verlag, Berlin Heidelberg (2011), (ISBN 978-3-6421-0195-3), Kapitel 5.3 Kohäsivzonenmodelle, S. 156‒160
[8]	Geißler, G., Kaliske, M., Grellmann, W., Nase, M.: Peel Process Simulation of Sealed Polymeric Film – Computational Modelling of Experimental Results. Engineering Computations 24 (2007) 586‒607