Biegeversuch Schubspannung: Unterschied zwischen den Versionen

Aus Lexikon der Kunststoffprüfung
Zur Navigation springen Zur Suche springen
 
(4 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt)
Zeile 13: Zeile 13:
 
|}
 
|}
  
−
Umgekehrt kann also ein zu geringer [[Auflagerabstand]] oder nicht angepasste Auflagerradien eine unzulässig hohe Schubspannung im Querschnitt erzeugen. Dieser Spannungsanteil wird zwar in der Berechnung nicht berücksichtigt, er führt aber im Regelfall zu einer Verringerung der [[Kennwert]]e des [[Biegeversuch]]s. Das Auftreten der Schubspannung im [[Biegeversuch]] kann mit Hilfe von '''Bild 2''' veranschaulicht werden [3].
+
Umgekehrt kann also ein zu geringer [[Auflagerabstand]] oder nicht angepasste Auflagerradien eine unzulässig hohe Schubspannung im Querschnitt erzeugen. Dieser Spannungsanteil wird zwar in der Berechnung nicht berücksichtigt, er führt aber im Regelfall zu einer Verringerung der [[Kennwert]]e des [[Biegeversuch]]s. Das Auftreten der Schubspannung im [[Biegeversuch]] kann mit Hilfe von '''Bild 2''' veranschaulicht werden [3, 4].
  
 
==Enstehung und Verteilung von Schubspannungen im Biegeprüfkörper==
 
==Enstehung und Verteilung von Schubspannungen im Biegeprüfkörper==
Zeile 28: Zeile 28:
 
|}
 
|}
  
−
Die Schubspannung erreicht ihr Maximum im Bereich der neutralen Faser und weist eine parabolische Verteilungsfunktion auf ('''Bild 2'''). Zur Vermeidung unzulässiger Schubspannungseinflüsse im [[Biegeversuch]] muss nach DIN EN ISO 178 [1] ein Längen-Dicken-Verhältnis l/h = 20, bzw. ein Stützweiten-Dicken-Verhältnis von L/h = 16 eingehalten werden. Aufgrund der Schubempfindlichkeit von Laminaten beträgt in diesem Fall das Stützweiten-Dicken-Verhältnis L/h = 20 – 25. Aus dem sogenannten „Short-Beam Bend Test“, d. h. dem [[Biegeversuch]] mit engem [[Auflagerabstand]] kann man dann an Laminaten die [[Interlaminare Scherfestigkeit]] (ILSF) ermitteln [4, 5].
+
Die Schubspannung erreicht ihr Maximum im Bereich der neutralen Faser und weist eine parabolische Verteilungsfunktion auf ('''Bild 2'''). Zur Vermeidung unzulässiger Schubspannungseinflüsse im [[Biegeversuch]] muss nach DIN EN ISO 178 [1] ein Längen-Dicken-Verhältnis l/h = 20, bzw. ein Stützweiten-Dicken-Verhältnis von L/h = 16 eingehalten werden. Aufgrund der Schubempfindlichkeit von Laminaten beträgt in diesem Fall das Stützweiten-Dicken-Verhältnis L/h = 20 – 25. Aus dem sogenannten „Short-Beam Bend Test“, d. h. dem [[Biegeversuch]] mit engem [[Auflagerabstand]] kann man dann an Laminaten die [[Interlaminare Scherfestigkeit]] (ILSF) ermitteln [5, 6].
 +
 
 +
 
 +
==Siehe auch==
 +
*[[Biegeversuch]]
 +
*[[Biegeversuch Fließspannung]]
 +
*[[Biegeversuch Nachgiebigkeit]]
 +
*[[Randfaserdehnung]]
 +
*[[Elastizitätsmodul Beispiele Kennwertermittlung]]
  
  
Zeile 35: Zeile 43:
 
|-valign="top"
 
|-valign="top"
 
|[1]
 
|[1]
−
|DIN EN ISO 178 (2017-06): Kunststoffe – Bestimmung der Biegeeigenschaften (Normentwurf)
+
|DIN EN ISO 178 (2019-08): Kunststoffe – Bestimmung der Biegeeigenschaften
 
|-valign="top"
 
|-valign="top"
 
|[2]
 
|[2]
−
|DIN EN ISO 14125 (2011-05): Faserverstärkte Kunststoffe – Bestimmung der Biegeeigenschaften
+
|DIN EN ISO 14125 (2011-05): Faserverstärkte Kunststoffe – Bestimmung der Biegeeigenschaften; Technical Corrigendum Cor.1:2001 + Amd.1:2011
 
|-valign="top"
 
|-valign="top"
 
|[3]
 
|[3]
−
|[[Bierögel, Christian|Bierögel, C.]]: Biegeversuch an Kunststoffen. In: [[Grellmann,_Wolfgang|Grellmann, W.]], [[Seidler,_Sabine|Seidler, S.]] (Hrsg.): Kunststoffprüfung. Carl Hanser Verlag, München (2015) 3. Auflage, S. 147–158 (ISBN 978-3-446-44350-1; siehe [[AMK-Büchersammlung]] unter A 18)
+
|[[Bierögel, Christian|Bierögel, C.]]: Biegeversuch an Kunststoffen. In: [[Grellmann,_Wolfgang|Grellmann, W.]], [[Seidler,_Sabine|Seidler, S.]] (Hrsg.): Kunststoffprüfung. Carl Hanser Verlag, München (2024) 4. Auflage, S. 141–151 (ISBN 978-3-446-44718-9; E-Book: ISBN 978-3-446-48105-3; siehe [[AMK-Büchersammlung]] unter A 23)
 
|-valign="top"
 
|-valign="top"
−
|[4]
+
|[4]  
−
|Altstädt, V.: Prüfung von Verbundwerkstoffen. In: Grellmann, W., Seidler, S. (Hrsg.): Kunststoffprüfung. Carl Hanser Verlag, München (2011) 2. Auflage, S. 560–561 (ISBN 978-3-446-42722-8; siehe [[AMK-Büchersammlung]] unter A 12)
+
|Bierögel, C., [https://www.researchgate.net/profile/Wolfgang-Grellmann Grellmann, W.]: Bend loading. In: [https://de.wikipedia.org/wiki/Wolfgang_Grellmann Grellmann, W.], [https://de.wikipedia.org/wiki/Sabine_Seidler Prof. Sabine Seidler]: Mechanical and Thermomechanical Properties of Polymers. Landolt-Börnstein, Volume VIII/6A3, Springer Verlag, Berlin (2014) 164–191, (ISBN 978-3-642-55165-9; siehe [[AMK-Büchersammlung]] unter A 16)
 
|-valign="top"
 
|-valign="top"
 
|[5]
 
|[5]
 +
|[[Altstädt,_Volker|Altstädt, V.]]: Prüfung von Verbundwerkstoffen. In: [https://www.researchgate.net/profile/Wolfgang-Grellmann Grellmann, W.], Seidler, S. (Hrsg.): Kunststoffprüfung. Carl Hanser Verlag, München (2024) 4. Auflage, S. 549–550 (ISBN 978-3-446-44718-9; E-Book: ISBN 978-3-446-48105-3; siehe [[AMK-Büchersammlung]] unter A 23)
 +
|-valign="top"
 +
|[6]
 
|DIN EN ISO 14130 (1998-02): Faserverstärkte Kunststoffe – Bestimmung der scheinbaren interlaminaren Scherfestigkeit nach dem Dreipunktverfahren mit kurzem Balken
 
|DIN EN ISO 14130 (1998-02): Faserverstärkte Kunststoffe – Bestimmung der scheinbaren interlaminaren Scherfestigkeit nach dem Dreipunktverfahren mit kurzem Balken
 
|}
 
|}
  
 
[[Kategorie:Biegeversuch]]
 
[[Kategorie:Biegeversuch]]

Aktuelle Version vom 1. Oktober 2024, 09:49 Uhr

Ein Service der
Logo psm.jpg
Polymer Service GmbH Merseburg
Tel.: +49 3461 30889-50
E-Mail: info@psm-merseburg.de
Web: https://www.psm-merseburg.de
Unser Weiterbildungsangebot:
https://www.psm-merseburg.de/weiterbildung
PSM bei Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg

Biegeversuch Schubspannung

Ursachen für das Auftreten von Schubspannungen

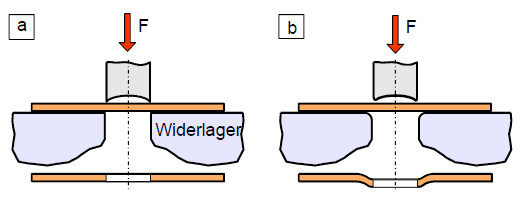
Bei der Biegeprüfung an Kunststoffen wird in Übereinstimmung mit den bevorzugten Normen der Biegeprüfung von Kunststoffen [1, 2] angenommen, dass im Prüfkörper eine reiner Normalspannungszustand vorliegt. In Analogie hierzu soll beim Scher- oder Stanzversuch ein reiner Scherspannungszustand vorliegen. Beim Vorliegen einer exakten Justierung und einem scharfen Stanzwerkzeug (Bild 1a) wird somit ein qualitätsgerechtes Ergebnis erzielt. Im Fall eines stumpfen Stanzmessers, Abrundungen an den Widerlagern oder einem zu großen Auflagerabstandes wird zusätzlich eine Durchbiegung erzeugt, die zu einem fehlerhaften Produkt führt (Bild 1b).

Biegeversuchschubspannung1.jpg

Bild 1: Einfluss von Biegung im Stanzprozess

Umgekehrt kann also ein zu geringer Auflagerabstand oder nicht angepasste Auflagerradien eine unzulässig hohe Schubspannung im Querschnitt erzeugen. Dieser Spannungsanteil wird zwar in der Berechnung nicht berücksichtigt, er führt aber im Regelfall zu einer Verringerung der Kennwerte des Biegeversuchs. Das Auftreten der Schubspannung im Biegeversuch kann mit Hilfe von Bild 2 veranschaulicht werden [3, 4].

Enstehung und Verteilung von Schubspannungen im Biegeprüfkörper

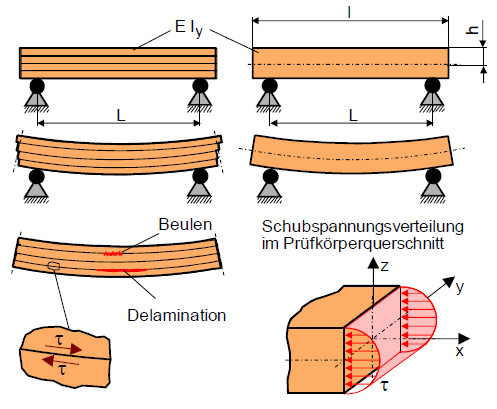
Bei Annahme eines Biegeträgers (Bild 2 rechts) oder vier einzelnen übereinander gelegten Biegebalken (Bild 2 links) mit identischer Geometrie und aus dem gleichen Werkstoff, also vergleichbarer Biegesteifigkeit EIy, wird sich bei Belastung eine annähernd gleiche Durchbiegung einstellen. Beim Vergleich der Randkontur wird sich bei dem Biegeträger ein ebener Querschnitt einstellen, während sich die Biegebalken einzeln verformen und damit eine treppenförmige Kontur des Querschnitts hervorrufen.

Erzeugt man eine Lamitatstruktur des Biegeträgers mit vier verklebten Einzelschichten, dann erkennt man, dass zur Aufrechterhaltung der ebenen Randkontur Kräfte zwischen den Schichten wirken, die sich in einer Schubspannung äußern. Wird die Belastung durch die Schubspannung zu groß, dann treten, wie bekannt, auf der oberen Druckseite Beuleffekte oder auf der unteren Zugseite Delaminationen zwischen den Einzelschichten auf.

Biegeversuchschubspannung2.jpg

Bild 2: Entstehung und Verteilung der Schubspannung im Biegeversuch

Die Schubspannung erreicht ihr Maximum im Bereich der neutralen Faser und weist eine parabolische Verteilungsfunktion auf (Bild 2). Zur Vermeidung unzulässiger Schubspannungseinflüsse im Biegeversuch muss nach DIN EN ISO 178 [1] ein Längen-Dicken-Verhältnis l/h = 20, bzw. ein Stützweiten-Dicken-Verhältnis von L/h = 16 eingehalten werden. Aufgrund der Schubempfindlichkeit von Laminaten beträgt in diesem Fall das Stützweiten-Dicken-Verhältnis L/h = 20 – 25. Aus dem sogenannten „Short-Beam Bend Test“, d. h. dem Biegeversuch mit engem Auflagerabstand kann man dann an Laminaten die Interlaminare Scherfestigkeit (ILSF) ermitteln [5, 6].


Siehe auch


Literaturhinweise

[1] DIN EN ISO 178 (2019-08): Kunststoffe – Bestimmung der Biegeeigenschaften
[2] DIN EN ISO 14125 (2011-05): Faserverstärkte Kunststoffe – Bestimmung der Biegeeigenschaften; Technical Corrigendum Cor.1:2001 + Amd.1:2011
[3] Bierögel, C.: Biegeversuch an Kunststoffen. In: Grellmann, W., Seidler, S. (Hrsg.): Kunststoffprüfung. Carl Hanser Verlag, München (2024) 4. Auflage, S. 141–151 (ISBN 978-3-446-44718-9; E-Book: ISBN 978-3-446-48105-3; siehe AMK-Büchersammlung unter A 23)
[4] Bierögel, C., Grellmann, W.: Bend loading. In: Grellmann, W., Prof. Sabine Seidler: Mechanical and Thermomechanical Properties of Polymers. Landolt-Börnstein, Volume VIII/6A3, Springer Verlag, Berlin (2014) 164–191, (ISBN 978-3-642-55165-9; siehe AMK-Büchersammlung unter A 16)
[5] Altstädt, V.: Prüfung von Verbundwerkstoffen. In: Grellmann, W., Seidler, S. (Hrsg.): Kunststoffprüfung. Carl Hanser Verlag, München (2024) 4. Auflage, S. 549–550 (ISBN 978-3-446-44718-9; E-Book: ISBN 978-3-446-48105-3; siehe AMK-Büchersammlung unter A 23)
[6] DIN EN ISO 14130 (1998-02): Faserverstärkte Kunststoffe – Bestimmung der scheinbaren interlaminaren Scherfestigkeit nach dem Dreipunktverfahren mit kurzem Balken
Abgerufen von „https://wiki.polymerservice-merseburg.de/index.php?title=Biegeversuch_Schubspannung&oldid=9332“