Zum Inhalt springen

Craze-Typen

Aus Lexikon der Kunststoffprüfung
Ein Service der
Polymer Service GmbH Merseburg
Tel.: +49 3461 30889-50
E-Mail: info@psm-merseburg.de
Web: https://www.psm-merseburg.de
Unser Weiterbildungsangebot:
https://www.psm-merseburg.de/weiterbildung
PSM bei Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg

Craze-Typen (Autor: Prof. Dr. G. H. Michler)

Einführung

Ein Craze (engl.: Haarriss) enthält im Gegensatz zu einem Riss hochorientiertes plastisch verstrecktes Material. Der mikromechanische Bildungsmechanismus wird als Crazing oder Craze-Mechanismus bezeichnet und steht im engen Zusammenhang mit dem Versagen durch Bruch. Die Bildung von Crazes hat aber auch positive Effekte bzgl. des Werkstoffverhaltens indem sich die Crazes infolge der Verstreckung des polymeren Materials am Lasttragen beteiligen und somit die Zähigkeit steigern. Die Aufklärung der Bildungsmechanismen der Crazes erfordert eine stärkere werkstoffwissenschaftliche Durchdringung, wobei die Aufklärung der Strukturen bis zur atomaren Ebene mit den Methoden der Elektronenmikroskopie eine entscheidende Rolle spielt. Für das wichtige Gebiet der mechanischen Eigenschaften erfordert dies die Nutzung der Methoden der Mikro- oder Nanomechanik. Mit deren Hilfe können nanostrukturierte Polymere mit verbesserten Eigenschaften gewonnen werden. Auf einige Möglichkeiten der Verbesserung von Kunststoffen wird in diesem Artikel eingegangen [1–3].

Crazes, crazeartige Prozesse und Scherbänder

  • Crazes sind lokale plastische Prozesse, die in lokalisierten, bandartigen Zonen konzentriert sind und dem Riss bzw. Bruch vorausgehen. Sie stellen ein generelles Phänomen dar und treten außer in Polymeren auch in verschiedenen anderen Materialien auf.
  • Anorganische Gläser sind typische Beispiele für amorphe, spröde Materialien, in denen sich Brüche sehr schnell, oft schlagartig ausbreiten (siehe auch Rissausbreitung). Vor der Risspitze enthüllen sie aber in elektronenmikroskopischen Untersuchungen kleine plastische Zonen [4].
  • Amorphe Metalle (oder metallische Gläser) bilden sich bei einigen Metalllegierungen bei extrem schneller Abkühlung aus der Schmelze. Sie zeigen bei Dehnbelastung lokale plastische Zonen von bis über 50 μm Länge und bis zu 1 μm Dicke [5].
  • In Metallen ist die Rissbildung und -ausbreitung mitunter mit der Bildung von Mikrolöchern und plastisch verstreckten Fibrillen zwischen den Löchern verbunden, was an grobe Crazestrukturen erinnert.
  • Knochen ist von der Morphologie her ein Nanokomposit mit einem sprödartigen Bruchverhalten. Besonders im Rissspitzenbereich werden die Rissufer durch Fibrillen aus Kollagen mit Hydroxylapatikriställchen überspannt und erscheinen wie crazeartige Strukturen.
  • Trocknender Schlamm, Stärkebrei oder abkühlende Lava baut Schrumpfspannungen auf, die zu einem makroskopischen Rissmuster führen. Mit fortgesetzter Trocknung bauen sich Schrumpfspannungen auf, die zuerst dickere Risse mit größeren Abständen und dann schrittweise dünnere und kleinere Risse erzeugen [6]. Die Risse in Lava ordnen sich mitunter während des Verfestigungsprozesses in regelmäßigen, hexagonalen Mustern an und treten dann in Säulenform auf.

Crazes wurden zuerst ausführlich in den amorphen Polymeren untersucht. Die makroskopische Erscheinung ähnlich zu Rissen führten zu dem Namen Craze. Die angelsächsische Bezeichnung „craze“ geht auf verschiedene mittelenglische Formen zurück, die alle die Bedeutung von “brechen“ haben. Auf diese alte Bedeutung weisen noch die Haarrisse (Krakelee) in der Glasur von Töpferwaren oder Porzellan hin (das heutige Wort „crazy“ weist wohl auch auf den Ursprung „verrrückt“ im Kopf hin). Mit dieser Bedeutung beschreibt der Begriff „Craze“ nur die phänomenologische Seite, ist aber von der Sache her nicht zutreffend [3]. Bei den Crazes handelt es sich nicht um Risse, sondern um scharf lokalisierte, in Mikrobereichen vorliegende Deformationszonen. Durch die Struktur der Crazes sind sie am Lasttragen beteiligt und verzögern so eine schnelle, sprödartige Rissausbreitung.

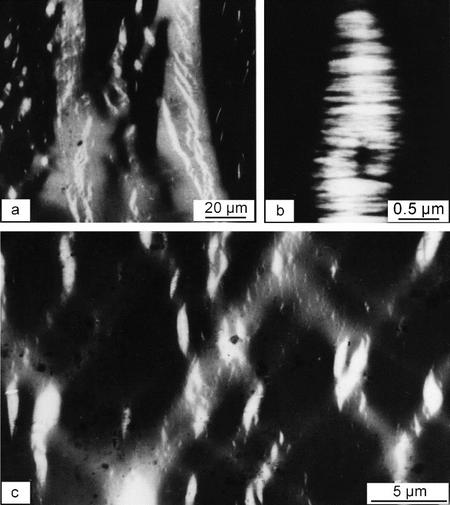
Die genaue Kenntnis der Struktur von Crazes beruht hautpsächlich auf elektronenmikroskopischen Untersuchungen und auch auf Röntgenstreumessungen. Am bekanntesten sind Crazes von den amorphen, sprödartigen Polymern her, wie Polystyrol (Kurzzeichen: PS), Polymethylmethacrylat (Kurzzeichen: PMMA) und vielen anderen. Einen Überblick über Craze-Muster in Dehnstäben von PS und PMMA zeigt Bild 1 und die typische fibrillare Innenstruktur ist in Bild 2 erkennbar.

Bild 1: Zugprüfkörper mit Crazes nach einer Belastung bis kurz vor den Bruch in Gesamtansicht (links) und in geringen lichtoptischen Vergrösserungen aus den Stabmitten (rechts)
a) Polystyrol (PS)
b) Polymethylmethacrylat (PMMA)

Die Rissausbreitung in den Crazes erfolgt durch sukzessives Überspannen und Reißen der Crazefibrillen (Bild 2). Es erfolgt eine ständige Reproduktion der Spannungskonzentration an der Rissspitze im Craze, und da die Crazes oft sehr lang sind, erfolgt eine schnelle, sprödartige Rissausbreitung ohne eine Tendenz zur Rissspitzenverrundung.

Bild 2: Rissausbreitung in einem Craze in Polystyrol mit sukzessivem Strecken, Überspannen und Reißen der Craze-Fibrillen
a) Überblick
b) höhere Vergrößerung
(in-situ-Deformation im Höchstspannungs-Transmissionselektronenmikroskop (HEM), Dehnungsrichtung senkrecht

Außer den Crazes mit Fibrillen (Craze-Typ I) treten in manchen Polymeren auch Crazes ohne eine Fibrillierung, d. h. mit homogener Innenstruktur auf (Craze-Typ II). Die beiden Typen I und II von Crazes finden sich auch gemeinsam mit Scherbändern – eine Koexistenz aller drei Typen von Deformationszonen demonstriert Bild 3 in einem Polyvinylchlorid-Material (Kurzzeichen: PVC). Das Auftreten dieser Deformationszonen ist auch mit dem Verschlaufungsnetzwerk und der Verschlaufungsdichte verbunden. Mit zunehmender Verschlaufungsdichte (abnehmendes Verschlaufungs-Molekulargewicht und abnehmender Abstand) erfolgt die Koexistenz von fibrillierten und homogenen Crazes mit einem Übergang zu homogenen Crazes und Scherbändern [7, 8].

Bild 3: Koexistenz von isolierten, fibrillierten Crazes I (Bild 3b), von fibrillierten Crazes II in einer homogenen Deformationszone (Bild 3a), und Scherbändern zwischen Rissspitze und Crazes (Bild 3c) in einem PVC, deformierter Dünnschnitt im HEM, Dehnungsrichtung horizontal

Einfluss von Partikeln auf Deformationsmechanismen

a) Initiierte Deformationsmechanismen

Partikel können auf vielfältige Art einen Bruchverlauf und damit die mechanischen Eigenschaften beeinflussen [9]. Größere Partikel oder größere Defekte können vor dem sich ausbreitenden Hauptriss aus der Umgebung gelöst werden und so einen Sekundärriss erzeugen. Bei der Überlagerung des Seundärrisses mit dem sich ausbreitenden Riss entstehen parabelförmige Muster mit dem Defekt als (mathematischer) Brennpunkt der Parabel.

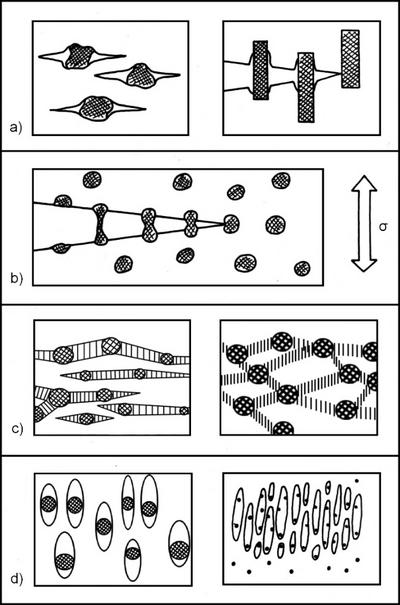
Defekte oder Partikel in einer Matrix können aber statt einem Sprödbruch auch duktile Mechanismen initieren. Bild 4 illustriert verschiedene Fälle von Deformationsmechanismen, die durch unterschiedliche partikelartige Strukturen initiiert werden können:

a) Vielfach-Lochinitierung und Mikrorissbildung: Loslösung von Teilchen oder Fasern erzeugen neue Oberflächen und Mikrorisse. Große Defekte initiieren Sekundärrise.
b) Brückenbildungsmechanismus: Liegen duktile, weichere Teilchen vor, die gut an die Matrix angebunden sind (gute Grenzflächenhaftung), können sie die Ufer von gebildeten Rissen überspannen und eine Rissausbreitung verzögern. Ein weiterer Vorteil ist der Effekt, dass Rissspitzen an den weichen Teilchen gestoppt werden können (Rissstoppmechanismus – Bild 5).
c) Vielfachinitiierung plastischer Verformungen: Duktile, weiche Teilchen wie in b) wirken in einer härteren Matrix als Spannungskonzentratoren und initiieren in den Äquatorialzonen oder zwischen den Teilchen lokale Fließprozesse (Scherdeformationen oder in glasartigen Polymeren Fließzonen, die Crazes).
d) Nanolochbildung mit Fibrillierungen: Liegen Partikel im Größenbereich von Subμm vor, kann bei geringer Grenzflächenhaftung zwischen Partikeln und Matrix nach Loslösung, Mikrolochbildung und Spannungskonzentration in den angrenzenden Matrixbereichen bei einem duktilen Material lokales Fließen bis zu einer Fibrillierung initiiert werden. Voraussetzung hierbei ist, dass die Subμm-Teilchen nur eine enge Teilchengrößenerteilung aufweisen (d. h. etwa gleich klein sind) und homogen verteilt sind. Große Partikel und räumlich inhomogen verteilte Partikel führen mehr zu Fall a).

Bild 4: Verschiedene lokale Mechanismen, initiiert durch Teilchen oder partikuläre Strukturen

a) Lochbildung und Vielfach-Rissbildung
b) Brückenmechanismus
c) Vielfachinitiierung von lokalen Deformationszonen oder Scherbändern
d) Lochbildung an Mikroteilchen (im Unterschied zu größeren Partikeln im Fall a) mit Fließprozessen zwischen den Teilchen bis hin zur Fibrillierung

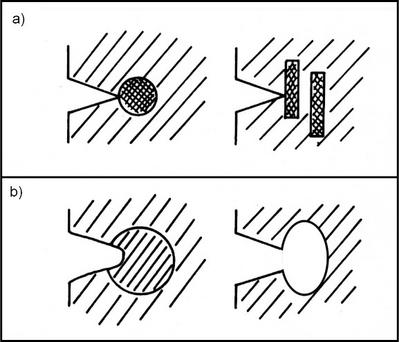
Teilchen in einer Matrix können aber auch die Ausbreitung von Rissen behindern oder stoppen – Bild 5. Rissstopp oder Reduzierung der Rissausbreitungsgeschwindigkeit ist erreichbar durch:

a) Auftreffen eines Risses in ein Gebiet höherer Festigkeit, etwa an harte Teilchen oder steife Fasern
b) Eindringen eines Risses in ein Teilchen höherer Duktilität oder auch in einen Hohlraum (Mikroloch). Durch Verrundung der Rissspitze (crack tip blunting) wird die Spannungskonzentration (siehe Bruchmechanik) an der Rissspitze deutlich reduziert

Bild 5: Rissstopp-Mechanismen – Belastungsrichtung senkrecht
a) Rissstopp an steiferen, härtern Partikeln oder Fasern
b) Rissstopp an weicheren Teilchen oder Mikrohohlräumen durch Rissabstumpfung

b) Spannungskonzentrationen an Teilchen

Wie bei Bild 4 erwähnt, spielen Teilchen oder allg. partikuläre Inhomogenitäten im Deformationsverhalten aller Materialien eine Rolle, da sie lokale Spannungskonzentrationen hervorrufen. Eine von außen wirkende Belastung erzeugt in einem elastischen Körper in der Umgebung eines Teilchens vor allem in den Zonen senkrecht zur Belastungsrichtung (äquariale Zonen) Spannungskonzentrationen. Dabei ist die Spannungskomponente σδδ, die parallel zur Teilchen/Matrix-Grenzfläche in der umgebenden Matrix wirkt, von besonderer Bedeutung. Die Spannungskomponente σδδ für ein weiches Teilchen in einer elastischen Umgebung erreicht direkt am Äquator (δ = 90°) fast das doppelte der angelegten Spannung (Spannungsanalysen nach Goodier [10]). In Richtung zu den Polen (δ = 0°) nimmt die Spannung ab und wechselt von einer Zugspannung in eine Kompressionsspannung (σδδ < 0). Von Einfluss ist auch der Unterschied im Teilchenmodul GP relativ zum Matrixmodul GM (GP/GM). Die maximale Spannungskonzentration σδδ tritt auf, wenn weiche Teilchen (kleiner Teilchenmodul GP) in einer härteren Matrix vorliegen.

Sind in der Matrix viele weichere Teilchen in engem Abstand A vorhanden, überlagern sich die Spannungsfelder der einzelnen Partikel. Die Spannungskonzentrationen sind wesentlich für die Einleitung von Deformationszonen und damit der Steigerung der Zähigkeit.

Siehe auch


Literaturhinweise

[1] Michler, G. H.: Werkstoffwissenschaft und Kunststoffe. Schriften der Sudetendeutschen Akademie der Wissenschaften und Künste. Band 43, Forschungsbeiträge der Naturwissenschaftlichen Klasse, München (2024) 27–58; siehe AMK-Büchersammlung unter F 33
[2] Michler, G. H.: Mechanik–Mikromechanik–Nanomechanik. Vom Eigenschaftsverstehen zur Eigenschaftsverbesserung. SpringerSpektrum (2024), ISBN 978-3-662-66965-5; e-book: ISBN 978-3-66966-2; https://doi.org/10.1007/978-3-662-66966-2; siehe AMK-Büchersammlung unter F 34
[3] Michler, G. H.: Michler, G. H.: Kunststoff-Mikromechanik: Morphologie, Deformations- und Bruchmechanismen; Carl Hanser München (1992); ISBN 3-446-17068-5, siehe AMK-Büchersammlung unter F 4
[4] Hopfe, J., Albrecht, R., Hillebrandt, R., Pippel, A., Schmidt, V.: HREM investigation of highly strained inorganic glasses of different compositions. Ultramicroscopy 15, 71–80 (1984); https://doi.org/10.1016/0304-3991(84)90076-7
[5] Takayama, S., Maddin, R.: Fracture of amorphous Ni-Pd-P alloys. Philos. Mag. 32 (1975) 457–470; https://doi.org/10.1080/14786437508219968
[6] Müller, G.: Physikalische Blätter Nr.10, 55, 35–37 (1999)
[7] Berger, L. L.; Kramer, E. J.: Microdeformation in partially compatible blends of poly(styrene-acrylonitrile) and polycarbonate. J. Mater. Sci. 22, 2739–2750 (1987); https://doi.org/10.1007/BF01086466
[8] Kramer, E. J.: Craze fibril formation and breakdown. Polym. Eng. Sci. 24, 761–769 (1984) https://doi.org/10.1002/pen.760241006
[9] Grellmann, W., Seidler, S. (Hrsg.): Deformation und Bruchverhalten von Kunststoffen. Springer Verlag, Berlin Heidelberg (1998); ISBN 978-3-642-63718-6
[10] Goodier, I. N.: Concentration of stress around spherical and cylindrical inclusions and flaws. J. Appl. Mech. Trans. ASME 55 (1933) 39–44

Weblinks

Abgerufen von „https://wiki.polymerservice-merseburg.de/index.php?title=Craze-Typen&oldid=9901“