Deformation: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
|||
| (12 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
< | {{PSM_Infobox}} | ||
<span style="font-size:1.2em;font-weight:bold;">Deformation</span> | |||
== Anisotrope Deformation == | == Anisotrope Deformation == | ||
In einer Vielzahl von | In einer Vielzahl von [[Kunststoffe]]n ist der Zusammenhang zwischen Spannung und Dehnung schon bei kleinen Deformationen nichtlinear ('''Bild 1a'''). Wie das '''Bild 1''' aber zeigt, besteht trotzdem Proportionalität zwischen der Spannung und der Dehnung. In diesem Fall ist im Gegensatz zu den meisten metallischen Werkstoffen jedoch die Voraussetzung der linearen Proportionalität nicht erfüllt. | ||
Ein anderes nichtlineares Verhalten zeigt ein bis zu hohen Dehnungen be- und entlasteter Gummi oder elastomerer Werkstoff (Bild | Ein anderes nichtlineares Verhalten zeigt ein bis zu hohen Dehnungen be- und entlasteter Gummi oder [[Elastomere|elastomerer Werkstoff]] ('''Bild 1b'''). Liegt die Entlastungskurve unter der Belastungskurve, wird im Dehnungszyklus Energie dissipiert. Dieses Phänomen ist als Hysterese bekannt. Die Bezeichnung ist jedoch nur dann anwendbar, wenn der Werkstoff in die Nulldeformation zurückkehrt. Ist der elastomere Werkstoff gefüllt oder verstärkt, dann tritt wie auch bei anderen Kunststoffen, eine permanente Verschiebung auf, auch wenn diese unter der Dehnung bei der [[Streckspannung]], d. h. im elastischen bzw. [[Viskoelastisches Werkstoffverhalten|viskoelastischen Bereich]] liegt. | ||
Duktile Kunststoffe weisen oft eine gut definierte Streckspannung mit Dehnungen an der Streckspannung von 5–10% auf (Bild | Duktile [[Kunststoffe]] weisen oft eine gut definierte [[Streckspannung]] mit Dehnungen an der Streckspannung von 5–10 % auf ('''Bild 1c'''). Nachfolgend wird dann in der Regel eine plastische Deformation registriert, deren absoluter Betrag wesentlich von der [[Deformationsgeschwindigkeit]] abhängt. In Abhängigkeit von der Art des [[Kunststoffe]]s kann dann auch eine Verfestigung auftreten. | ||
[[Datei:anisotrope_deformation.jpg]] | [[Datei:anisotrope_deformation.jpg]] | ||
{| | |||
Bild: Schematische Darstellung anisotroper Deformationen | |- valign="top" | ||
a) nichtlinear elastische Deformation | |width="50px"|'''Bild 1:''' | ||
b) mechanische Hysterese | |width="600px" |Schematische Darstellung anisotroper Deformationen | ||
c) Streckspannung und plastische Deformation | a) nichtlinear elastische Deformation<br> | ||
b) mechanische Hysterese<br> | |||
c) Streckspannung und plastische Deformation<br> | |||
|} | |||
== Viskose Deformation == | == Viskose Deformation == | ||
| Zeile 26: | Zeile 28: | ||
<li>Die zur Verformung aufgewendete Arbeit wird vom Werkstoff vollständig dissipiert.</li></ol> | <li>Die zur Verformung aufgewendete Arbeit wird vom Werkstoff vollständig dissipiert.</li></ol> | ||
Strukturell findet bei viskosem Verhalten eine Relativverschiebung benachbarter Struktureinheiten (Moleküle bzw. Molekülsequenzen bei | Strukturell findet bei viskosem Verhalten eine Relativverschiebung benachbarter Struktureinheiten (Moleküle bzw. Molekülsequenzen bei [[Polymer]]werkstoffen) statt. Die dabei zu überwindenden Reibungskräfte sind abhängig von der [[Verformungsgeschwindigkeit]]. Wird ein linearer Zusammenhang zwischen Spannung und [[Deformationsgeschwindigkeit]] beobachtet, so liegt NEWTON‘sches Werkstoffverhalten vor. Dieses wird durch die Viskosität <math>\eta</math> als [[Werkstoffkenngröße]] charakterisiert. | ||
'''Literaturhinweis''' | |||
* [[Grellmann,_Wolfgang|Grellmann, W.]], [[Seidler,_Sabine|Seidler, S.]] (Hrsg.): Kunststoffprüfung. Carl Hanser Verlag, München (2024) 4. Auflage, S. 82–84 (ISBN 978-3-446-44718-9; E-Book: ISBN 978-3-446-48105-3; siehe [[AMK-Büchersammlung]] unter A 23) | |||
== Elastische Deformation == | == Elastische Deformation == | ||
Eine elastische Deformation ist dadurch gekennzeichnet, dass die von äußeren Kräften geleistete Arbeit reversibel als Formänderungsenergie gespeichert wird. Besteht zwischen Kraft und Verformung eine lineare unverzögerte Wechselwirkung, dann liegt ein linear-elastisches Werkstoffverhalten vor. Hier gilt das HOOKE’sche Gesetz (siehe [[Energieelastizität]]), wobei der [[Elastizitätsmodul]] die Federkonstante des Werkstoffs beschreibt. | |||
Anders ausgedrückt wird das mechanische Verhalten immer dann als elastisch bezeichnet, wenn ein umkehrbar eindeutiger Zusammenhang zwischen dem Spannungs- und Deformationszustand besteht. Es ist damit im mechanischen wie im thermomechanischen Sinne völlig reversibel. | |||
Entsprechend der unterschiedlichen thermodynamischen Ursachen unterscheidet man zwischen Energie- und Entropieelastizität. | |||
'''Literaturhinweis''' | |||
[[Grellmann,_Wolfgang|Grellmann, W.]], [[Seidler,_Sabine|Seidler, S.]] (Hrsg.): Kunststoffprüfung. Carl Hanser Verlag, München (2024) 4. Auflage, S. 80 (ISBN 978-3-446-44718-9; E-Book: ISBN 978-3-446-48105-3; siehe [[AMK-Büchersammlung]] unter A 23) | |||
== Plastische Deformation == | == Plastische Deformation == | ||
Die plastische Deformation ist eine Kombination von reversiblen und irreversiblen Prozessen. Im Unterschied zum viskosen ([[Viskoelastisches Werkstoffverhalten|viskoelastischen]]) Verhalten treten diese jedoch nicht gleichzeitig nebeneinander auf, sondern sie sind durch eine Fließgrenze σ<sub>F</sub> voneinander getrennt. Unterhalb dieser Fließgrenze ist das Werkstoffverhalten elastisch oder viskoelastisch, oberhalb finden irreversible Fließprozesse statt (siehe '''Bild 2a''') [1]. | |||
Plastisches Deformationsverhalten wird bei vielen amorphen und teilkristallinen [[Kunststoffe]]n beobachtet. Unter uniaxialer Zugbeanspruchung kommt es, wie in '''Bild 2b''' dargestellt, in Form einer [[Streckspannung]] σ<sub>s</sub> zum Ausdruck. Hierbei handelt es sich um ein lokales Maximum in der [[Zugversuch#Zugversuch, Spannungs-Dehungs-Diagramm|Spannungs-Dehnungs-Kurve]], welches üblicherweise bei Dehnungen zwischen etwa 5 und 25 % beobachtet wird. | |||
[[Datei:plastische_deformation.jpg]] | |||
{| | |||
|- valign="top" | |||
|width="50px"|'''Bild 2:''' | |||
|width="600px" |Zusammenhang zwischen Spannung und Dehnung bei plastischem Materialverhalten: Modell (a) und Kunststoff (b) (1: scheinbarer Kurvenverlauf; 2: wahrer Kurvenverlauf)<br> | |||
|} | |||
Das Auftreten der Streckspannung steht mit einer lokalen Querschnittsverringerung am [[Prüfkörper]] in Zusammenhang, die auch als Einschnürung bezeichnet wird. In der Einschnürzone finden irreversible Verformungen von mehreren hundert Prozent statt. Infolge dieser Inhomogenität ergeben sich große Unterschiede zwischen der nominellen und tatsächlichen Spannung bzw. Dehnung. Mit der Ermittlung [[Zugversuch Wahres Spannungs-Dehnungs-Diagramm|wahrer Spannungs-Dehnungs-Diagramme]] konnte gezeigt werden, dass es sich bei dem Spannungsabfall nach Überschreiten der Streckspannung häufig nur um einen scheinbaren Geometrieeffekt handelt [2]. | |||
Die Höhe der für das Einsetzen plastischer Fließprozesse erforderlichen Fließspannung ist abhängig vom Spannungszustand sowie von der Temperatur und der [[Prüfgeschwindigkeit|Beansprunchungsgeschwindigkeit]]. Der Einfluss des Spannungszustandes kann im Allgemeinen durch die aus der klassischen Mechanik bekannten Fließspannungshypothesen beschrieben werden [3]. Hinsichtlich der bei der plastischen Deformation ablaufenden [[Deformationsmechanismen]] weisen amorphe und teilkristalline [[Kunststoffe]] jedoch signifikante Unterschiede auf. Bei amorphen Kunststoffen findet die plastische Deformation im Glaszustand statt. Hier bewirken lokale molekulare Bewegungsprozesse unter der Einwirkung der Spannung die Bildung plastizierter Mikrodomänen, deren Wachstum und Vereinigung makroskopisch zur plastischen Deformation in Form von [[Scherbandbildung|Scherbändern]] oder [[Crazing|Crazes]] führen [4, 5]. Bei teilkristallinen Kunststoffen findet die plastische Deformation i. Allg. oberhalb der [[Glastemperatur]] in den amorphen Bereichen statt. Hier stellen kristallographische Gleitprozesse den entscheidenden Deformationsschritt dar [6‒8] in dessen Ergebnis die lamellare Ausgangsstruktur in eine Fibrillenstruktur überführt wird [9, 10]. Aus der Betrachtung der [[Deformationsmechanismen]] wird deutlich, dass die mikroskopischen Prozesse, die zur plastischen Deformation führen, bereits weit unterhalb der Fließgrenze einsetzen. Häufig lassen sie sich schon bei einer [[Beanspruchung]] im [[Linear-viskoelastisches Verhalten|linear-viskoelastischen Bereich]] nachweisen, so dass Zusammenhänge zwischen Relaxationszeitspektrum und plastischem Verhalten hergestellt werden können [11]. | |||
Im Ergebnis der plastischen Deformation findet eine Orientierung der Makromoleküle statt. Die damit verbundenen Eigenschaftsänderungen sind Ziel zahlreicher Verarbeitungsprozesse. Durch die molekulare Orientierung werden entropieelastische Rückstellkräfte (siehe [[Entropieelastizität]]) hervorgerufen, die der plastischen Deformation entgegenwirken und Ursache für die bei großen Verformungen zu beobachtenden Verfestigungsprozesse sind. Bei weiterer Steigerung der [[Beanspruchung]] kommt es zum lokalen Bruch überlasteter Polymerketten, der dem makroskopischen Versagen oder [[Bruch]] des Materials vorausgeht. | |||
==Siehe auch== | |||
* [[Deformationsmechanismen]] | |||
* [[Energieelastizität]] | |||
* [[Entropieelastizität]] | |||
* [[Crazing]] | |||
* [[Brucharten]] | |||
* [[Zugversuch Ereignisbezogene Interpretation]] | |||
* [[Scherbandbildung]] | |||
'''Literaturhinweise''' | |||
{| | |||
|-valign="top" | |||
|[1] | |||
|[[Grellmann,_Wolfgang|Grellmann, W.]], [[Seidler,_Sabine|Seidler, S.]] (Hrsg.): Kunststoffprüfung. Carl Hanser Verlag, München (2024) 4. Auflage, S. 90–92 (ISBN 978-3-446-44718-9; E-Book: ISBN 978-3-446-48105-3; siehe [[AMK-Büchersammlung]] unter A 23) | |||
|-valign="top" | |||
|[2] | |||
|G’Sell, C., Jonas, J. J.: Determination of the Plastic Behaviour of Solid Polymers at Constant True Strain Rate. J. Mater. Sci. 14 (1979) 583‒591 | |||
|-valign="top" | |||
|[3] | |||
|Ward, I. M.: Review: The Yield Behavior of Polymers. J. Mater. Sci. 6 (1971) 1397‒1417 | |||
|-valign="top" | |||
|[4] | |||
|Argon, A. S.: A Theory for the Low-temperature Plastic Deformation of Glassy Polymers. Philos. Mag. 28 (1973) 839‒865 | |||
|-valign="top" | |||
|[5] | |||
|Perez, J.: Physics and Mechanics of Amorphous Polymers. A. A. Balkema Verlag, Rotterdam (1998) (e-Book ISBN 978-0-2037-4333-1) | |||
|-valign="top" | |||
|[6] | |||
|Bowden, P. B., Young, R. J.: Deformation Mechanisms in Crystalline Polymers. J. Mater. Sci. 9 (1974) 2034‒2051 | |||
|-valign="top" | |||
|[7] | |||
|Lin, L., Argon, A. S.: Structure and Plastic Deformation of Polyethylene. J. Mater. Sci. 29 (1994) 294‒323 | |||
|-valign="top" | |||
|[8] | |||
|Christ, B.: Plastic Deformation of Polymers. In: Thomas, E. I. (Ed.): Materials Science and Technology, Vol. 12: Structure and Properties of Polymers. Wiley VCH Verlag, Weinheim (2002) (ISBN 978-3-52726825-2) | |||
|-valign="top" | |||
|[9] | |||
|Peterlin, A.: Plastic Deformation of Polyethylene by Rolling and Drawing. Kolloid Z. u. Z.: Polymer 233 (1969) 857‒862 | |||
|-valign="top" | |||
|[10] | |||
|Petermann, J., Kluge, W., Gleiter, H.: Electron Microscopic Investigation of the Molecular Mechanism of Plastic Deformation of Polyethylene and Isotactic Polystyrene Crystals. Polym. Sci. B-Polym. Phys. 17 (1979) 1043‒1051 | |||
|-valign="top" | |||
|[11] | |||
|Bauwens-Crowett, C., Bauwens, C. J., Homes, G.: Tensile Yield Stress Behavior of Glassy Polymers. J. Polym. Sci. A-2-Polym. Chem. 7 (1969) 735‒742 | |||
|} | |||
[[Kategorie:Deformation]] | |||
Aktuelle Version vom 7. Oktober 2024, 11:20 Uhr
| Ein Service der |
|---|

|
| Polymer Service GmbH Merseburg |
| Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de |
| Unser Weiterbildungsangebot: https://www.psm-merseburg.de/weiterbildung |
| PSM bei Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg |
Deformation
Anisotrope Deformation
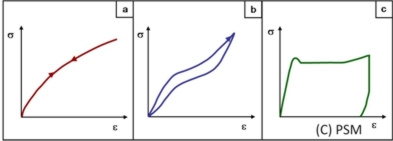
In einer Vielzahl von Kunststoffen ist der Zusammenhang zwischen Spannung und Dehnung schon bei kleinen Deformationen nichtlinear (Bild 1a). Wie das Bild 1 aber zeigt, besteht trotzdem Proportionalität zwischen der Spannung und der Dehnung. In diesem Fall ist im Gegensatz zu den meisten metallischen Werkstoffen jedoch die Voraussetzung der linearen Proportionalität nicht erfüllt.
Ein anderes nichtlineares Verhalten zeigt ein bis zu hohen Dehnungen be- und entlasteter Gummi oder elastomerer Werkstoff (Bild 1b). Liegt die Entlastungskurve unter der Belastungskurve, wird im Dehnungszyklus Energie dissipiert. Dieses Phänomen ist als Hysterese bekannt. Die Bezeichnung ist jedoch nur dann anwendbar, wenn der Werkstoff in die Nulldeformation zurückkehrt. Ist der elastomere Werkstoff gefüllt oder verstärkt, dann tritt wie auch bei anderen Kunststoffen, eine permanente Verschiebung auf, auch wenn diese unter der Dehnung bei der Streckspannung, d. h. im elastischen bzw. viskoelastischen Bereich liegt.
Duktile Kunststoffe weisen oft eine gut definierte Streckspannung mit Dehnungen an der Streckspannung von 5–10 % auf (Bild 1c). Nachfolgend wird dann in der Regel eine plastische Deformation registriert, deren absoluter Betrag wesentlich von der Deformationsgeschwindigkeit abhängt. In Abhängigkeit von der Art des Kunststoffes kann dann auch eine Verfestigung auftreten.
| Bild 1: | Schematische Darstellung anisotroper Deformationen
a) nichtlinear elastische Deformation |
Viskose Deformation
Im Unterschied zum elastischen Verhalten zeichnet sich viskoses Verhalten durch eine vollständige Irreversibilität der Deformationsprozesse aus. Daraus folgt:
- Eine einmal aufgebrachte Verformung bleibt auch nach Entlastung erhalten, der Zusammenhang zwischen Spannung und Deformation ist nur unter Berücksichtigung der Vorgeschichte eindeutig, nicht jedoch umkehrbar eindeutig bestimmbar.
- Die zur Verformung aufgewendete Arbeit wird vom Werkstoff vollständig dissipiert.
Strukturell findet bei viskosem Verhalten eine Relativverschiebung benachbarter Struktureinheiten (Moleküle bzw. Molekülsequenzen bei Polymerwerkstoffen) statt. Die dabei zu überwindenden Reibungskräfte sind abhängig von der Verformungsgeschwindigkeit. Wird ein linearer Zusammenhang zwischen Spannung und Deformationsgeschwindigkeit beobachtet, so liegt NEWTON‘sches Werkstoffverhalten vor. Dieses wird durch die Viskosität als Werkstoffkenngröße charakterisiert.
Literaturhinweis
- Grellmann, W., Seidler, S. (Hrsg.): Kunststoffprüfung. Carl Hanser Verlag, München (2024) 4. Auflage, S. 82–84 (ISBN 978-3-446-44718-9; E-Book: ISBN 978-3-446-48105-3; siehe AMK-Büchersammlung unter A 23)
Elastische Deformation
Eine elastische Deformation ist dadurch gekennzeichnet, dass die von äußeren Kräften geleistete Arbeit reversibel als Formänderungsenergie gespeichert wird. Besteht zwischen Kraft und Verformung eine lineare unverzögerte Wechselwirkung, dann liegt ein linear-elastisches Werkstoffverhalten vor. Hier gilt das HOOKE’sche Gesetz (siehe Energieelastizität), wobei der Elastizitätsmodul die Federkonstante des Werkstoffs beschreibt.
Anders ausgedrückt wird das mechanische Verhalten immer dann als elastisch bezeichnet, wenn ein umkehrbar eindeutiger Zusammenhang zwischen dem Spannungs- und Deformationszustand besteht. Es ist damit im mechanischen wie im thermomechanischen Sinne völlig reversibel.
Entsprechend der unterschiedlichen thermodynamischen Ursachen unterscheidet man zwischen Energie- und Entropieelastizität.
Literaturhinweis
Grellmann, W., Seidler, S. (Hrsg.): Kunststoffprüfung. Carl Hanser Verlag, München (2024) 4. Auflage, S. 80 (ISBN 978-3-446-44718-9; E-Book: ISBN 978-3-446-48105-3; siehe AMK-Büchersammlung unter A 23)
Plastische Deformation
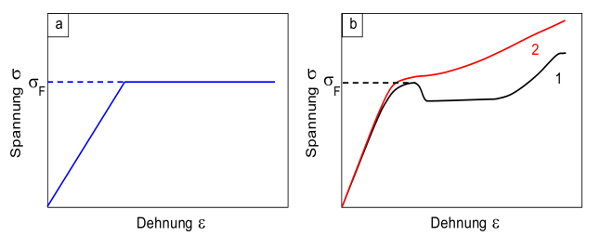
Die plastische Deformation ist eine Kombination von reversiblen und irreversiblen Prozessen. Im Unterschied zum viskosen (viskoelastischen) Verhalten treten diese jedoch nicht gleichzeitig nebeneinander auf, sondern sie sind durch eine Fließgrenze σF voneinander getrennt. Unterhalb dieser Fließgrenze ist das Werkstoffverhalten elastisch oder viskoelastisch, oberhalb finden irreversible Fließprozesse statt (siehe Bild 2a) [1].
Plastisches Deformationsverhalten wird bei vielen amorphen und teilkristallinen Kunststoffen beobachtet. Unter uniaxialer Zugbeanspruchung kommt es, wie in Bild 2b dargestellt, in Form einer Streckspannung σs zum Ausdruck. Hierbei handelt es sich um ein lokales Maximum in der Spannungs-Dehnungs-Kurve, welches üblicherweise bei Dehnungen zwischen etwa 5 und 25 % beobachtet wird.
| Bild 2: | Zusammenhang zwischen Spannung und Dehnung bei plastischem Materialverhalten: Modell (a) und Kunststoff (b) (1: scheinbarer Kurvenverlauf; 2: wahrer Kurvenverlauf) |
Das Auftreten der Streckspannung steht mit einer lokalen Querschnittsverringerung am Prüfkörper in Zusammenhang, die auch als Einschnürung bezeichnet wird. In der Einschnürzone finden irreversible Verformungen von mehreren hundert Prozent statt. Infolge dieser Inhomogenität ergeben sich große Unterschiede zwischen der nominellen und tatsächlichen Spannung bzw. Dehnung. Mit der Ermittlung wahrer Spannungs-Dehnungs-Diagramme konnte gezeigt werden, dass es sich bei dem Spannungsabfall nach Überschreiten der Streckspannung häufig nur um einen scheinbaren Geometrieeffekt handelt [2].
Die Höhe der für das Einsetzen plastischer Fließprozesse erforderlichen Fließspannung ist abhängig vom Spannungszustand sowie von der Temperatur und der Beansprunchungsgeschwindigkeit. Der Einfluss des Spannungszustandes kann im Allgemeinen durch die aus der klassischen Mechanik bekannten Fließspannungshypothesen beschrieben werden [3]. Hinsichtlich der bei der plastischen Deformation ablaufenden Deformationsmechanismen weisen amorphe und teilkristalline Kunststoffe jedoch signifikante Unterschiede auf. Bei amorphen Kunststoffen findet die plastische Deformation im Glaszustand statt. Hier bewirken lokale molekulare Bewegungsprozesse unter der Einwirkung der Spannung die Bildung plastizierter Mikrodomänen, deren Wachstum und Vereinigung makroskopisch zur plastischen Deformation in Form von Scherbändern oder Crazes führen [4, 5]. Bei teilkristallinen Kunststoffen findet die plastische Deformation i. Allg. oberhalb der Glastemperatur in den amorphen Bereichen statt. Hier stellen kristallographische Gleitprozesse den entscheidenden Deformationsschritt dar [6‒8] in dessen Ergebnis die lamellare Ausgangsstruktur in eine Fibrillenstruktur überführt wird [9, 10]. Aus der Betrachtung der Deformationsmechanismen wird deutlich, dass die mikroskopischen Prozesse, die zur plastischen Deformation führen, bereits weit unterhalb der Fließgrenze einsetzen. Häufig lassen sie sich schon bei einer Beanspruchung im linear-viskoelastischen Bereich nachweisen, so dass Zusammenhänge zwischen Relaxationszeitspektrum und plastischem Verhalten hergestellt werden können [11].
Im Ergebnis der plastischen Deformation findet eine Orientierung der Makromoleküle statt. Die damit verbundenen Eigenschaftsänderungen sind Ziel zahlreicher Verarbeitungsprozesse. Durch die molekulare Orientierung werden entropieelastische Rückstellkräfte (siehe Entropieelastizität) hervorgerufen, die der plastischen Deformation entgegenwirken und Ursache für die bei großen Verformungen zu beobachtenden Verfestigungsprozesse sind. Bei weiterer Steigerung der Beanspruchung kommt es zum lokalen Bruch überlasteter Polymerketten, der dem makroskopischen Versagen oder Bruch des Materials vorausgeht.
Siehe auch
- Deformationsmechanismen
- Energieelastizität
- Entropieelastizität
- Crazing
- Brucharten
- Zugversuch Ereignisbezogene Interpretation
- Scherbandbildung
Literaturhinweise
| [1] | Grellmann, W., Seidler, S. (Hrsg.): Kunststoffprüfung. Carl Hanser Verlag, München (2024) 4. Auflage, S. 90–92 (ISBN 978-3-446-44718-9; E-Book: ISBN 978-3-446-48105-3; siehe AMK-Büchersammlung unter A 23) |
| [2] | G’Sell, C., Jonas, J. J.: Determination of the Plastic Behaviour of Solid Polymers at Constant True Strain Rate. J. Mater. Sci. 14 (1979) 583‒591 |
| [3] | Ward, I. M.: Review: The Yield Behavior of Polymers. J. Mater. Sci. 6 (1971) 1397‒1417 |
| [4] | Argon, A. S.: A Theory for the Low-temperature Plastic Deformation of Glassy Polymers. Philos. Mag. 28 (1973) 839‒865 |
| [5] | Perez, J.: Physics and Mechanics of Amorphous Polymers. A. A. Balkema Verlag, Rotterdam (1998) (e-Book ISBN 978-0-2037-4333-1) |
| [6] | Bowden, P. B., Young, R. J.: Deformation Mechanisms in Crystalline Polymers. J. Mater. Sci. 9 (1974) 2034‒2051 |
| [7] | Lin, L., Argon, A. S.: Structure and Plastic Deformation of Polyethylene. J. Mater. Sci. 29 (1994) 294‒323 |
| [8] | Christ, B.: Plastic Deformation of Polymers. In: Thomas, E. I. (Ed.): Materials Science and Technology, Vol. 12: Structure and Properties of Polymers. Wiley VCH Verlag, Weinheim (2002) (ISBN 978-3-52726825-2) |
| [9] | Peterlin, A.: Plastic Deformation of Polyethylene by Rolling and Drawing. Kolloid Z. u. Z.: Polymer 233 (1969) 857‒862 |
| [10] | Petermann, J., Kluge, W., Gleiter, H.: Electron Microscopic Investigation of the Molecular Mechanism of Plastic Deformation of Polyethylene and Isotactic Polystyrene Crystals. Polym. Sci. B-Polym. Phys. 17 (1979) 1043‒1051 |
| [11] | Bauwens-Crowett, C., Bauwens, C. J., Homes, G.: Tensile Yield Stress Behavior of Glassy Polymers. J. Polym. Sci. A-2-Polym. Chem. 7 (1969) 735‒742 |