Zugfestigkeit
| Ein Service der |
|---|

|
| Polymer Service GmbH Merseburg |
| Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de |
| Unser Weiterbildungsangebot: https://www.psm-merseburg.de/weiterbildung |
| PSM bei Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg |
Zugfestigkeit
Zugfestigkeit
Im konventionellen Zugversuch an Kunststoffen werden spannungs- und dehnungsbezogene Kennwerte nach DIN EN ISO 527-1 ermittelt, wobei die Kenngrößen ausgewählten Punkten des Spannungs-Dehnungs-Diagramms entsprechen. Definitionsgemäß entspricht die Zugfestigkeit σm oder σM dem Spannungswert auf der vertikalen Achse des σ-ε-Diagramms bei dem ersten Spannungsmaximum während des Zugversuchs und berechnet sich nach Gl. (1) [1].
| (1) |
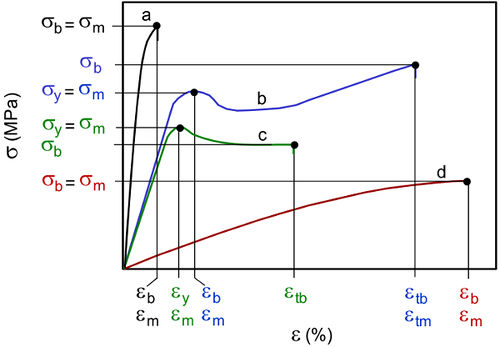
Je nach Diagrammtyp (a bis d) des untersuchten Kunststoffes kann die Zugfestigkeit σm identisch mit der Streckspannung σy oder der Bruchspannung σb sein (Bild 1). Obwohl der Bruchspannung als Kenngröße in der Norm angegeben ist, sollte dieser Wert nicht als Vergleichsgröße von Kunststoffen benutzt werden, da dieser sehr stark von dem Abschaltkriterium der Materialprüfmaschine abhängt.
Dehnung bei Zugfestigkeit und Bruchdehnung
Der zugehörige Kennwert auf der horizontalen Achse markiert den Ort des Auftretens des ersten Maximums und wird als Dehnung der Zugfestigkeit oder besser Dehnung bei der Zugfestigkeit εm bezeichnet. Dieser Kennwert kann ebenfalls mit der Streckdehnung εy oder der Bruchdehnung εb übereinstimmen. Prinzipiell muss die Dehnung bis zur Streckgrenze εy (Diagramme b und c in Bild 1) mit Dehnmessfühlern als normativer Wert gemessen werden oder bei Diagrammen ohne Streckgrenze bis zum Bruch (Diagramme a und d in Bild 1) auch mittels Ansetzdehnungsaufnehmern (siehe: Zugversuch, Wegmesstechnik) bestimmt werden.
| (2) |
| Bild 1: | Typische Spannungs-Dehnungs-Kurven und zugehörige Kenngrößen im Zugversuch [1] |
Die Kennwerte Bruchdehnung oder Dehnung bei der Zugfestigkeit werden bei den Diagrammtypen b und c aus der Summe der normativen Dehnung bis zur Streckgrenze und der nachfolgenden nominellen Dehnung aus dem Traversenweg nach Gl. (2) ermittelt. L ist dabei der Klemmenabstand und Lt entspricht der Verlängerrung ΔL bzw. der Vergrößerung des Abstands zwischen den Einspannklemmen. Die normative Dehnung, die immer als direkt am Prüfkörper gemessene Verformung ermittelt wird, wird nach Gl. (3) berechnet. L0 ist dabei der Initialabstand des Dehnmessfühlers am Prüfkörper und ΔL0 ist die gemessene Verlängerung des Fühlerabstands. Die Dehnung kann dimensionslos (Gln. 2 und 3) oder bei Multiplikation mit dem Faktor 100 in Prozent angegeben werden.
| (3) |
Spannungs-Dehungs-Diagramm für PA6
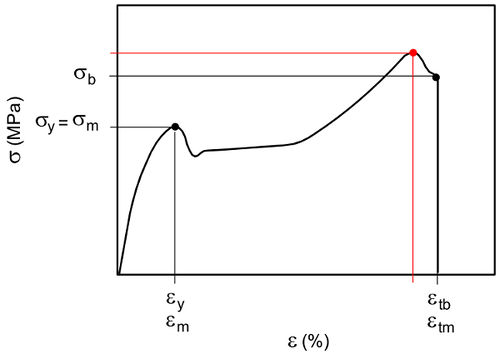
Die Auswertung entsprechend der Norm [1] gestaltet sich schwierig, wenn ein Spannungs-Dehnungs-Diagramm im Zugversuch z. B. für PA 6 entsprechend dem Bild 2 ermittelt wird. Aufgrund der Definition, dass die Zugfestigkeit dem ersten Spannungsmaximum entspricht, kann das absolute Maximum nach dieser Norm mit keiner Kenngröße belegt werden, da alle Kenngrößen schon vergeben sind. Im Gegensatz zu üblichen Auswerteprozedur der Prüfmaschinenhersteller und einer Vorgängerrevision dieser Norm [2] wird hier das absolute Maximum als Zugfestigkeit σm und das relative Maximum nur als Streckspannung σy bezeichnet. Die Definition der Zugfestigkeit lautete hier, dass dies die Maximalspannung ist, die der Prüfkörper während des Zugversuchs erträgt.
| Bild 2: | Nominelle und normative Dehnrate eines Prüfkörpers im Zugversuch |
Die Zugfestigkeit hängt sehr stark von der Prüfgeschwindigkeit und der Prüftemperatur ab und ist nur unter identischen Prüfbedingungen und Prüfkörpern für verschiedene Werkstoffe vergleichbar.
Eine umfassende Literaturanalyse zu den mechanischen Kennwerten des Zugversuchs Et, σM und εB ist für zahlreiche Kunststoffe in [3] zusammengestellt.
Siehe auch
- Festigkeit
- TABOR-Beziehung
- Zugversuch Überlagerung Kriechen Relaxation
- Zugversuch Gleichmaßdehnung
- Zugversuch Eigenspannungen Orientierungen
Literaturhinweise
| [1] | DIN EN ISO 527-1 (2019-12): Kunststoffe – Bestimmung der Zugeigenschaften – Teil 1: Allgemeine Grundsätze |
| [2] | DIN EN ISO 527-1 (1996-04): Kunststoffe – Bestimmung der Zugeigenschaften – Teil 1: Allgemeine Grundsätze |
| [3] | Bierögel, C., Grellmann, W.: Quasi-Static Tensile Test. In: Grellmann, W., Seidler, S.: Mechanical and Thermomechanical Properties of Polymers. Landolt-Börnstein, Volume VIII/6A3, Springer Verlag, Berlin (2014) 76–143, (ISBN 978-3-642-55165-9; siehe AMK-Büchersammlung unter A 16) DOI: http://dx.doi.org/10.1007/978-3-642-55166-6_16 |