Pure Shear-Prüfkörper
| Ein Service der |
|---|

|
| Polymer Service GmbH Merseburg |
| Tel.: +49 3461 30889-50 E-Mail: info@psm-merseburg.de Web: https://www.psm-merseburg.de |
| Unser Weiterbildungsangebot: https://www.psm-merseburg.de/weiterbildung |
| PSM bei Wikipedia: https://de.wikipedia.org/wiki/Polymer Service Merseburg |
Pure Shear-Prüfkörper
Prüfkörperformen für die Elastomerprüfung
Der Pure Shear-Prüfkörper wird neben dem Single-Edge-Notched Band (SENB-Prüfkörper) und dem Trousersprüfkörper zur Bestimmung bruchmechanischer Kennwerte (siehe: Bruchmechanische Prüfung) von Elastomer-Werkstoffen eingesetzt [1‒4].
Die Anwendung der Konzepte der Bruchmechanik für die Charakterisierung des Deformations- und Bruchverhaltens von Elastomeren ist mit grundlegenden Schwierigkeiten verbunden, da Elastomere weder ein linear-elastisches, noch ein elastisch-plastisches Werkstoffverhalten aufweisen. Außerdem ist die Deformation nicht auf den Bereich vor und um die Rissspitze beschränkt und auch hochdeformierte Risse bleiben nicht scharf wie beim GRIFFITH-Modell. Es gibt keine Energiedissipation durch Plastizität und die Bruchprozesse sind spröd [5].
Reißenergie von Elastomeren nach RIVLIN und THOMAS
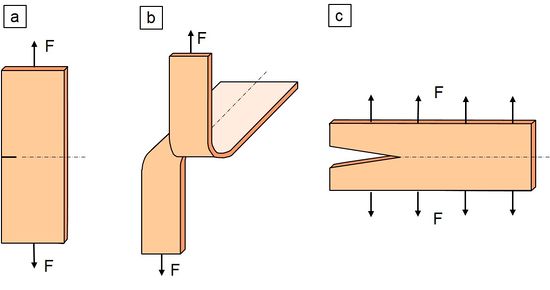
In der fundamentalen Arbeit von Rivlin und Thomas [6] wird die Reißenergie oder englisch Tearing Energy T mit Hilfe von Gl. (1) als bruchmechanische Kenngröße für Elastomere eingeführt und für die verschiedenen Prüfkörpergeometrien (siehe Bild 1) die Bestimmungsgleichungen Gln. (2) bis (4) abgeleitet.
| (1) |
| Bild 1: | Prüfkörperformen (a) SENT, (b) Trousers und (c) Pure Shear zur Ermittlung der Reißenergie T nach Rivlin und Thomas [6] |
| (2) |
| (3) |
- Pure Shear-Prüfkörper:
| (4) |
mit:
| k (λ) = π/ λ1/2 |
| λ = l/l0, |
| l – Verlängerung |
| l0 – Messlänge |
| W0 – Dehnungsenergiedichte und |
| a – Anfangsrisslänge |
SENT-Prüfkörper haben den Vorteil, dass sie relativ einfach durch Ausstanzen herstellbar sind und im Vergleich zum Pure Shear-Prüfkörper mit einem geringeren Materialeinsatz verbunden sind. Trousersprüfkörper sind aufgrund der Tatsache, dass sie auch für die Durchführung des konventionellen Weiterreißversuches verwendet werden können, auch relativ verbreitet für die Ermittlung bruchmechanischer Kennwerte [7–9]. Es ist bei der Verwendung von Trousersprüfkörpern zu berücksichtigen, dass der Spannungszustand vor der Rissspitze im Vergleich zum SENT- und Pure Shear-Prüfkörper sehr komplex ist. Darüber hinaus muss sichergestellt werden, dass sämtliche äußere Verformungsenergie nur für die Erweiterung des Risses aufgewendet wird, das heißt, es darf keine ausgeprägte elastische Deformation des Prüfkörpers stattfinden. Oftmals wird Gc bzw. T für den Fall der Verwendung von Trousersprüfkörpern nach folgender Gl. (5) bestimmt:
| (5) |
Tritt elastische Deformation auf, muss zur Berechnung eines bruchmechanischen Kennwertes Gl. (3) verwendet werden (siehe Bruchmechanik). Da jedoch die elastische Deformation von bestimmten Bereichen des Prüfkörpers nicht ausgeschlossen werden kann, sollte Gl. (5) nur für eine Abschätzung der Energiefreisetzungsrate G oder der Reißenergie T herangezogen werden und weiterhin sollten SENT- oder Pure Shear-Prüfkörper bevorzugt werden.
Einsatz von Pure Shear-Prüfkörpern für die Aufnahme von Risswiderstands(R)-Kurven
Der Vorteil des Pure Shear-Prüfkörpers liegt in der Unabhängigkeit der damit ermittelbaren Reißenergie T von der Risslänge (Gl. 4). Das bedeutet, auch während eines kontinuierlich während der Beanspruchung wachsenden Risses ist die risslängenunabhängige Bestimmung von T möglich. Dies ist insbesondere im Hinblick auf die Durchführung dynamischer Experimente interessant, aber auch für die Ermittlung von Risswiderstandskurven unter Anwendung der Einprobentechnik. Nachteilig im Vergleich zum SENT-Prüfkörper ist die experimentelle Durchführung der bruchmechanischen Experimente im Hinblick auf die Einspannung der Pure Shear-Prüfkörper. Insbesondere sehr zähe und steife Elastomerwerkstoffe wie z. B. rußverstärkte NR-Vulkanisate benötigen besondere Lösungen bei der Einspannung von breiten Pure Shear-Prüfkörpern. Werden hier lediglich plane Prüfkörper verwendet, kann es dann leicht zu Rutscheffekten des Prüfkörpers in den Einspannklemmen und damit zu einer unzulässigen Beeinflussung der Ergebnisse kommen. Das ist anschaulich in Bild 2 dargestellt, welches Aufnahmen eines Prüfkörpers während einer kontinuierlich ansteigenden quasistatischen Belastung zeigt.
| Bild 2: | Zunehmende Beanspruchung eines Pure Shear-Prüfkörpers aus einem mit 40 phr Ruß verstärkten NR-Vulkanisat während eines quasistatischen Bruchmechanikversuches mit finalem Klemmenrutschen |
Bei hohen Spannungen wurde hier ein Klemmenrutschen des Prüfkörpers (siehe: Prüfkörpereinspannung) beobachtet. Dem kann z. B. durch die Verwendung von Prüfkörpern mit Wulst entgegengewirkt werden, was aber gleichzeitig einen erhöhten Aufwand bei der Herstellung der Prüfkörper bedeutet, da ein einfaches Ausstanzen aus ebenem Plattenmaterial nicht möglich ist. Es müssen spezielle Pressformen vorhanden sein, um derartige Prüfkörper direkt vulkanisieren zu können. Weiterhin ist zu beachten, dass der Pure Shear-Prüfkörper maximal so breit sein darf wie die Einspannklemme (siehe auch Prüfkörpereinspannung). Dies setzt wiederum eine passende Laborausstattung voraus. Auch der Aspekt der Einbringung sollte bei der Auswahl der geeigneten Prüfkörperform berücksichtigt werden (siehe auch Kerbgeometrie). Je größer der einzubringende Kerb ist, desto schwieriger ist es, die Kerbeinbringung mit einer Metallklinge zu realisieren. Für Pure Shear- und Trousersprüfkörper sollte demzufolge die Kerbeinbringung bereits bei der Probenherstellung erfolgen. Dann ist lediglich eine geringe Erweiterung dieses Kerbs um einen kleinen Metallklingenkerb erforderlich. Gleichzeitig werden damit aber auch die Variationsmöglichkeiten hinsichtlich des Verhältnisses von Anfangsrisslänge a0 zur Prüfkörperbreite W eingeschränkt.
Ermittlung bruchmechanischer Kenngrößen
Die Reißenergie basiert ebenso wie die Energiefreisetzungsrate und das J-Integral auf einer energetischen Interpretation des Reißvorgangs und ist als die zur Erzeugung einer neuen Oberfläche erforderliche Änderung der Verformungsenergie definiert. Aus diesem Grund sind diese drei Größen als formal identisch zu betrachten:
| (6) |
Eine Voraussetzung für die Gleichheit von J und T ist die Bestimmung von J unter konstanter Verschiebung [10]. Horst [11] machte allerdings deutlich, dass die Energiedissipation, die mit der Rissausbreitung in Elastomeren einhergeht, nicht nur auf die unmittelbare Nähe um die Spitze eines Risses beschränkt ist, sondern im gesamten Prüfkörper auftritt. Dieser Umstand ist bei der Charakterisierung des Rissfortschritts durch eine globale Energiebilanz zu beachten.
Für Werkstoffe, die nicht vernachlässigbare plastische Deformation aufweisen, wurden J-Auswertemethoden abgeleitet, die diese unterschiedlichen Deformationsanteile berücksichtigen [12, 13]. Darauf wird hier aber nicht weiter eingegangen, da die im Rahmen der vorliegenden Arbeit betrachteten Werkstoffe im Wesentlichen nichtlinear viskoelastisch (siehe: Elastizität) deformierende Werkstoffe sind. Eine experimentelle Ermittlung von J kann hier nach der einfachsten Bestimmungsgleichung Gl. (7) erfolgen.
| (7) |
mit:
| η – Geometriefunktion |
| A – Verformungsenergie |
| a0 – Anfangsrisslänge |
| W – Prüfkörperbreite |
Die Geometriefunktion η kann entweder für die gewählte Prüfkörperkonfiguration aus der Literatur entnommen oder durch Anwendung der Compliance-Methode experimentell ermittelt werden [2, 12‒16].
Die vielfältigen Anwendungsbereiche von Elastomerwerkstoffen resultieren auch in teilweise sehr komplexen Beanspruchungen der Bauteile während des Gebrauchs, die sowohl mechanischer als auch medialer oder thermischer Natur sein können. Insbesondere unter dem Aspekt der Alterung, die zwangsläufig im Lauf der Zeit eintritt, ist es erforderlich quantitative Struktur-Eigenschafts-Beziehungen zu kennen, um Aussagen z. B. zur (Rest-) Lebensdauer machen zu können. Da Bauteile häufig durch die Bildung und Ausbreitung von Rissen versagen, kommt der quantitativen Charakterisierung des Risswiderstandes eine große ökonomische Bedeutung zu. Hier ist die Anwendung der bruchmechanischen Prüfung, basierend auf den oben erwähnten Konzepten, unerlässlich. Bruchmechanische Kenngrößen sind besonders struktursensitiv und demnach hervorragend für die Aufstellung von Struktur-Eigenschafts-Korrelationen geeignet. Bei der experimentellen Bestimmung bruchmechanischer Kennwerte muss berücksichtigt werden, dass eine Geometrieunabhängigkeit nur dann vorliegt, wenn im Prüfkörper ein ebener Dehnungszustand vorliegt, woraus sich jeweils bestimmte Anforderungen an die Prüfkörpergeometrie ableiten [12, 16] (siehe Geometriekriterium).
Literaturhinweise
| [1] | Reincke, K.: Elastomere Werkstoffe – Zusammenhang zwischen Mischungsrezeptur, Struktur und mechanischen Eigenschaften sowie dem Deformations- und Bruchverhalten, Habilitation, Martin-Luther-Universität Halle-Wittenberg, Shaker Verlag (2016), (ISBN 978-3-8440-4637-3; siehe AMK-Büchersammlung unter B 2-2) |
| [2] | Grellmann, W., Heinrich, G., Kaliske, M., Klüppel, M., Schneider, K., Vilgis, T. (Eds.): Fracture Mechanics and Statistical Mechanics of Reinforced Elastomeric Blends. Springer Verlag, Berlin, Heidelberg (2013), (ISBN 978‐3‐642‐37909‐3; siehe AMK-Büchersammlung unter A 14) |
| [3] | Stoček, R., Heinrich, G., Gehde, M.: The Influence of the Test Properties on Dynamic Crack Propagation in Filled Rubbers by Simultaneous Tensile‐ and Pure‐shear‐mode Testing. In: Heinrich, G., Kaliske, M., Lion, A., Reese, S., (Eds.): Constitutive Models for Rubber VI, CRC Press (2009) 345–352 |
| [4] | Stoček, R.: Dynamische Rissausbreitung in Elastomerwerkstoffen. Dissertation, Technische Universität Chemnitz (2012) |
| [5] | Bathias, C., LeGorja, K., Lu, C., Menabeuf, L.: Fatigue Crack Growth Damage in Elastomeric Materials. Fatigue and Fracture Mechanics: 27th Volume, ASTM STP 1296, R. S. Piascik, J. C. Newman, Dowling, N. E. (Eds.) American Society for Testing and Materials (1997) 505–513 |
| [6] | Rivlin, R. S., Thomas, A. G.: Rupture of Rubber. I. Characteristic Energy for Tearing. J. Polym. Sci. 10 (1953) 291–318 |
| [7] | Bhowmick, A. K., Gent A. N., Pulford, C. T. R.: Tear Strength of Elastomers under Threshold Conditions. Rubb. Chem. Techn. 56 (1983) 226 |
| [8] | Choudhury, N. R., Bhowmick, A. K.: Strength of Thermoplastic Elastomers from Rubber-polyolefin Blends. J. Mater. Sci. 25 (1990) 161–167 |
| [9] | Fukahori, Y., Sakulkaew, K., Busfield, J. J. C.: Elastic-viscous Transition in Tear Fracture of Rubbers. Polymer 54 (2013) 1905–1915 |
| [10] | Tsunoda, K., Busfield, J. J. C., Davies, C. K. L., Thomas, A. G.: Effect of Materials Variables on the Tear Behaviour of a Non-crystallising Elastomer. J. Mat. Sci. 35 (2000) 5187–5198 |
| [11] | Horst, T.: Spezifische Ansätze zur bruchmechanischen Charakterisierung von Elastomeren, Dissertation, Technische Universität Dresden (2011) (ISBN 978-3-942710-33-6; siehe AMK-Büchersammlung unter K 11) |
| [12] | Grellmann, W., Seidler, S. (Hrsg.): Kunststoffprüfung. 3. Auflage, Carl Hanser Verlag, München (2015), (ISBN 978-3-446-44350-1; siehe AMK-Büchersammlung unter A 18) |
| [13] | Standard Draft ESIS TC 4 (2001): A Testing Protocol for Conducting J‐Crack Growth Resistance Curve Tests on Plastics |
| [14] | Blumenauer, H.; Pusch, G., Technische Bruchmechanik. Deutscher Verlag für Grundstoffindustrie, Leipzig, Stuttgart (1993), (ISBN 3-342-06659-5; siehe AMK-Büchersammlung unter E 29-3) |
| [15] | Anderson, T. L.: Fracture Mechanics – Fundamentals and Application. 3rd Ed., CRC Taylor & Francis, Boca Raton Ann Arbor London Tokyo (2005) (ISBN 978-0-8493-1656-2; siehe AMK-Büchersammlung unter E 8-2) |
| [16] | Grellmann, W., Seidler, S. (Eds.): Deformation and Fracture Behaviour of Polymers. Springer Verlag, Berlin, Heidelberg (2001), (ISBN 978-3-540-41247-2; siehe AMK-Büchersammlung unter A 7) |